average_precision_score()函数----计算过程与原理详解

news2025/7/10 21:54:15

最近在复现论文时发现作者使用了 sklearn.metrics 库中的 average_precision_score() 函数用来对分类模型进行评价。

看了很多博文都未明白其原理与作用，看了sklean官方文档也未明白，直至在google上找到这篇文章Evaluating Object Detection Models Using Mean Average Precision (mAP)，才恍然大悟，现作简单翻译与记录。

文章目录

        • 从预测分数到类别标签(From Prediction Score to Class Label)
        • 精确度-召回度曲线(Precision-Recall Curve)
        • 平均精度AP(Average Precision)
      • 总结
        • 验证函数是否与该算法对照
        • 结语

首先先说明一下计算的过程：

  1. 使用模型生成预测分数。
  2. 通过使用阈值将预测分数转化为类别标签。
  3. 计算混淆矩阵。
  4. 计算对应的精确率和召回率。
  5. 创建精确率-召回率曲线。
  6. 计算平均精度。

接下来分为三个阶段讲解:

从预测分数到类别标签(From Prediction Score to Class Label)

在本节中，我们将快速回顾一下如何从预测分数中派生出类标签。

假设有两个类别，Positive 和 Negative，这里是 10 个样本的真实标签。

y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive"]

当这些样本被输入模型时，它会返回以下预测分数。基于这些分数，我们如何对样本进行分类（即为每个样本分配一个类标签）？

pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3]

为了将预测分数转换为类别标签，使用了一个阈值。当分数等于或高于阈值时，样本被归为一类(通常为正类, 1)。否则，它被归类为其他类别(通常为负类，0)。

以下代码块将分数转换为阈值为 0.5 的类标签。

import numpy

pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3]
y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive"]

threshold = 0.5
y_pred = ["positive" if score >= threshold else "negative" for score in pred_scores]
print(y_pred)

转化后的标签如下:

['positive', 'negative', 'positive', 'positive', 'positive', 'positive', 'negative', 'negative', 'negative', 'negative']

现在 y_true 和 y_pred 变量中都提供了真实标签和预测标签。

基于这些标签，可以计算出混淆矩阵、精确率和召回率。(可以看这篇博文，讲得很不错，不过混淆矩阵那个图有点小瑕疵)

r = numpy.flip(sklearn.metrics.confusion_matrix(y_true, y_pred))
print(r)

precision = sklearn.metrics.precision_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
print(precision)

recall = sklearn.metrics.recall_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
print(recall)

其结果为

# Confusion Matrix (From Left to Right & Top to Bottom: True Positive, False Negative, False Positive, True Negative)
[[4 2]
 [1 3]]

# Precision = 4/(4+1)
0.8

# Recall = 4/(4+2)
0.6666666666666666

在快速回顾了计算准确率和召回率之后，接下来我们将讨论创建准确率-召回率曲线。

精确度-召回度曲线(Precision-Recall Curve)

根据给出的精度precision和召回率recall的定义，请记住，精度越高，模型将样本分类为阳性时的置信度就越高。召回率越高，模型正确分类为 Positive 的正样本就越多。

当一个模型具有高召回率但低精度时，该模型正确分类了大部分正样本，但它有很多误报（即将许多负样本分类为正样本）。当一个模型具有高精确度但低召回率时，该模型将样本分类为 Positive 时是准确的，但它可能只分类了一些正样本。
注：本人理解，要想一个模型真正达到优秀的效果，精确率和召回率都应较高。

由于准确率和召回率的重要性，一条准确率-召回率曲线可以显示不同阈值的准确率和召回率值之间的权衡。该曲线有助于选择最佳阈值以最大化两个指标。

创建精确召回曲线需要一些输入：

1. 真实标签。
2. 样本的预测分数。
3. 将预测分数转换为类别标签的一些阈值。

下一个代码块创建 y_true 列表来保存真实标签，pred_scores 列表用于预测分数，最后是用于不同阈值的 thresholds 列表。

import numpy

y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive", "positive", "positive", "positive", "negative", "negative", "negative"]

pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3, 0.7, 0.5, 0.8, 0.2, 0.3, 0.35]

thresholds = numpy.arange(start=0.2, stop=0.7, step=0.05)

这是保存在阈值列表中的阈值。因为有 10 个阈值，所以将创建 10 个精度和召回值。

[0.2, 
 0.25, 
 0.3, 
 0.35, 
 0.4, 
 0.45, 
 0.5, 
 0.55, 
 0.6, 
 0.65]

下一个名为 precision_recall_curve() 的函数接收真实标签、预测分数和阈值。它返回两个代表精度和召回值的等长列表。

import sklearn.metrics

def precision_recall_curve(y_true, pred_scores, thresholds):
    precisions = []
    recalls = []
    
    for threshold in thresholds:
        y_pred = ["positive" if score >= threshold else "negative" for score in pred_scores]

        precision = sklearn.metrics.precision_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
        recall = sklearn.metrics.recall_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
        
        precisions.append(precision)
        recalls.append(recall)

    return precisions, recalls

以下代码在传递三个先前准备好的列表后调用 precision_recall_curve() 函数。它返回精度和召回列表，分别包含精度和召回的所有值。

precisions, recalls = precision_recall_curve(y_true=y_true, 
                                             pred_scores=pred_scores,
                                             thresholds=thresholds)

以下是精度precision列表中的返回值

[0.5625,
 0.5714285714285714,
 0.5714285714285714,
 0.6363636363636364,
 0.7,
 0.875,
 0.875,
 1.0,
 1.0,
 1.0]

这是召回recall列表中的值列表

[1.0,
 0.8888888888888888,
 0.8888888888888888,
 0.7777777777777778,
 0.7777777777777778,
 0.7777777777777778,
 0.7777777777777778,
 0.6666666666666666,
 0.5555555555555556,
 0.4444444444444444]

给定两个长度相等的列表，可以在二维图中绘制它们的值，如下所示

matplotlib.pyplot.plot(recalls, precisions, linewidth=4, color="red")
matplotlib.pyplot.xlabel("Recall", fontsize=12, fontweight='bold')
matplotlib.pyplot.ylabel("Precision", fontsize=12, fontweight='bold')
matplotlib.pyplot.title("Precision-Recall Curve", fontsize=15, fontweight="bold")
matplotlib.pyplot.show()

准确率-召回率曲线如下图所示。请注意，随着召回率的增加，精度会降低。原因是当正样本数量增加（高召回率）时，正确分类每个样本的准确率降低（低精度）。这是预料之中的，因为当有很多样本时，模型更有可能失败。
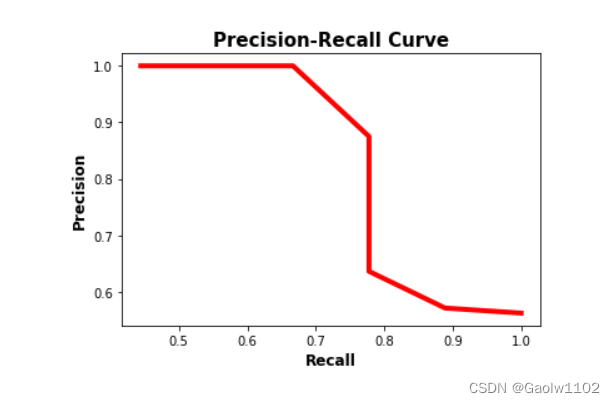
在这里插入图片描述

准确率-召回率曲线可以很容易地确定准确率和召回率都高的点。根据上图，最好的点是(recall, precision)=(0.778, 0.875)。

使用上图以图形方式确定精度和召回率的最佳值可能有效，因为曲线并不复杂。更好的方法是使用称为 f1 分数(f1-score) 的指标，它是根据下一个等式计算的。
在这里插入图片描述
f1 指标衡量准确率和召回率之间的平衡。当 f1 的值很高时，这意味着精度和召回率都很高。较低的 f1 分数意味着精确度和召回率之间的失衡更大。

根据前面的例子，f1是根据下面的代码计算出来的。根据 f1 列表中的值，最高分是 0.82352941。它是列表中的第 6 个元素（即索引 5）。召回率和精度列表中的第 6 个元素分别为 0.778 和 0.875。对应的阈值为0.45。

f1 = 2 * ((numpy.array(precisions) * numpy.array(recalls)) / (numpy.array(precisions) + numpy.array(recalls)))

结果如下

[0.72, 
 0.69565217, 
 0.69565217, 
 0.7,
 0.73684211,
 0.82352941, 
 0.82352941, 
 0.8, 
 0.71428571, 
 0.61538462]

下图以蓝色显示了与召回率和准确率之间的最佳平衡相对应的点的位置。总之，平衡精度和召回率的最佳阈值是 0.45，此时精度为 0.875，召回率为 0.778。

matplotlib.pyplot.plot(recalls, precisions, linewidth=4, color="red", zorder=0)
matplotlib.pyplot.scatter(recalls[5], precisions[5], zorder=1, linewidth=6)

matplotlib.pyplot.xlabel("Recall", fontsize=12, fontweight='bold')
matplotlib.pyplot.ylabel("Precision", fontsize=12, fontweight='bold')
matplotlib.pyplot.title("Precision-Recall Curve", fontsize=15, fontweight="bold")
matplotlib.pyplot.show()

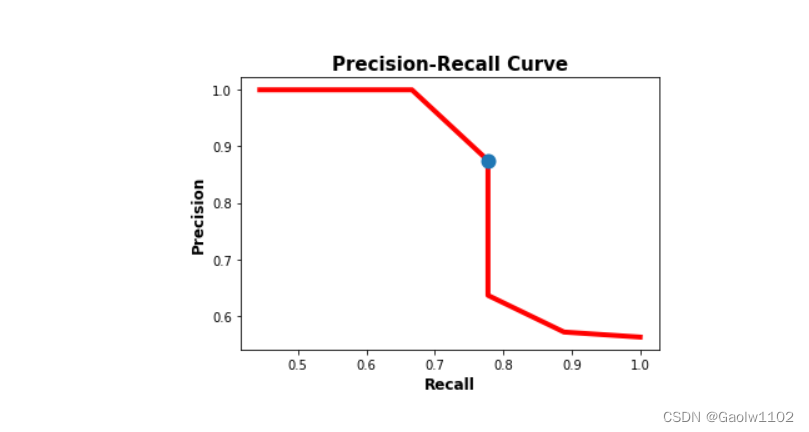
在这里插入图片描述
在讨论了精度-召回曲线之后，接下来讨论如何计算平均精度。

平均精度AP(Average Precision)

平均精度（AP）是一种将精度-召回曲线总结为代表所有精度平均值的单一数值的方法。 AP是根据下面的公式计算的。使用一个循环，通过遍历所有的精度precision/召回recall，计算出当前召回和下一次召回之间的差异，然后乘以当前精度。换句话说，Average-Precision是每个阈值的精确度(precision)的加权求和，其中的权重是召回率(recall)的差。

在这里插入图片描述
重要的是，要将召回列表recalls和精确列表precisions分别附加上0和1。例如，如果recalls列表是
0.8 , 0.6 0.8, 0.6 0.8,0.6
为它追加上 0， 就是
0.8 , 0.6 , 0.0 0.8, 0.6, 0.0 0.8,0.6,0.0
同样的，在精度列表precsion中附加1，
0.8 , 0.2 , 1.0 0.8, 0.2, 1.0 0.8,0.2,1.0
鉴于recalls和precisions都是NumPy数组，以上方程根据以下公式执行

AP = numpy.sum((recalls[:-1] - recalls[1:]) * precisions[:-1])

下面是计算AP的完整代码

import numpy
import sklearn.metrics

def precision_recall_curve(y_true, pred_scores, thresholds):
    precisions = []
    recalls = []
    
    for threshold in thresholds:
        y_pred = ["positive" if score >= threshold else "negative" for score in pred_scores]

        precision = sklearn.metrics.precision_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
        recall = sklearn.metrics.recall_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
        
        precisions.append(precision)
        recalls.append(recall**

    return precisions, recalls

y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive", "positive", "positive", "positive", "negative", "negative", "negative"]
pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3, 0.7, 0.5, 0.8, 0.2, 0.3, 0.35]
thresholds=numpy.arange(start=0.2, stop=0.7, step=0.05)

precisions, recalls = precision_recall_curve(y_true=y_true, 
                                             pred_scores=pred_scores, 
                                             thresholds=thresholds)

precisions.append(1)
recalls.append(0)

precisions = numpy.array(precisions)
recalls = numpy.array(recalls)

AP = numpy.sum((recalls[:-1] - recalls[1:]) * precisions[:-1])
print(AP)

总结

需要注意的是，在 average_precision_score() 函数中，做了一些算法上的调整，与上不同，会将每一个预测分数作为阈值计算对应的精确率precision和召回率recall。最后在长度为 len(预测分数) 的precisions和recalls列表上，应用 Average-Precision 公式，得到最终 Average-Precision 值。

验证函数是否与该算法对照

现在从sklean的官方文档中，得到该函数的使用用例，如下(官方链接)
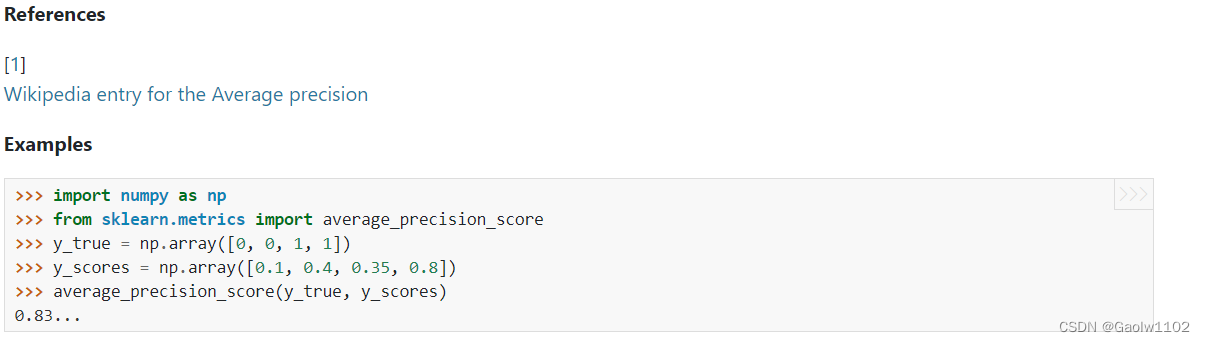
在这里插入图片描述
现在用以上的算法思想计算

import sklearn.metrics

'''
计算在给定阈值thresholds下的所有精确率与召回率
'''
def precision_recall_curve(y_true, pred_scores, thresholds):
    precisions = []
    recalls = []
    
    for threshold in thresholds:
        y_pred = [1 if score >= threshold else 0 for score in pred_scores]                           # 对此处稍微做修改
        print('y_true is:', y_true)
        print('y_pred is:', y_pred)
        
        confusion_matrix = sklearn.metrics.confusion_matrix(y_true, y_pred)                          # 输出混淆矩阵 
        precision = sklearn.metrics.precision_score(y_true=y_true, y_pred=y_pred)                    # 输出精确率
        recall = sklearn.metrics.recall_score(y_true=y_true, y_pred=y_pred)                          # 输出召回率
        
        print('confusion_matrix is:', confusion_matrix)
        print('precision is:', precision)
        print('recall is:', recall)
        
        precisions.append(precision)
        recalls.append(recall)                                                                       # 追加精确率与召回率
        
        print('\n')
        
    return precisions, recalls

计算每个阈值对应的精确率与召回率，最后得到precisions, recalls

precisions, recalls = precision_recall_curve([0, 0, 1, 1], [0.1, 0.4, 0.35, 0.8], [0.1, 0.4, 0.35, 0.8])

'''
结果
y_true is: [0, 0, 1, 1]
y_pred is: [1, 1, 1, 1]
confusion_matrix is: [[0 2] [0 2]]
precision is: 0.5
recall is: 1.0


y_true is: [0, 0, 1, 1]
y_pred is: [0, 1, 0, 1]
confusion_matrix is: [[1 1] [1 1]]
precision is: 0.5
recall is: 0.5


y_true is: [0, 0, 1, 1]
y_pred is: [0, 1, 1, 1]
confusion_matrix is: [[1 1] [0 2]]
precision is: 0.6666666666666666
recall is: 1.0


y_true is: [0, 0, 1, 1]
y_pred is: [0, 0, 0, 1]
confusion_matrix is: [[2 0] [1 1]]
precision is: 1.0
recall is: 0.5
'''

precisions列表与recalls列表分别追加1, 0，输出precisions列表与recalls列表

precisions.append(1), recalls.append(0)
precisions, recalls
'''
结果
([0.5, 0.5, 0.6666666666666666, 1.0, 1], [1.0, 0.5, 1.0, 0.5, 0])
'''

代入Average-Precision公式，得

在这里插入图片描述

avg_precision = 0                                         # 初始化结果为0

# 不断加权求和
for i in range(len(precisions)-1):
    avg_precision += precisions[i] * (recalls[i] - recalls[i+1])

print('avg_precision is:', avg_precision)                 # 输出结果

输出结果为

avg_precision is: 0.8333333333333333

可以看到，和sklearn.matrics.average_precision_score()算法的执行结果一致，故正确。

结语

以上内容均为认真查看资料并计算得出的，可能会存在不正确的地方，如有小伙伴存在异议，请留言评论！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/361938.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【SpringBoot 自动配置】-EnableAutoConfiguration 注解

【SpringBoot 自动配置】-EnableAutoConfiguration 注解

【SpringBoot 自动配置】-EnableAutoConfiguration 注解 续接上回 【Spring Boot 原理分析】- 自动配置 与【SpringBoot 自动配置】- Enable*注解 ,在前面笔者分析了在 SpringBoot 自动装配中的最重要的两个注解类， Condition 与 EnableAutoConfiguration 哎~说到…
阅读更多...
从0到1搭建大数据平台之监控

从0到1搭建大数据平台之监控

大家好，我是脚丫先生 (o^^o) 大数据平台设计中，监控系统尤为重要。 它时刻关乎大数据开发人员的幸福感。 试想如果半夜三更，被电话吵醒解决集群故障问题，那是多么的痛苦！！！ 但是不加班是不可…
阅读更多...
shiro总结

shiro总结

0x00 前言 此篇作为shiro总结篇，用于查漏补缺。 利用工具推荐：https://github.com/j1anFen/shiro_attack 0x01 反序列化 1.shiro 124 shiro 124，因为AES加密秘钥硬编码导致反序列化漏洞，124修复 Java 代码审计——shiro 1.2…
阅读更多...
React 虚拟DOM的前世今生

React 虚拟DOM的前世今生

引文 通过本文你将了解到 什么是虚拟DOM？虚拟DOM有什么优势？React的虚拟Dom是如何实现的？React是如何将虚拟Dom转变为真实Dom？ 一、前言 要了解虚拟DOM，我们先明确一下DOM的概念。 根据MDN的说法： 文档…
阅读更多...
Win10关闭自动更新

Win10关闭自动更新

Win10关闭自动更新第一步：修改电脑系统时间第二步，设置自动更新时间第三步：再次修改系统时间为正确时间因为国内使用的操作系统，很多‍是非正版的系统，如果更新了系统，很容易造成电脑蓝屏，系统运…
阅读更多...
90%的合同麻烦都源于签约“漏洞”，君子签电子签章闭坑指南来了！

90%的合同麻烦都源于签约“漏洞”，君子签电子签章闭坑指南来了！

业务签约中，有哪些合同麻烦呢？文字套路、印章造假、假冒代签、乱签漏签、信息泄露…事实上，这些签约“漏洞”都是源于签约风险排查不到位，管控不力而导致的，以至于后期履约中纠纷也不断。 君子签针对业务签约中的各类…
阅读更多...
小黑子的python入门到入土：第二章

小黑子的python入门到入土：第二章

python零基础入门到入土2.0python系列第二章1. 三目运算符2. 运算符优先级3. if 语句3.1 简单的if语句3.2 if-else 语句3.3 if-elif-else 语句3.4 if 语句注意点4. pass 关键字5. 猜拳游戏案例6. while 循环语句7. while 练习8. range9. for...in 循环的使用10. break 和contin…
阅读更多...
小林coding

小林coding

一、图解网络 问大家，为什么要有TCP/Ip网络模型？ 对于同一台设备上的进程通信，有很多种方式，比如有管道、消息队列、共享内存、信号等方式，对于不同设备上的进程通信，就需要有网络通信，而设备是…
阅读更多...
约束优化：PHR-ALM 增广拉格朗日函数法

约束优化：PHR-ALM 增广拉格朗日函数法

文章目录约束优化：PHR-ALM 增广拉格朗日函数法等式约束非凸优化问题的PHR-ALM不等式约束非凸优化问题的PHR-ALM对于一般非凸优化问题的PHR-ALM参考文献约束优化：PHR-ALM 增广拉格朗日函数法 基础预备： 约束优化：约束优化的三种序…
阅读更多...
【MyBatis】逆向工程与分页插件

【MyBatis】逆向工程与分页插件

11、MyBatis的逆向工程 11.1、创建逆向工程的步骤 正向工程：先创建Java实体类，由框架负责根据实体类生成数据库表。 Hibernate是支持正向工程的。 逆向工程：先创建数据库表，由框架负责根据数据库表，反向生成如下资源…
阅读更多...
公司技术团队为什么选择使用 YApi 作为 Api 管理平台？

公司技术团队为什么选择使用 YApi 作为 Api 管理平台？

在 2021 年 12 月份的时候我就推荐过一款软件程序员软件推荐：Apifox，当时体验了一下里面的功能确实很实用，但是当时公司有一套自己的 API 管理方案，所有 Apifox 暂时就没在内部使用。 直到最近要使用其他的 API 管理方案的时候才…
阅读更多...
SAP ERP系统PP模块MRP运行参数说明

SAP ERP系统PP模块MRP运行参数说明

SAP/PP模块运行MRP(MD01/MD02)的界面有很多参数，这些参数的设置上线前由PP业务顾问根据实际业务需求定义好的，上线后一般不会轻易去调整，对于一般操作用户，按手册操作就行，不需要深入了解这些参数，但作为负…
阅读更多...
收藏这几个开源管理系统做项目，领导看了直呼牛X！

收藏这几个开源管理系统做项目，领导看了直呼牛X！

项目SCUI Admin 中后台前端解决方案Vue .NetCore 前后端分离的快速发开框架next-admin 适配移动端、pc的后台模板django-vue-admin-pro 快速开发平台Admin.NET 通用管理平台RuoYi 若依权限管理系统Vue3.2 Element-Plus 后台管理框架Pig RABC权限管理系统zheng 分布式敏捷开发…
阅读更多...
Redis的下载与安装

Redis的下载与安装

为便于大多数读者学习本套教程，教程中采用 Windows 系统对 Redis 数据库进行讲解。虽然 Redis 官方网站没有提供 Windows 版的安装包，但可以通过 GitHub 来下载 Windows 版 Redis 安装包，下载地址：点击前往。 注意：Win…
阅读更多...
企业级解决方案Redis

企业级解决方案Redis

缓存预热“宕机”服务器启动后迅速宕机1. 请求数量较高2. 主从之间数据吞吐量较大，数据同步操作频度较高解决方案前置准备工作：1. 日常例行统计数据访问记录，统计访问频度较高的热点数据2. 利用LRU数据删除策略，构建数据留存队列例…
阅读更多...
全链路压力测试

全链路压力测试

压力测试的目标： 探索线上系统流量承载极限，保障线上系统具备抗压能力 复制代码 如何做全链路压力测试： 全链路压力测试：整体步骤 容量洪峰 -》 容量评估 -》 问题发现 -》 容量规划 全链路压力测试：细化过程 整体目…
阅读更多...
Apache Shiro与Spring Security对比

Apache Shiro与Spring Security对比

Apache Shiro VS Spring Security 1.Spring Security 官方文档：https://spring.io/projects/spring-security#overview介绍： Spring Security是一个能够为基于Spring的企业应用系统提供声明式的安全访问控制解决方案的安全框架。它提供了一组可以在Spr…
阅读更多...
Java 基础(3)—synchornized 关键字简单理解

Java 基础(3)—synchornized 关键字简单理解

一、synchronized 修饰同步代码块 用 synchronized 修饰代码段作为同步锁，代码如下： public class LockDemo {public Object object new Object();public void show(){synchronized (object) {System.out.println(">>>>>>hell…
阅读更多...
java Spring aop多个增强类作用于同一个方法时，设置优先级

java Spring aop多个增强类作用于同一个方法时，设置优先级

我们先来模拟这种情况 我们先创建一个java项目 然后 引入Spring aop需要的基本依赖 然后 在src下创建一个包 我这里叫 Aop 在Aop包下创建一个类 叫 User 参考代码如下 package Aop;import org.springframework.stereotype.Component;Component public class User {public vo…
阅读更多...
Java-形参与返回值

Java-形参与返回值

Java学习之道-1 一、形参与返回值 平时在进行代码编写的时候大多都是以变量作为形参或者以某种数据类型比如int、String或者Boolean等等作为返回值，本次主要介绍以下三种作为形参与返回值的情况 1、类名作为形参与返回值 类名，顾名思义是定义的class类&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023