研究背景

复杂网络的重要节点是指相比网络其他节点而言，能够在更大程度上影响网络的结构与功能的一些特殊节点。

近年来，节点重要性（中心性）排序研究受到越来越广泛的关注，不仅因为其重大的理论研究意义，更因为其广泛的实际应用价值。由于应用领域极广，且不同类型的网络中节点的重要性评价方法各有侧重，学者们从不同的实际问题出发设计出各种各样的方法。

提前约定

一个网络的拓扑图记为 $G(V，E)$
V = { v 1 , v 2 , ⋅ ⋅ ⋅ , v n } V=\{v_1,v_2,···,v_n\} V={v1​,v2​,⋅⋅⋅,vn​} ：节点集合，$n$ 为节点数
E = { e 1 , e 2 , ⋅ ⋅ ⋅ , e m } E=\{e_1, e_2,···,e_m\} E={e1​,e2​,⋅⋅⋅,em​}：边的集合，$m$ 为边数

一个图的邻接矩阵为：${\mathbf{A}}_{n\times n}=(a_{ij})$

无向网络	有向网络
$$a_{ij}=\{\begin{array}{l}1,v_i\text{与}{v}_j\text{之间有连边}\\ 0,v_i\text{与}{v}_j\text{之间无连边}\end{array}$$	$$a_{ij}=\{\begin{array}{l}1,存在一条从v_i\text{到}{v}_j\text{的有向边}\\ 0,不存在一条从v_i\text{到}{v}_j\text{的有向边}\end{array}$$

特别的，一个含权图的邻接矩阵为：${\mathbf{W}}_{n\times n}=(w_{ij})$
$$w_{ij}=\{\begin{array}{l}\text{连边上的权值, }{v}_i\text{与}{v}_j\text{之间有连边}\\ 0,v_i\text{与}{v}_j\text{之间无连边}\end{array}$$
同时约定所有在网络中传播的信息、病毒、车流、人流、电流等统称为网络流。

网络中的一条路径是类似这样的一组节点和边的交替序列：$v_1$,$e_1$,$v_2$,$e_2$,···,$e_{n1}$,$v_n$, 其中 $v_i$，$v_{i+1}$ 是 $e_i$ 的两个端点。如果任意一对节点之间都存在一条路径使它们相连, 就称这个网络是连通的。

基于节点近邻的排序方法

度中心性（degree centrality, DC）

观点：一个节点的邻居数目越多，影响力就越大，就越重要。
刻画角度：节点的直接影响力

节点 $v_i$ 的度：$k_i={\sum }_j{a}_{ij}$，表示与 $v_i$ 直接相连的节点的数目。在有向网络中, 根据连边的方向不同, 节点的度有入度和出度之分。在含权网络中节点度又称为节点的强度(strength)，定义为与节点相连的边的权重之和。

节点 $v_i$ 的归一化度中心性指标为：$$DC(i)=\frac{k_i}{n-1}$$

优点：简单、直观、计算复杂度低等；在网络鲁棒性和脆弱性研究中表现较好
缺点：没有对节点周围的环境进行更深入细致地探讨，不够精确。

半局部中心性（semilocal centrality, SLC）

目的：为了权衡效率和效果

节点 $v_w$ 的两层邻居度：$N(w)$，表示从 $v_w$ 出发 2 步内可到达的邻居的数目。
节点 $v_j$ 的一阶邻居节点（出发 1 步可以到达）的集合：$\Gamma (j)$

节点 $v_i$ 的半局部中心性定义为：$$SLC(i)=\sum _{w\in \Gamma \left(i\right)}\sum _{j\in \Gamma \left(w\right)}N\left(j\right)$$
表示节点 $v_i$的所有二阶邻居（出发 2 步可以到达）的两层邻居度之和，其中一项二阶邻居 $j$ 的两层邻居度 $N(j)$ 如下图被红色阴影覆盖的节点总数：

可以看出，半局部中心性涉及了节点的四阶邻居信息。

k-壳分解法

考虑因素：节点在网络中的位置：越接近核心，影响力越大。

该方法将外围的节点层层剥去, 处于内层的节点拥有较高的影响力。
剥去第一层的具体过程如下：

1、把度为 1 的节点及其所连接的边都去掉
2、去掉剩下网络中度为1的节点，不断循环此操作，直到所剩的网络中没有度为 1 的节点为止。
此时，所有被去掉的节点组成一个层, 称为 1-壳 (记为 $k_s=1$)，如下图。

剥掉一层之后在剩下的网络中节点的度就叫该节点的剩余度。
剥去一层后继续剥壳，去掉网络中剩余度为 2 的节点, 重复这些操作, 直到网络中没有节点为止。

更广泛地，可定义初始度为 0 的孤立节点属于 0-壳，即 $k_s=0$.

优点：计算复杂度低, 在分析大规模网络的层级结构等方面有很多应用。
缺点：有很多不能发挥作用的场景；排序结果太过粗粒化；在网络分解时仅考虑剩余度的影响从而不合理。

基于路径排序的方法

在交通、通信、社交等网络中存在着一些度很小但是很重要的节点，这些节点是连接几个区域的“桥节点”，它们在交通流和信息包的传递中担任重要的角色。此时，刻画节点重要性就需要考察网络中节点对信息流的控制力，这种控制力往往与网络中的路径密切相关。

假设：网络中的信息流只经过最短路径传输

离心中心性 (Eccentricity, ECC)

节点 $v_i$ 与 $v_j$ 之间的最短路径长度，即最短距离：$d_{ij}$
节点 $v_i$ 的离心中心性为它与网络中所有节点的最短距离之中的最大值:$$ECC(i)=\underset{j}{\max }\left(d_{ij}\right)$$

网络直径：所有节点的最大离心中心性
网络半径：所有节点的最小离心中心性
中心节点：离心中心性值等于网络半径的节点。一个节点的离心中心性与网络半径越接近就越中心

缺点：极易受特殊值的影响

接近中心性 (closeness centrality, CC)

方法：通过计算节点与网络中其他所有节点的距离的平均值来消除特殊值的干扰。

对于有 $n$ 个节点的连通网络, 节点 $v_i$ 到网络中其他节点的平均最短距离：$d_i=\frac{1}{n-1}{\sum }_{j\ne i}{d}_{ij}$

$d_i$ 越小意味着节点 $v_i$ 更接近网络中的其他节点，于是节点 $v_i$ 的接近中心性为：$$CC\left(i\right)=\frac{1}{d_i}$$

Katz 中心性

Katz 中心性不仅考虑节点对之间的最短路径，还考虑它们之间的其他非最短路径。

假设节点 $v_i$ 与节点 $v_j$ 之间有 $p$ 步长，$l_{ij}^{(p)}$ 表示节点 $v_i$ 到节点 $v_j$ 经过长度为 $p$ 的路径的数目。显然，$\left(l_{ij}^{\left(2\right)}\right)={\sum }_k{a}_{ik}{a}_{kj}={\mathbf{A}}^2$，同理得到 ${\mathbf{A}}^3,{\mathbf{A}}^4...{\mathbf{A}}^p...$。

Katz 中心性认为短路径比长路径更加重要，它通过一个与路径长度相关的因子 $s^p(s\in (0,1),为一个固定参数)$ 对不同长度的路径加权。 便可以得到一个描述网络中任意节点对之间路径关系的矩阵：$\mathbf{K}=s\mathbf{A}+s^2{\mathbf{A}}^2+...+s^p{\mathbf{A}}^p+...$，其中，$\mathbf{I}$ 为单位矩阵。

一个节点 $v_j$ 的 Katz 中心性：$$Katz\left(j\right)=\sum _i{k}_{ij}$$

评价：时间复杂度高，主要用在规模不太大，环路比较少的网络中。

信息指标 (INF)

信息指标通过路径中传播的信息量来衡量节点重要性。

假定：信息在一条边上传递的时候存在一定的噪音，路径越长噪音就越大。把网络看成一个电阻网络，每条边的电阻记为 1。

.一条路径上的信息传输量等于该路径长度的倒数。

一对节点 $(v_i,v_j)$ 间传输的信息总量为他们之间所有路径上传送的信息量的总和，记为 $q_{ij}$。

在中学我们学过的电阻的两个公式：

串联：$R=R_1+R_2$
并联：$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$

将这两个公式运用到这里的电阻网络上，我们可以得到以两个节点 $v_i$ 和 $v_j$ 为端点的电阻值：$\frac{1}{q_{ij}}$。举个例子：

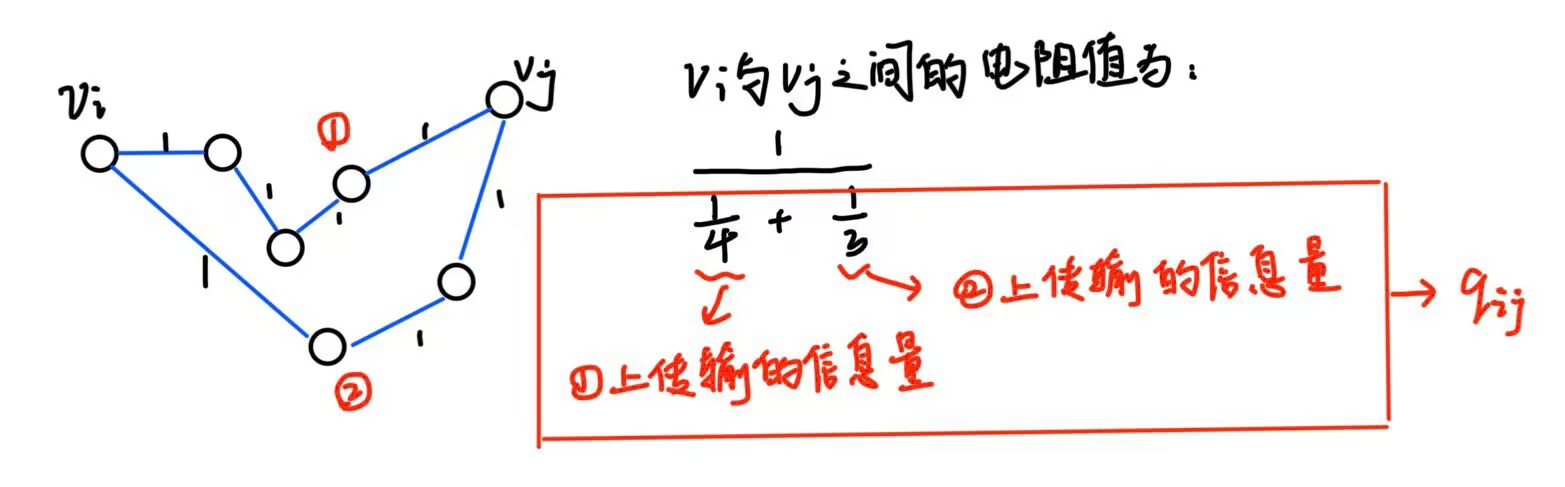
最后，用调和平均数的方法定义 $v_i$ 的中心性指标：$$INF(i)=[\frac{1}{n}\sum _j\frac{1}{q_{ij}}{]}^{-1}$$

优点：考虑了所有路径，并可通过电阻网络简化繁复的计算过程。该方法可以很容易地扩展到含权网络，也适用于非连通的网络。

介数中心性 (betweenness centrality, BC)

观点：经过一个节点的最短路径数越多，这个节点就越重要。

节点 $v_i$ 的介数表示在所有起点和终点都不是 $v_i$ 的最短路径中，经过 $v_i$ 的最短路径的比例，定义：$BC(i)={\sum }_{j\ne s,s\ne t,j\ne t}\frac{g_{st}^i}{g_{st}}$，其中 $g_{st}$ 表示从节点 $v_s$ 到节点 $v_t$ 所有路径的数目，$g_{st}^i$ 表示从节点 $v_s$ 到节点 $v_t$ 并经过 $v_i$ 的所有路径的数目。

包含 $n$ 个节点的连通网络的最大介数为包含 $n$ 个节点的星形网络中心节点的介数：$\frac{\left(n-1\right)\left(n-2\right)}{2}$，于是得到一个归一化的介数：$$B{C}^{\prime }\left(i\right)=\frac{2}{\left(n-1\right)\left(n-2\right)}\sum _{j\ne s,s\ne t,j\ne t}\frac{g_{st}^i}{g_{st}}$$

评价：计算时间复杂度较高，使其在实际应用中受到限制，可用于设计网络的通信协议、优化网络部署、检测网络瓶颈等。

流介数中心性 (flow betweenness centrality, FBC)

观点： 网络中所有不重复的路径中，经过一个节点的路径的比例越大，这个节点就越重要。

节点 $v_i$ 的流介数中心性：$$FBC\left(i\right)=\sum _{s<t}\frac{{\tilde{g}}_{st}^i}{{\tilde{g}}_{st}}$$

基于特征向量的排序方法

基于特征向量的方法不仅考虑节点邻居数量还考虑了其质量对节点重要性的影响。

特征向量中心性 (eigenvector centrality, EC)——适用于无向网络

观点：一个节点的重要性既取决于其邻居节点的数量（即该节点的度），也取决于每个邻居节点的重要性。

记 $x_i$ 为节点 $v_i$ 的重要性度量值，有：$$EC\left(i\right)=x_i=c\sum _{j=1}^n{a}_{ij}{x}_j$$

注：当节点 $v_i$ 与节点 $v_j$ 之间有边时，$a_{ij}=1$，否则$a_{ij}=0$

其中，$c$ 为一个比例常数，记 $\mathbf{x}=[x_1,x_2,x_3...x_n{]}^{\text{T}}$，经过多次迭代达到稳态后有：$$\mathbf{x}=c\mathbf{A}\mathbf{x}$$
从这里我们可以看出，$x$ 是矩阵 $\mathbf{A}$ 的特征值 $\frac{1}{c}$ 的特征向量。
计算向量 $x$ 的方法是：
1、给定初值 $x(0)$
2、采用迭代算法：$x(t)=c\mathbf{A}\mathbf{x}(t-1),t=1,2,\mathrm{3...}$
3、直到归一化的 $x^{\prime }(t)=x^{\prime }(t-1)$ 为止。

已有文献证明，为了使上述迭代过程收敛，使 $c=\frac{1}{\lambda }$，其中 $\lambda$ 为邻接矩阵 $\mathbf{A}$ 的主特征值（绝对值最大的特征值），即有：$$\mathbf{x}={\lambda }^{-1}\mathbf{A}\mathbf{x}$$

评价：特征向量中心性更加强调节点所处的周围环境，节点可以通过连接很多其他重要的节点来提升自身的重要性。 从传播的角度看，特征向量中心性适合于描述节点的长期影响力，如在疾病传播、谣言扩散中，一个节点的 EC 分值较大说明该节点距离传染源更近的可能性
越大，是需要防范的关键节点。

累计提名 (cumulative nomination)——适用于无向网络

为了使打分值能够收敛并且快速收敛，在每次迭代过程中，同时考虑邻居节点和自身的打分值。

节点 $v_i$ 在时刻 $t$ 时得到的提名次数：${\tilde{p}}_i^t$，假设 ${\tilde{p}}_i^0=1$。
每个时间步每个节点从所有相邻的节点处获得新增的提名，新增的提名数为邻居节点已有的提名数的总和。节点$v_i$ 在时刻 $t+1$ 的累积提名为：$${\tilde{p}}_i^{t+1}={\tilde{p}}_i^t+\sum _j{a}_{ij}{\tilde{p}}_j^t$$
将 ${\tilde{p}}_i^t$ 归一化得到：$p_i^t=\frac{{\tilde{p}}_i^t}{{\sum }_j{\tilde{p}}_j^t}$，如果所有节点归一化后的提名次数不再变化，则停止迭代。
稳态时每个节点的提名次数占所有节点的提名次数的比例就是其重要性权值。

PageRank 算法 (PR)——适用于有向网络

PageRank 算法基于网页的链接结构给网页排序，它认为万维网中一个页面的重要性取决于指向它的其他页面的数量和质量，如果一个页面被很多高质量页面指向，则这个页面的质量也高。

初始时刻：赋予每个节点（网页）相同的 PR 值
然后进行迭代：每一步把每个节点当前的 PR 值平分给它所指向的所有节点。

为什么时平分呢？我想可以这样理解：比如 A 指向了（引用了） B、C、D，A 的重要性包含有 B、C、D 的共同贡献，因此评分 PR 值也就将重要性对 B、C、D 进行了平分。

每个节点的新 PR 值为它所获得的 PR 值之和。节点 $v_i$ 在 $t$ 时刻的 PR 值为：$$P{R}_i\left(t\right)=\sum _{j=1}^n{a}_{ji}\frac{P{R}_j\left(t-i\right)}{k_j^{out}}$$

迭代直到每个节点的 PR 值都达到稳定时为止。

缺陷：PR 值一旦到达某个出度为零的节点（悬挂节点），就会永远停留在该节点处而无法传递出来，从而不断吸收 PR 值。

改进：引入一个随机跳转概率 $c$，每一步，不管一个节点是否为悬挂节点，其 PR 值都将以 $c$ 的概率均分给网络中所有节点，以 $1-c$ 的概率均分给它指向的节点。可得含参数 $c$ 的 PageRank 算法：$$P{R}_i\left(t\right)=\left(1-c\right)\sum _{j=1}^n{a}_{ji}\frac{P{R}_j\left(t-i\right)}{k_j^{out}}+\frac{c}{n}$$

❓ 我没有弄明白为什么公式后面是 $\frac{1}{n}$

参考文献