预积分和流形

论文：IMU Preintegration on Manifold for Effificient Visual-Inertial Maximum-a-Posteriori Estimation

引言

Recent results in monocular visual-inertial navigation (VIN) have shown that optimization-based approaches outperform filtering methods in terms of accuracy due to their capability to relinearize past states. However, the improvement comes at the cost of increased computational complexity. In this paper, we address this issue by preintegrating inertial measurements between selected keyframes. The preintegration allows us to accurately summarize hundreds of inertial measurements into a single relative motion constraint. Our first contribution is a preintegration theory that properly addresses the manifold structure of the rotation group and carefully deals with uncertainty propagation. The measurements are integrated in a local frame, which eliminates the need to repeat the integration when the linearization point changes while leaving the opportunity for belated bias corrections. The second contribution is to show that the preintegrated IMU model can be seamlessly integrated in a visual-inertial pipeline under the unifying framework of factor graphs. This enables the use of a structureless model for visual measurements, further accelerating the computation. The third contribution is an extensive evaluation of our monocular VIN pipeline: experimental results confirm that our system is very fast and demonstrates superior accuracy with respect to competitive state-of-the-art filtering and optimization algorithms, including off-the-shelf systems such as Google Tango [1].

引言

本文提出了一个使用增量平滑（incremental smoothing）快速计算最大后验估计(MAP)的系统。

第一项贡献是发展出了一种新颖的预积分理论。 预积分IMU测量的使用是在[26]中首次提出的，包括将两个关键帧之间的许多惯性测量组合成一个相对运动约束。 本文在此工作的基础上提出了一个预积分理论，该理论恰当地解决了旋转群的流形结构，并允许对所有雅可比矩阵进行解析推导。

[26]采用欧拉角作为旋转的全局参数化。Using Euler angles and applying the usual averaging and smoothing techniques of Euclidean spaces for state propagation and covariance estimation is not properly invariant under the action of rigid transformations [27]。 此外，已知欧拉角具有奇点。 在第五节中的理论推导也推进了之前[10,12,13,25]这些工作使用了预积分测量，但没有发展出不确定性传播和后验bias校正的相应理论。 本文受益于[26]开创性见解: 在局部坐标系中进行积分，当线性化点发生变化时不需要重复积分。

第二项贡献，我们将预积分的IMU模型框定为一个因子图视角（we frame our preintegrated IMU model into a factor graph perspective）。 这使得基于iSAM2 [24]的恒定时间VIN管道设计成为可能 。我们提出的增量平滑解决方案避免了线性化误差的积累，并提供了一个具有吸引力的替代方案，以使用自适应支持窗口进行优化[10]。

受[20,28]的启发，本文采用了一种无结构的视觉测量模型，该模型允许在增量平滑过程中消除大量变量(即所有3D点)，进一步加速计算。

第三个贡献是对系统进行了有效的实施和广泛的评估。 实验结果表明，后端需要平均10毫秒的CPU时间来计算full MAP估计，并与SOTA方法相比获得了更高的准确性。 论文附有补充材料[29]。 此外，本文在GTSAM 4.0优化工具箱中发布了IMU预积分和无结构视觉因子的实现 。

预备知识

黎曼几何记号

本节回顾与特殊正交群SO(3)和特殊欧氏群SE(3)相关的有用概念，基于[31,32]。

SO(3)

SO(3)描述了一组三维旋转矩阵，定义为 SO ( 3 ) ≡ { R ∈ R 3 × 3 : R T R = I , det ( R ) = 1 } \text{SO}(3) \equiv \{ \bold{R} \in \mathbb{R}^{3\times 3} : \bold{R}^{T} \bold{R} = \bold{I}, \text{det}(\bold{R}) = 1 \} SO(3)≡{R∈R3×3:RTR=I,det(R)=1} 。 群运算是一般的矩阵乘法，逆是矩阵转置。 SO(3)也形成光滑流形， 流形(在恒等处)的切空间（tangent space）表示为so(3)，这也称为李代数，并与3×3反对称矩阵的空间相一致。可以用hat符号在 ${\mathbb{R}}^3$ 中标识每个带有向量的反对称矩阵:
$${\mathbf{\omega }}^{\wedge }={\left[\begin{array}{l}{\omega }_1\\ {\omega }_2\\ {\omega }_3\end{array}\right]}^{\wedge }=\left[\begin{array}{ccc}0& -{\omega }_3& {\omega }_2\\ {\omega }_3& 0& -{\omega }_1\\ -{\omega }_2& {\omega }_1& 0\end{array}\right]\in \mathfrak{so}(3)\text{\hspace{1em}(1)}$$
可以用vee运算符将反对称矩阵映射到 ${\mathbb{R}}^3$ 中的向量：对于反对称矩阵 $\mathbf{S}={\mathbf{\omega }}^{\wedge }$ ，有： ${\mathbf{S}}^{\vee }=\mathbf{\omega }$ 。 反对称矩阵的一个性质是:
$${\mathbf{a}}^{\wedge }\mathbf{b}=-{\mathbf{b}}^{\wedge }\mathbf{a},\forall \mathbf{a},\mathbf{b}\in {\mathbb{R}}^3\text{\hspace{1em}(2)}$$

指数映射exp： $\text{so}(3)\to \text{SO}(3)$ 将一个李代数元素关联到一个旋转：
$$\exp \left({\varphi }^{\wedge }\right)=\mathbf{I}+\frac{\sin (\Vert \varphi \Vert )}{\Vert \varphi \Vert }{\varphi }^{\wedge }+\frac{1-\cos (\Vert \varphi \Vert )}{\Vert \varphi {\Vert }^2}{\left({\varphi }^{\wedge }\right)}^2\text{\hspace{1em}(3)}$$
指数映射的一阶近似为:
$$\exp \left({\varphi }^{\wedge }\right)\approx \mathbf{I}+{\varphi }^{\wedge }\text{\hspace{1em}(4)}$$

对数映射将一个SO(3)旋转矩阵关联到一个反对称矩阵：
$$\log (\mathrm{R})=\frac{\phi \cdot \left(\mathrm{R}-{\mathrm{R}}^{\top }\right)}{2\sin (\phi )}\text{ with }\phi ={\cos }^{-1}\left(\frac{\mathrm{tr}(\mathrm{R})-1}{2}\right)\text{\hspace{1em}(5)}$$
注意有 $\log (\mathbf{R}{)}^{\vee }=\mathbf{a}\phi$ ，$\mathbf{a}$ 是旋转轴， $\phi$ 是旋转角。

如果限制在开球 $\Vert \varphi \Vert <\pi$ ，指数映射是一个双射，对应的逆是对数映射。 然而，如果不限制定域，指数映射就会变成满射，因为每个向量 $\mathbf{\varphi }=(\phi +2k\pi )\mathbf{a},k\in \mathbb{Z}$ 都是R的一个对数。

为了便于标记，采用指数和对数映射的“向量化”版本:
$$\begin{array}{cccccccc}\mathrm{Exp}:& {\mathbb{R}}^3& \ni & \varphi & \to & \exp \left({\varphi }^{\wedge }\right)& \in & \mathrm{SO}(3)\\ \log :& \mathrm{SO}(3)& \ni & \mathrm{R}& \to & \log (R{)}^{\vee }& \in & {\mathbb{R}}^3\end{array}\text{\hspace{1em}(6)}$$
它们直接作用于向量，而不是so(3)。

使用以下一阶近似:
$$\mathrm{Exp}(\varphi +\delta \varphi )\approx \mathrm{Exp}(\mathbf{\varphi })\mathrm{Exp}\left({\mathrm{J}}_r(\mathbf{\varphi })\delta \mathbf{\varphi }\right)\text{\hspace{1em}(7)}$$
${\mathbf{J}}_r(\mathbf{\varphi })$ 是SO(3)的右雅可比，其将tangent空间中的加性增量与应用于右侧的乘法增量联系起来:
$${\mathrm{J}}_r(\varphi )=\mathbf{I}-\frac{1-\cos (\Vert \varphi \Vert )}{\Vert \varphi {\Vert }^2}{\varphi }^{\wedge }+\frac{\Vert \varphi \Vert -\sin (\Vert \varphi \Vert )}{\Vert {\varphi }^3\Vert }{\left({\varphi }^{\wedge }\right)}^2\text{\hspace{1em}(8)}$$
类似的一阶近似也适用于对数:
$$\log (\mathrm{Exp}(\mathbf{\varphi })\mathrm{Exp}(\delta \varphi ))\approx \mathbf{\varphi }+{\mathrm{J}}_r^{-1}(\mathbf{\varphi })\delta \mathbf{\varphi }\text{\hspace{1em}(9)}$$
右雅可比矩阵逆的显式表达式在补充材料[29]中给出。 $J_r(\mathbf{\varphi })$ reduces to the identity for $\Vert \mathbf{\varphi }\Vert =0$ 。

指数映射的另一个有用的性质是关于伴随矩阵的：
$$\begin{array}{rl}\mathrm{R}\mathrm{Exp}(\varphi ){\mathrm{R}}^{\top }& =\exp \left(\mathrm{R}{\varphi }^{\wedge }{\mathrm{R}}^{\top }\right)=\mathrm{Exp}(\mathrm{R}\varphi )\\ \iff \mathrm{Exp}(\varphi )\mathrm{R}& =\mathrm{R}\mathrm{Exp}\left({\mathrm{R}}^{\top }\mathbf{\varphi }\right)\end{array}\text{\hspace{1em}(11)}$$

SE(3)

SE(3)描述了三维刚体运动群，定义为 $\text{SE}(3)\equiv \{(\mathbf{R},\mathbf{p}):\mathbf{R}\in \text{SO(3)},\mathbf{p}\in {\mathbb{R}}^3\}$ 。群运算是 ${\mathbf{T}}_1\cdot {\mathbf{T}}_2=({\mathbf{R}}_1{\mathbf{R}}_2,{\mathbf{R}}_1{\mathbf{p}}_2+{\mathbf{R}}_1)$ ，其逆为 ${\mathbf{T}}_1^{-1}=({\mathbf{R}}_1^T,-{\mathbf{R}}_1^T{\mathbf{p}}_1)$ ， SE(3)的指数映射和对数映射在[32]中定义。 但是，本文不需要这些，原因将在第II-C节中说明。

SO(3)中不确定的描述

SO(3)中不确定度的定义：tangent空间中的一个分布，然后通过指数映射(6)将其映射到SO(3) [32-34]:
$$\tilde{\mathrm{R}}=\mathrm{R}\mathrm{Exp}(ϵ),ϵ\sim \mathcal{N}(0,\Sigma )\text{\hspace{1em}(12)}$$
其中 $\mathbf{R}$ 是 一个给定的无噪声旋转(均值), $ϵ$ 为均值为零的小的正态分布扰动。

随机变量 $\tilde{\mathbf{R}}\in \text{SO}(3)$ 的分布可以被显式计算，如[33]一样，得到：
$$p(\tilde{\mathrm{R}})=\beta (\tilde{\mathrm{R}})e^{-\frac{1}{2}{\Vert \text{Log}\left({\mathrm{R}}^{-1}\tilde{\mathrm{R}}\right)\Vert }_{\Sigma }^2}\text{\hspace{1em}(13)}$$
其中 $\beta (\tilde{\mathbf{R}})$ 是归一化因子，近似计算： $\beta (\tilde{\mathbf{R}})\simeq 1/\sqrt{2\pi \text{det}(\Sigma )}$ ，其中 $\Sigma$ 很小。 如果将 $\beta$ 近似为一个常数，那么给定一个测量 $\tilde{\mathbf{R}}$ ，旋转 $\mathbf{R}$ 的负对数似然为：
$$\mathcal{L}(\mathrm{R})=\frac{1}{2}{\Vert \text{Log}\left({\mathrm{R}}^{-1}\tilde{\mathrm{R}}\right)\Vert }_{\Sigma }^2+\text{const}=\frac{1}{2}{\Vert \text{Log}\left({\tilde{\mathrm{R}}}^{-1}\mathrm{R}\right)\Vert }_{\Sigma }^2+\text{const}\text{\hspace{1em}(14)}$$

流形上的高斯牛顿方法

关于流形： 流形优化： Manifold Optimization 的 全网最通俗版本详解 (一）

考虑一个优化问题 ${\min }_{x\in \mathcal{M}}f(x)$ ，其中 $f(\cdot )$ 是给定的代价函数，变量 $x$ 属于流形 $\mathcal{M}$ ; 为了简单起见，考虑一个单一变量，因而描述可以很容易地一般化。

流形优化的一种标准方法[35,36]包括定义一个retraction ${\mathcal{R}}_x$ ，它是tangent空间(在 $x$ 处)的元素 $\delta x$ 与 $x\in \mathcal{M}$ 的邻域之间的一个双射映射。 使用retraction，可以重新参数化问题如下:
$$\underset{x\in \mathcal{M}}{\min }f(x)\Rightarrow \underset{\delta x\in {\mathbb{R}}^n}{\min }f\left({\mathcal{R}}_x(\delta x)\right)$$
重新参数化通常称为提升（lifting）[35]。 粗略地说，我们在当前估计定义的tangent空间中工作，它在局部表现为欧氏空间。 现在可以将标准优化技术应用于(14)中右边的问题。 在GN框架中，将cost围绕当前估计进行平方计算。 然后求解二次逼近得到在正切空间中向量 $\delta x^{\star }$ 。最后，流形上的当前猜测被更新为 $\hat{x}\leftarrow {\mathcal{R}}_{\hat{x}}(\delta x^{\star })$ 。

一个可能的retraction是指数映射。在计算上，这可能不是最方便的，参见[37]。

对于SE(3)，使用下面的retraction， 在 $\mathbf{T}=(\mathbf{R},\mathbf{p})$ ：
$${\mathcal{R}}_{\mathrm{T}}(\delta \mathbf{\varphi },\delta \mathbf{p})=(\mathrm{R}\mathrm{Exp}(\delta \mathbf{\varphi }),\mathbf{p}+\mathrm{R}\delta \mathbf{p}),\left[\begin{array}{ll}\delta \mathbf{\varphi }& \delta \mathbf{p}\end{array}\right]\in {\mathbb{R}}^6\text{\hspace{1em}(15)}$$
这解释了为什么在第II-A节中，只定义了SO(3)的指数映射:有了这种选择就不需要计算SE(3)的指数映射。

视觉惯性状态估计的MAP

系统和假设： 考虑一个VIN问题，在这个问题中想要跟踪一个装有IMU和单目相机的传感系统 (例如，一个移动机器人或手持设备) 的状态。 假设IMU帧“B”与想要跟踪的body帧重合，并且相机和IMU之间的变换（外参）是固定的，且预先标定了（图3）。 假设SLAM前端提供未知位置的3D路标的像素测量。且得到了一个称为关键帧[16]的图像子集，对其计算位姿估计。

状态：系统在 $i$ 时刻的状态用IMU的方向、位置、速度和bias来描述: ${\mathbf{x}}_i\equiv [{\mathbf{R}}_i,{\mathbf{p}}_i,{\mathbf{v}}_i,{\mathbf{b}}_i]$ ，其中 $({\mathbf{R}}_i,{\mathbf{p}}_i)\in \text{SE(3)}$ ，速度在向量空间中即 ${\mathbf{v}}_i\in {\mathbb{R}}^3$ ，IMU bias可以写成 ${\mathbf{b}}_i=[{\mathbf{b}}_i^g,{\mathbf{b}}_i^a]\in {\mathbb{R}}^6$ ，其中 ${\mathbf{b}}_i^g,{\mathbf{b}}_i^a\in {\mathbb{R}}^3$ 是陀螺仪和加速度计的bias。

记 ${\mathcal{K}}_k$ 为到时刻 $k$ 为止的所有关键帧集合。 这里估计所有关键帧的状态:
X k ≐ { x i } i ∈ K k (16) \mathcal{X}_{k} \doteq\left\{\mathbf{x}_{i}\right\}_{i \in \mathcal{K}_{k}} \tag{16} Xk​≐{xi​}i∈Kk​​(16)
这里采用了一种无结构的方法(参见第六节)，因此3D路标不属于待估计变量的一部分。

测量： 系统输入是来自相机和IMU的测量值。 ${\mathcal{C}}_i$ 为在关键帧 $i$ 的相机测量，在 $i$ 时刻相机可以观察到多个路标 $l$ ，因此 ${\mathcal{C}}_i$ 包含多个像素的观测 ${\mathbf{z}}_{il}$ 。 用 ${\mathcal{I}}_{ij}$ 表示在两个连续关键帧 $i$ 和 $j$ 之间获得的IMU测量集合。 通常每个 ${\mathcal{I}}_{ij}$ 包含数百个IMU测量。到时间 $k$ 收集到的测量集合是
Z k ≐ { C i , I i j } ( i , j ) ∈ K k (17) \mathcal{Z}_{k} \doteq\left\{\mathcal{C}_{i}, \mathcal{I}_{i j}\right\}(i, j) \in \mathcal{K}_{k} \tag{17} Zk​≐{Ci​,Iij​}(i,j)∈Kk​(17)

因子图和MAP估计：给定可用测量 ${\mathcal{Z}}_k$ 和先验 $p({\mathcal{X}}_0)$ ，因子图编码了变量 ${\mathcal{X}}_k$ 的后验概率：
$$\begin{gathered} p\left({\mathcal{X}}_k\mid {\mathcal{Z}}_k\right)\propto p\left({\mathcal{X}}_0\right)p\left({\mathcal{Z}}_k\mid {\mathcal{X}}_k\right)=p\left({\mathcal{X}}_0\right)\prod _{(i,j)\in {\mathcal{K}}_k}p\left({\mathcal{C}}_i,{\mathcal{I}}_{ij}\mid {\mathcal{X}}_k\right) \\ =p\left({\mathcal{X}}_0\right)\prod _{(i,j)\in {\mathcal{K}}_k}p\left({\mathcal{I}}_{ij}\mid {\mathbf{x}}_i,{\mathbf{x}}_j\right)\prod _{i\in {\mathcal{K}}_k}\prod _{l\in {\mathcal{C}}_i}p\left({\mathbf{z}}_{il}\mid {\mathbf{x}}_i\right)\text{\hspace{1em}(18)} \end{gathered}$$
因式分解(18)中的项称为因子（factors）。 图4给出了问题的因子图的连通性示意图(无结构视觉因子的连通性将在第VI节中阐明)。

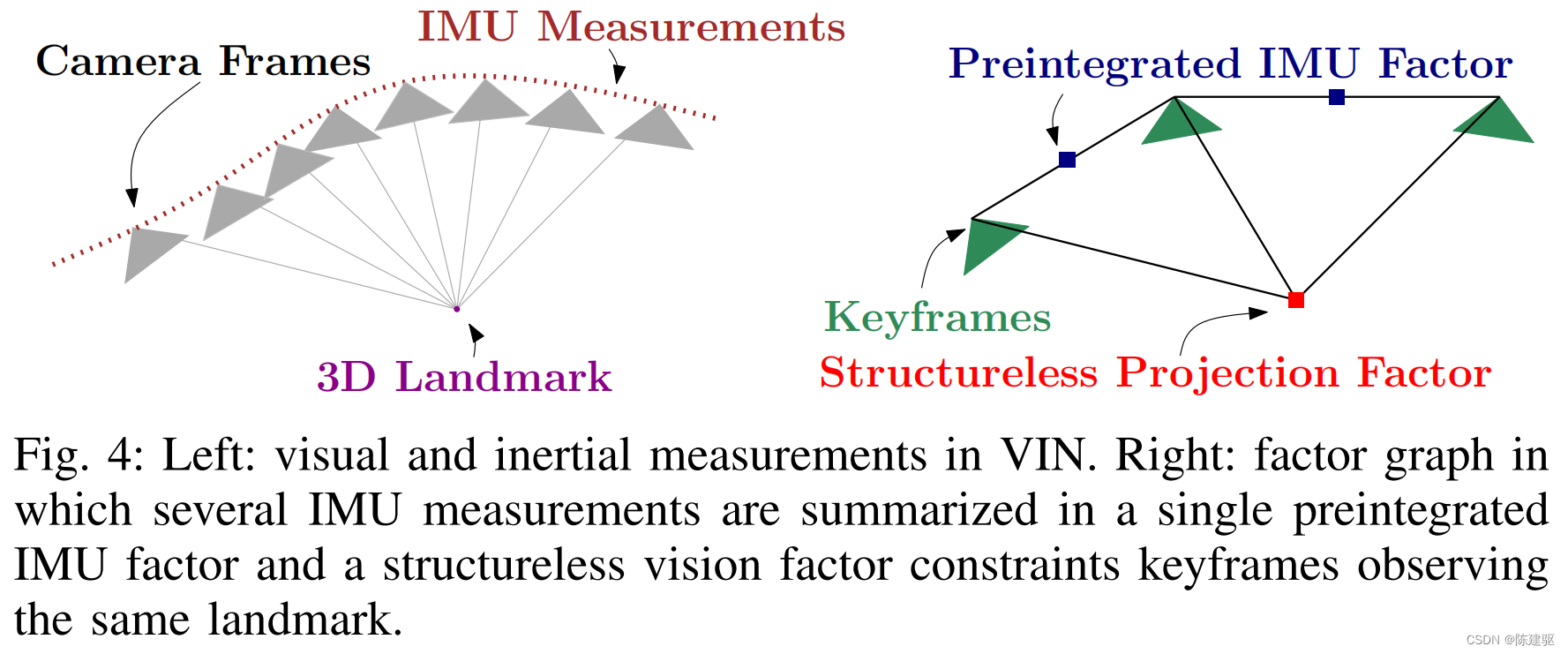
MAP估计对应于公式(18)的最大值，或者等价于负对数后验的最小值。 在零均值高斯噪声的假设下，负对数后验可以写成残差平方和:
$$\begin{gathered} {\mathcal{X}}_k^{\star }\doteq \arg \underset{{\mathcal{X}}_k}{\min }-{\log }_{e}p\left({\mathcal{X}}_k\mid {\mathcal{Z}}_k\right) \\ =\arg \underset{{\mathcal{X}}_k}{\min }{\Vert {\mathbf{r}}_0\Vert }_{{\Sigma }_0}^2+\sum _{(i,j)\in {\mathcal{K}}_k}{\Vert {\mathbf{r}}_{{\mathcal{I}}_{ij}}\Vert }_{{\Sigma }_{ij}}^2+\sum _{i\in {\mathcal{K}}_k}\sum _{l\in {\mathcal{C}}_i}{\Vert {\mathbf{r}}_{{\mathcal{C}}_{il}}\Vert }_{{\Sigma }_{\mathcal{C}}}^2\text{\hspace{1em}(19)} \end{gathered}$$
其中 ${\mathbf{r}}_0$ , ${\mathbf{r}}_{{\mathcal{I}}_{ij}}$ , ${\mathbf{r}}_{{\mathcal{C}}_{il}}$ 是关于测量的残差项， ${\mathbf{\Sigma }}_0$ , ${\mathbf{\Sigma }}_{ij}$ , ${\mathbf{\Sigma }}_{\mathcal{C}}$ 是对应的协方差矩阵。

IMU模型和运动积分

IMU测量相对于惯性系的传感器的转速（rotate rate）和加速度。 测量记为 ${}_B\tilde{\mathbf{a}}(t)$ , ${}_B{\tilde{\mathbf{\omega }}}_{WB}(t)$ ，受到加性白噪声 $\mathbf{\eta }$ 和缓慢变化的传感器bias $\mathbf{b}$ 的影响。
$${}_{\mathrm{B}}{\tilde{\mathbf{\omega }}}_{\mathrm{WB}}(t)={}_{\mathrm{B}}{\mathbf{\omega }}_{\mathrm{WB}}(t)+{\mathbf{b}}^g(t)+{\mathbf{\eta }}^g(t)\text{\hspace{1em}(20)}$$

$${}_{\mathrm{B}}\tilde{\mathbf{a}}(t)={\mathrm{R}}_{\mathrm{wB}}^{\top }(t)\left({}_{\mathrm{w}}\mathbf{a}(t)-{}_{\mathrm{w}}\mathbf{g}\right)+{\mathbf{b}}^a(t)+{\mathbf{\eta }}^a(t)\text{\hspace{1em}(21)}$$

前缀B表示对应的量在坐标系B中表示(c.f.，图3)。 IMU的位姿由变换 ${\mathbf{R}}_{WB}{,}_W\mathbf{p}$ 描述，它将一个点从传感器坐标系B映射到W。向量 ${}_B{\tilde{\mathbf{\omega }}}_{WB}(t)\in {\mathbb{R}}^3$ 为B相对于W的瞬时角速度，在坐标系B中表示； ${}_B\tilde{\mathbf{a}}(t)\in {\mathbb{R}}^3$ 传感器的加速度； ${}_W\mathbf{g}$ 是世界坐标中的重力向量。 这里忽略了地球自转的影响，这相当于假设W是一个惯性系。

现在的目标是从IMU测量中推断系统的运动。为此，引入以下运动学模型[38,39]:
$${\dot{\mathrm{R}}}_{\mathrm{WB}}={\mathrm{R}}_{\mathrm{WB}}{}_{\mathrm{B}}{\mathbf{\omega }}_{\mathrm{WB}}^{\wedge },{}_{\mathrm{w}}\dot{\mathbf{v}}={}_{\mathrm{w}}\mathbf{a},{}_{\mathrm{w}}\dot{\mathbf{p}}={}_{\mathrm{w}}\mathbf{v}\text{\hspace{1em}(22)}$$
这描述了B的姿态和速度的演变。

$t+∆t$ 时刻的状态由式(22)积分得到。 应用欧拉积分，假设 ${}_W\mathbf{a}$ 和 ${}_B{\mathbf{\omega }}_{WB}$ 在区间 $[t,t+∆t]$ 中保持恒定，得到:
$$\begin{array}{rl}{\mathrm{R}}_{\mathrm{WB}}(t+\Delta t)& ={\mathrm{R}}_{\mathrm{WB}}(t)\mathrm{Exp}\left({}_{\mathrm{B}}{\mathbf{\omega }}_{\mathrm{WB}}(t)\Delta t\right)\\ {}_{\mathrm{w}}\mathbf{v}(t+\Delta t)& ={}_{\mathrm{w}}\mathbf{v}(t)+{}_{\mathrm{w}}\mathbf{a}(t)\Delta t\\ {}_{\mathrm{w}}\mathbf{p}(t+\Delta t)& ={}_{\mathrm{w}}\mathbf{p}(t)+{}_{\mathrm{w}}\mathbf{v}(t)\Delta t+\frac{1}{2}{}_{\mathrm{w}}\mathbf{a}(t)\Delta t^2.\end{array}\text{\hspace{1em}(23)}$$
使用公式 (20)-(21)，根据IMU测量可以计算 ${}_W\mathbf{a}$ 和 ${}_B{\mathbf{\omega }}_{WB}$ ，因此(23)为：
$$\begin{array}{rl}\mathrm{R}(t+\Delta t)& =\mathrm{R}(t)\mathrm{Exp}\left(\left(\tilde{\mathbf{\omega }}(t)-{\mathbf{b}}^g(t)-{\mathbf{\eta }}^{gd}(t)\right)\Delta t\right)\\ \mathbf{v}(t+\Delta t)& =\mathbf{v}(t)+\mathbf{g}\Delta t+\mathrm{R}(t)\left(\tilde{\mathbf{a}}(t)-{\mathbf{b}}^a(t)-{\mathbf{\eta }}^{ad}(t)\right)\Delta t\\ \mathbf{p}(t+\Delta t)& =\mathbf{p}(t)+\mathbf{v}(t)\Delta t+\frac{1}{2}\mathbf{g}\Delta t^2\\ & +\frac{1}{2}\mathrm{R}(t)\left(\tilde{\mathbf{a}}(t)-{\mathbf{b}}^a(t)-{\mathbf{\eta }}^{ad}(t)\right)\Delta t^2\end{array}\text{\hspace{1em}(24)}$$
为了可读性去掉了坐标帧的下标。离散时间噪声 ${\mathbf{\eta }}^{gd}$ 的协方差是采样率的函数，与连续时间谱噪声 ${\mathbf{\eta }}^g$ 有关： $\text{Cov}({\mathbf{\eta }}^{gd}(t))=\frac{1}{\Delta t}\text{Cov}({\mathbf{\eta }}^g(t))$ ； ${\mathbf{\eta }}^{ad}$ 也一样，参考附录。

在流形上的IMU预积分

本节包含本文的第一个关键贡献。 虽然Eq.(24)可以很容易地被看作因子图中的概率约束，但它需要在因子图中以较高的速率包含状态。在这里，表明在 $k=i$ 和 $k=j$ 时刻两个关键帧之间的所有测量可以整合为一个单一的复合测量，称为预积分IMU测量，它约束了连续关键帧之间的运动。 这个概念首先在[26]中提出（使用欧拉角），本文通过发展一个适用于流形上预积分的理论来扩展它。

假设IMU与相机同步，并在离散时间 $k$ 提供测量(参见图5) 。

对于 $k=i$ 和 $k=j$ 之间的所有 $∆t$ 区间，迭代IMU积分(24)(c.f，图5)，发现:
$$\begin{gathered} {\mathrm{R}}_j={\mathrm{R}}_i\prod _{k=i}^{j-1}\mathrm{Exp}\left(\left({\tilde{\mathbf{\omega }}}_k-{\mathbf{b}}_k^g-{\mathbf{\eta }}_k^{gd}\right)\Delta t\right) \\ {\mathbf{v}}_j={\mathbf{v}}_i+\mathbf{g}\Delta t_{ij}+\sum _{k=i}^{j-1}{\mathrm{R}}_k\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad}\right)\Delta t \\ {\mathbf{p}}_j={\mathbf{p}}_i+\sum _{k=i}^{j-1}{\mathbf{v}}_k\Delta t+\frac{1}{2}\mathbf{g}\Delta t_{ij}^2+\frac{1}{2}\sum _{k=i}^{j-1}{\mathrm{R}}_k\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad}\right)\Delta t^2\text{\hspace{1em}(25)} \end{gathered}$$
引入缩写： $\Delta t_{ij}\equiv {\sum }_{k=i}^j\Delta t$ ， $(\cdot {)}_i\equiv (\cdot )(t_i)$ 来增强可读性。

虽然Eq.(25)已经提供了时间 $t_i$ 和 $t_j$ 之间运动的估计，但它有一个缺点，即**(25)中的积分必须在时间 $t_i$ 的线性化点发生变化时重新计算**（直观地说，旋转 ${\mathbf{R}}_i$ 的变化意味着所有未来的旋转 ${\mathbf{R}}_k,k=i,\cdots ,j-1$ 的变化，并且有必要重新计算(25)中的求和与乘积）。

本文的目标是避免重复积分。为此定义了以下相对运动增量，它们与 $t_i$ 时刻的位姿和速度无关:
$$\begin{array}{rl}\Delta {\mathrm{R}}_{ij}& \doteq {\mathrm{R}}_i^{\top }{\mathrm{R}}_j=\prod _{k=i}^{j-1}\mathrm{Exp}\left(\left({\tilde{\mathbf{\omega }}}_k-{\mathbf{b}}_k^g-{\mathbf{\eta }}_k^{gd}\right)\Delta t\right)\\ \Delta {\mathbf{v}}_{ij}& \doteq {\mathrm{R}}_i^{\top }\left({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij}\right)=\sum _{k=i}^{j-1}\Delta {\mathrm{R}}_{ik}\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad}\right)\Delta t\\ \Delta {\mathbf{p}}_{ij}& \doteq {\mathrm{R}}_i^{\top }\left({\mathbf{p}}_j-{\mathbf{p}}_i-{\mathbf{v}}_i\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2\right)\\ & =\sum _{k=i}^{j-1}\left[\Delta {\mathbf{v}}_{ik}\Delta t+\frac{1}{2}\Delta {\mathrm{R}}_{ik}\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad}\right)\Delta t^2\right]\\ & =\sum _{k=i}^{j-1}\left[\frac{3}{2}\Delta {\mathrm{R}}_{ik}\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad}\right)\Delta t^2\right]\end{array}\text{\hspace{1em}(26)}$$
其中定义 $\Delta {\mathbf{R}}_{ik}\equiv {\mathbf{R}}_i^T{\mathbf{R}}_k$ ， $\Delta {\mathbf{v}}_{ik}\equiv {\mathbf{v}}_k{\mathbf{v}}_i$ 。

(26)中的求和与乘积仍然是bias的函数。 分两步解决这个问题。在V-A节中，假设 ${\mathbf{b}}_i$ 是已知的; 然后在V-C节中展示了当bias估计发生变化时如何避免重复积分。在本文的其余部分中，假设两个关键帧之间的bias保持不变：
$${\mathbf{b}}_i^g={\mathbf{b}}_{i+1}^g=\dots ={\mathbf{b}}_{j-1}^g,{\mathbf{b}}_i^a={\mathbf{b}}_{i+1}^a=\dots ={\mathbf{b}}_{j-1}^a\text{\hspace{1em}(27)}$$

A.预积分IMU测量

---

Exp函数的线性化：
$$\mathrm{Exp}(\varphi +\delta \varphi )\approx \mathrm{Exp}(\mathbf{\varphi })\mathrm{Exp}\left({\mathrm{J}}_r(\mathbf{\varphi })\delta \mathbf{\varphi }\right)\text{\hspace{1em}(7)}$$
${\mathbf{J}}_r(\mathbf{\varphi })$ 是SO(3)的右雅可比，其将tangent空间中的加性增量与应用于右侧的乘法增量联系起来:
$${\mathrm{J}}_r(\varphi )=\mathbf{I}-\frac{1-\cos (\Vert \varphi \Vert )}{\Vert \varphi {\Vert }^2}{\varphi }^{\wedge }+\frac{\Vert \varphi \Vert -\sin (\Vert \varphi \Vert )}{\Vert {\varphi }^3\Vert }{\left({\varphi }^{\wedge }\right)}^2\text{\hspace{1em}(8)}$$

SO(3)伴随矩阵的性质：
$$\begin{array}{rl}\mathrm{R}\mathrm{Exp}(\varphi ){\mathrm{R}}^{\top }& =\exp \left(\mathrm{R}{\varphi }^{\wedge }{\mathrm{R}}^{\top }\right)=\mathrm{Exp}(\mathrm{R}\varphi )\\ \iff \mathrm{Exp}(\varphi )\mathrm{R}& =\mathrm{R}\mathrm{Exp}\left({\mathrm{R}}^{\top }\mathbf{\varphi }\right)\end{array}\text{\hspace{1em}(11)}$$

---

在本节中假设 $t_i$ 时刻的bias是已知的，现在想要分离(26)中的噪声。 从旋转增量 $∆{\mathbf{R}}_{ij}$ 开始，使用一阶近似公式(7)（旋转噪声是“小”的）并重新排列项，使用式(11)将噪声“移动”到最后:
KaTeX parse error: Expected 'EOF', got '&' at position 71: …\mathrm{R}_{j} &̲=\prod_{k=i}^{j…
公式变形：
$$\begin{array}{rl}\Delta {\mathrm{R}}_{ij}& \stackrel{\text{(eq.7)}}{=}\prod _{k=i}^{j-1}\left[\mathrm{Exp}\left(\left({\tilde{\mathbf{\omega }}}_k-{\mathbf{b}}_i^g\right)\Delta t\right)\mathrm{Exp}\left(-{\mathrm{J}}_r^k{\mathbf{\eta }}_k^{gd}\Delta t\right)\right]\\ & \stackrel{\text{(eq.11)}}{=}\Delta {\tilde{\mathrm{R}}}_{ij}\prod _{k=i}^{j-1}\mathrm{Exp}\left(-\Delta {\tilde{\mathrm{R}}}_{k+1j}^{\top }{\mathrm{J}}_r^k{\mathbf{\eta }}_k^{gd}\Delta t\right)\\ & \doteq \Delta {\tilde{\mathrm{R}}}_{ij}\mathrm{Exp}\left(-\delta {\mathbf{\varphi }}_{ij}\right)\end{array}\text{\hspace{1em}(28)}$$
其中 ${\mathbf{J}}_r^k\equiv {\mathbf{J}}_r^k({\tilde{\mathbf{\omega }}}_k-{\mathbf{b}}_i^g)$ 。定义预积分旋转测量 $\Delta {\tilde{\mathbf{R}}}_{ij}\equiv {\prod }_{k=i}^{j-1}\text{Exp}(({\tilde{\mathbf{\omega }}}_k-{\mathbf{b}}_i^g)\Delta t)$ ， 其噪声 $\delta {\mathbf{\varphi }}_{ij}$ 将在下一节中进一步分析。

---

反对称矩阵的性质：
$${\mathbf{a}}^{\wedge }\mathbf{b}=-{\mathbf{b}}^{\wedge }\mathbf{a},\forall \mathbf{a},\mathbf{b}\in {\mathbb{R}}^3\text{\hspace{1em}(2)}$$
指数映射到一阶近似：
$$\exp \left({\varphi }^{\wedge }\right)\approx \mathbf{I}+{\varphi }^{\wedge }\text{\hspace{1em}(4)}$$

---

将(28)带入到(26)，使用(4)对于 $\text{Exp}(-\delta {\mathbf{\varphi }}_{ij})$ 使用一阶近似，并扔掉高阶的噪声项，可以获得：
$$\begin{gathered} \Delta {\mathbf{v}}_{ij}\doteq {\mathrm{R}}_i^{\top }\left({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij}\right) \\ =\sum _{k=i}^{j-1}\Delta {\mathrm{R}}_{ik}\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad}\right)\Delta t \\ =\sum _{k=i}^{j-1}(\Delta {\mathrm{R}}_{ik}\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a\right)\Delta t-\Delta {\mathrm{R}}_{ik}{\mathbf{\eta }}_k^{ad}\Delta t) \\ \text{代入(28)} \\ =\sum _{k=i}^{j-1}(\Delta {\tilde{\mathrm{R}}}_{ij}\mathrm{Exp}\left(-\delta {\mathbf{\varphi }}_{ij}\right)\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a\right)\Delta t-\Delta {\tilde{\mathrm{R}}}_{ij}\mathrm{Exp}\left(-\delta {\mathbf{\varphi }}_{ij}\right){\mathbf{\eta }}_k^{ad}\Delta t) \end{gathered}$$
变形：
$$\begin{gathered} \Delta {\mathbf{v}}_{ij}\stackrel{\text{ eq.(4) }}{\simeq }\sum _{k=i}^{j-1}\Delta {\tilde{\mathrm{R}}}_{ik}\left(\mathbf{I}-\delta {\mathbf{\varphi }}_{ik}^{\wedge }\right)\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_i^a\right)\Delta t-\Delta {\tilde{\mathrm{R}}}_{ik}{\mathbf{\eta }}_k^{ad}\Delta t \\ \stackrel{\text{ eq.(2) }}{=}\Delta {\tilde{\mathbf{v}}}_{ij}+\sum _{k=i}^{j-1}\left[\Delta {\tilde{\mathrm{R}}}_{ik}{\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_i^a\right)}^{\wedge }\delta {\varphi }_{ik}\Delta t-\Delta {\tilde{\mathrm{R}}}_{ik}{\mathbf{\eta }}_k^{ad}\Delta t\right] \\ \doteq \Delta {\tilde{\mathbf{v}}}_{ij}-\delta {\mathbf{v}}_{ij}\text{\hspace{1em}(29)} \end{gathered}$$
其中定义了预积分速度测量 $\Delta {\tilde{\mathbf{v}}}_{ij}\equiv {\sum }_{k=i}^{j-1}\Delta {\tilde{\mathbf{R}}}_{ik}({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_i^a)\Delta t$ 和它的噪声 $\delta {\mathbf{v}}_{ij}$ 。

同理，将(28)代入(26)中 $\Delta {\mathbf{p}}_{ij}$ 的表达式中，利用一阶近似(4)可得:
$$\begin{gathered} \Delta {\mathbf{p}}_{ij}=\sum _{k=i}^{j-1}\left[\frac{3}{2}\Delta {\mathrm{R}}_{ik}\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad}\right)\Delta t^2\right] \\ \text{代入(28)} \\ \Delta {\mathbf{p}}_{ij}=\sum _{k=i}^{j-1}\left[\frac{3}{2}\Delta {\tilde{\mathrm{R}}}_{ij}\mathrm{Exp}\left(-\delta {\mathbf{\varphi }}_{ij}\right)\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_k^a-{\mathbf{\eta }}_k^{ad}\right)\Delta t^2\right] \end{gathered}$$
变形：
$$\begin{gathered} \Delta {\mathbf{p}}_{ij}\stackrel{\text{ eq.(4)}}{\simeq }\sum _{k=i}^{j-1}\frac{3}{2}\Delta {\tilde{\mathrm{R}}}_{ik}\left(\mathbf{I}-\delta {\mathbf{\varphi }}_{ik}^{\wedge }\right)\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_i^a\right)\Delta t^2-\sum _{k=i}^{j-1}\frac{3}{2}\Delta {\tilde{\mathrm{R}}}_{ik}{\mathbf{\eta }}_k^{ad}\Delta t^2 \\ \stackrel{\text{ eq.(2) }}{=}\Delta {\tilde{\mathbf{p}}}_{ij}+\sum _{k=i}^{j-1}\left[\frac{3}{2}\Delta {\tilde{\mathrm{R}}}_{ik}{\left({\tilde{\mathbf{a}}}_k-{\mathbf{b}}_i^a\right)}^{\wedge }\delta {\mathbf{\varphi }}_{ik}\Delta t^2-\frac{3}{2}\Delta {\tilde{\mathrm{R}}}_{ik}{\mathbf{\eta }}_k^{ad}\Delta t^2\right] \\ \doteq \Delta {\tilde{\mathbf{p}}}_{ij}-\delta {\mathbf{p}}_{ij}\text{\hspace{1em}(30)} \end{gathered}$$
其中定义了预积分位置测量 $\Delta {\tilde{\mathbf{p}}}_{ij}$ 和它的噪声 $\delta {\mathbf{p}}_{ij}$ 。

将(28),(29),(30)代入(26)，最终得到预积分测量模型：
$$\begin{array}{rl}\Delta {\tilde{\mathrm{R}}}_{ij}& ={\mathrm{R}}_i^{\top }{\mathrm{R}}_j\mathrm{Exp}\left(\delta {\varphi }_{ij}\right)\\ \Delta {\tilde{\mathbf{v}}}_{ij}& ={\mathrm{R}}_i^{\top }\left({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij}\right)+\delta {\mathbf{v}}_{ij}\\ \Delta {\tilde{\mathbf{p}}}_{ij}& ={\mathrm{R}}_i^{\top }\left({\mathbf{p}}_j-{\mathbf{p}}_i-{\mathbf{v}}_i\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2\right)+\delta {\mathbf{p}}_{ij}\end{array}\text{\hspace{1em}(31)}$$
其中复合测量被写成(待估计)状态“加上”随机噪声的函数，由随机向量描述 $[\delta {\mathbf{\varphi }}_{ij}^T,\delta {\mathbf{v}}_{ij}^T,\delta {\mathbf{p}}_{ij}^T{]}^T$ 。 下一节将讨论噪声项的性质。