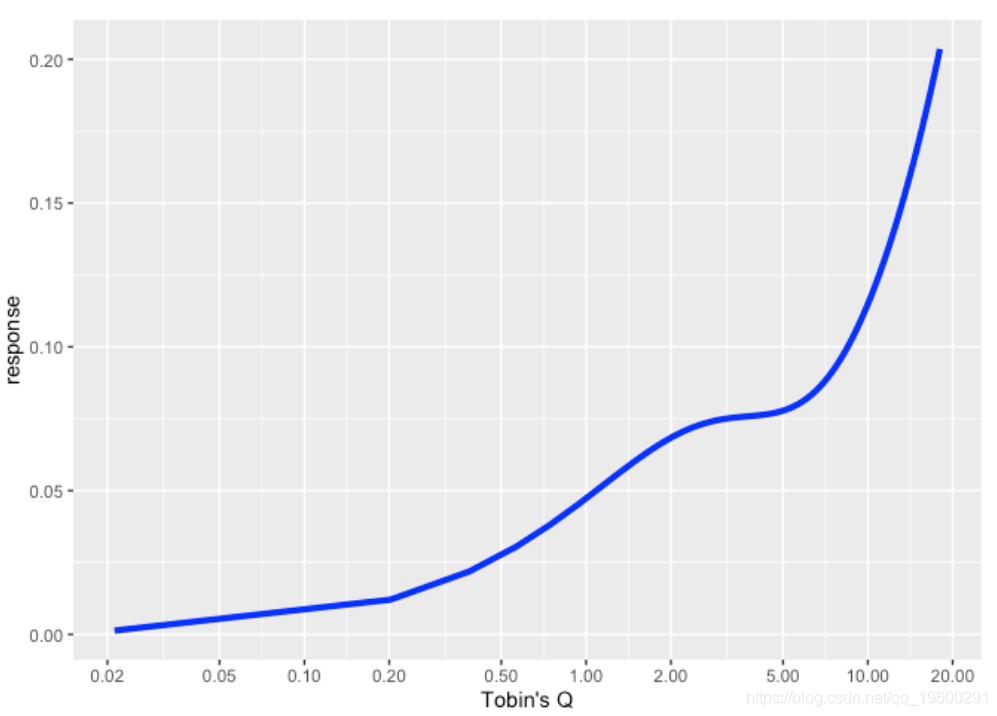
所有子数组的最小值求和。

思路：

最容易想到的就是用DFS找出所有子数组，然后每个子数组找最小值，再求和。但显然不是最优的。
因为费尽心思找到了一堆子数组，它们的最小值竟然是相同的，
是不是有种直接用这个最小值乘以出现的次数就行了，干嘛还要找具体的子数组呢，最小值以外的数字反正又用不上。

现在问题转换为一个最小值会出现在几个子数组中。
比如[3, 1, 2, 4]中的1， 1是子数组的最小值意味着子数组必须包含1，那么含1的子数组有几个呢。
以1为分界线，包含1的左边部分为[3, 1], 右边为[1, 2, 4]
那么含1的子数组个数为两部分长度的乘积2x3 = 6.

因为左边可以是[3,1], [1], 右边可以是[1], [1,2], [1, 2, 4]，即除了1本身，可以选择和不选择其余的数字。
那你说[1,4]也是子数组啊，注意必须是连续的子数组，“连续”二字确实省了不少事。

既然是一片范围的最小值，又面临着怎么选择一段范围的问题。
这片区域必须是最小值，那新的最小值来了怎么办，先把旧的给处理了，把摊子收拾完，再迎接新的摊子。
用stack保存最小值和它的周边，新的最小值来了把stack里面的元素处理掉。

还有一个问题，一直到数组结束也没有新的最小值怎么办，等数组结束了就把stack里面的元素全部处理掉。

如果想追求更快，就用一个数组模拟实现stack，这里就不用了。

    public int sumSubarrayMins(int[] arr) {
        long res = 0;
        int n = arr.length;
        int mod = 1000000007;
        Stack<Integer> st = new Stack<>();
        
        for(int i = 0; i <= n; i++) {
            
            while(!st.isEmpty() && (i == n || arr[i] <= arr[st.peek()])) {
                int j = st.pop();               
                int k = st.isEmpty() ? -1 : st.peek();             
                res += ((long)arr[j] * (j - k) * (i - j)) % mod; //转型为long计算，不然可能会在计算的过程溢出
            }            
            st.push(i);            
        }
        return (int)(res % mod);
    }