目录
3.2.1 安全的基本定义(EAV-安全)
不可区分实验 The adversarial indistinguishability experiment
DEFINITION 3.8 EAV-安全的等价定义(一)
DEFINITION 3.9 EAV-安全的等价定义(二)
证明EAV-安全的两个定义等价
3.2.1 安全的基本定义(EAV-安全)
现代密码学导论-4-完美保密及其三个等价定义_南鸢北折的博客-CSDN博客
EAV-安全和完美不可区分性一样,都是基于不可区分实验而定义的。回顾一下上面链接文章中的不可区分实验。在原实验的基础上做出一些修改:
- 我们现在只考虑在多项式时间内运行的敌手,而定义2.6考虑的甚至是具有无限运行时间的敌手
- 我们现在做出让步,对手确定加密消息的概率可能优于1/2。
- 我们用一个安全参数n来参数化实验。敌手A的运行时间和它的成功概率都被看作是n的函数。正在使用安全参数n运行的实验记作
该实验的输出等于1的概率可以表示为
注意,当A和Π固定时,上述表达式是关于n的函数。
- 我们现在明确地要求对手输出两个长度相等的消息m0,m1。这意味着,在默认情况下,我们不需要一个安全的加密方案来隐藏明文的长度
不可区分实验 The adversarial indistinguishability experiment
- 给定一个输入1^n,敌手A输出一对消息m0,m1,其中|m0| = |m1|。对m0和m1的长度没有限制,只要它们是相同的即可。
- 通过运行Gen(1^n),产生一个输出k;随机选取一个比特b ∈ {0, 1},计算c ← Enck(mb)并返回给敌手A。我们称c为挑战密文
- 敌手A输出一个比特b’
- 如果b ' = b,则定义实验输出为1,否则为0。如果实验的输出为1,我们说敌手A成功了
DEFINITION 3.8 EAV-安全的等价定义(一)
私钥加密方案Π =(Gen,Enc,Dec)如果对于所有PPT敌手,存在一个可忽略函数negl,对于所有的n,
那么我们就说此方案在窃听者存在的情况下具有难以区分的加密,或者是EAV安全的
DEFINITION 3.9 EAV-安全的等价定义(二)
在不可取分实验中,当随机比特b被选定后的实验我们可以表示为:
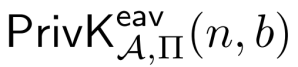
我们将敌手A在上述实验中输出的b’表示为:
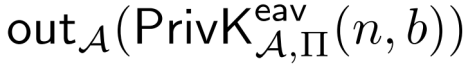
私钥加密方案Π =(Gen,Enc,Dec)如果对于所有PPT敌手,存在一个可忽略函数negl,对于所有的n,
![]() 那么我们就说此方案在窃听者存在的情况下具有难以区分的加密,或者是EAV安全的
那么我们就说此方案在窃听者存在的情况下具有难以区分的加密,或者是EAV安全的
证明EAV-安全的两个定义等价
敌手A成功分为两种情况outA(PrivK(n,0)) = 0和outA(PrivK(n,1)) = 1
我们令P0=Pr[outA(PrivK(n,0)) = 1],P1=Pr[outA(PrivK(n,1)) = 1]
Pr[PrivK(n)=1]=Pr[b=0]*Pr[PrivK(n)=1 | b=0]+Pr[b=1]*Pr[PrivK(n)=1 | b=1]
=0.5*Pr[outA(PrivK(n,0)) = 0]+0.5*Pr[outA(PrivK(n,1)) = 1]
=0.5*(1-P0)+0.5*P1
因此 |Pr[PrivK(n)=1]-1/2|=0.5*|P0-P1|
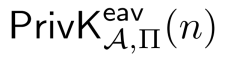
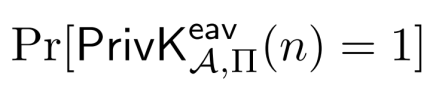
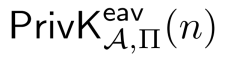
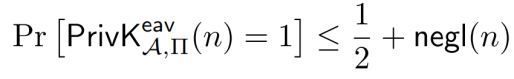
![[b01lers2020]Welcome to Earth](https://img-blog.csdnimg.cn/e985d0b0431142b9a8b41f7b3d326d83.png)


![[激光原理与应用-18]:《激光原理与技术》-4- 粒子数反转与“光”强放大的基本原理](https://img-blog.csdnimg.cn/8b5b6c9acd1045cda23759392cbed36c.png)