提示:唐老师好,我之前因为“阳”了,所以就没有参与汇报,给老师带来不便,请老师见谅。以此篇文章代替课堂汇报。
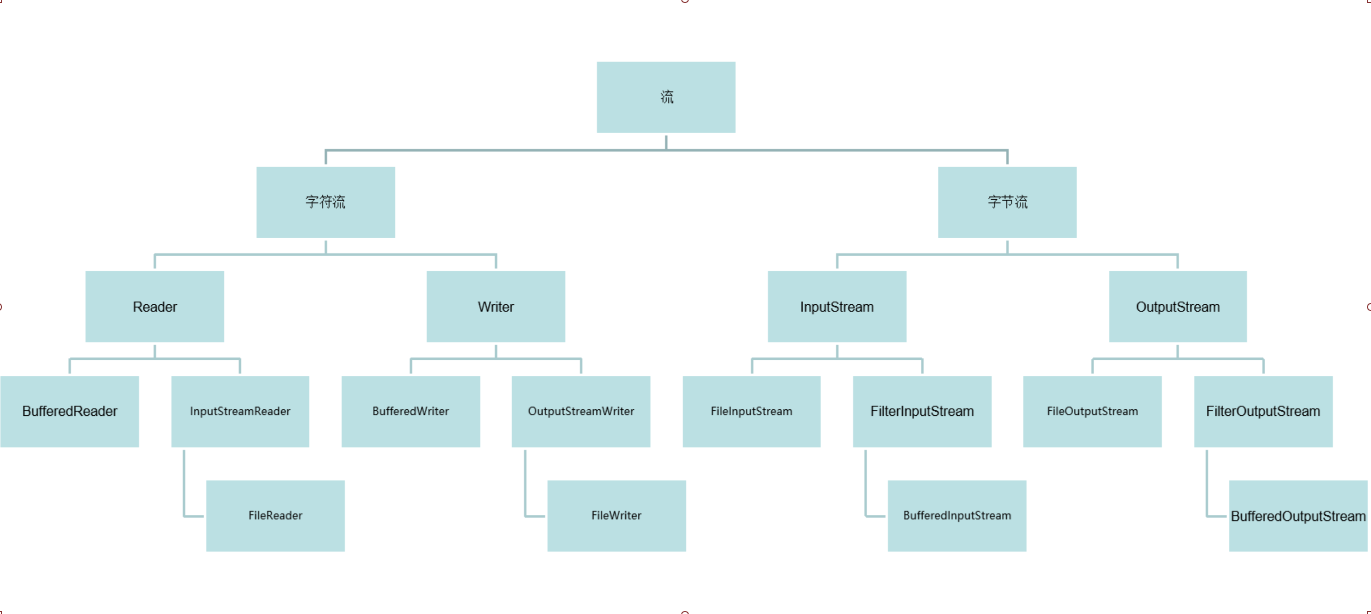
文章目录
- 前言
- 一、不同故障对应的振动频谱和故障特征量
- 二、GIS设备振动特征估计
- 1.GIS设备状态空间
- 2.粒子滤波
- 三、GIS故障检测指标与自适应阈值
- 四、案例分析与仿真
- 总结
- 附录
前言
提示:这里可以添加本文要记录的大概内容:
本文是自己硕士研究生“电气设备智能感知与诊断”课上原本要汇报的内容,但因自己准备期间“阳”了而耽误,故补上一篇博客来代替汇报,写这篇博客一方面是为了代替汇报交作业,另一方面就是单纯想写点东西,加深一下自己对这个问题的理解,也给其他准备处理类似问题的人一点借鉴,本文适合自学,祝你们好运。对根据课堂安排,我们是4个人组成一个小组,每个小组对应一个主题,具体到我所在的小组,主题是GIS组合电气状态监测,分到自己的则是GIS状态检测新技术。当时我准备汇报的新技术是X射线,X射线拍到了照片后,后面研究的重点是各种各样的图像算法,觉得繁杂,且并不能说明某种算法引入以后的意义,就找其他的一些方法(中间看过红外检测等),最后换成基于GIS设备振动特性来判断设备的故障,最主要的文献来自于华电(保定)赵洪山老师团队发表在《高压电器》期刊上的《基于振动特征估计的GIS设备故障检测与分析》,作者是赵洪山老师和高玉峰师兄。这篇文章的主题是基于不同故障时引起的GIS设备振动特征不一样,提出了一种算法,基于这种算法可以判断出发生的故障究竟是放电性故障还是机械性故障,最后作者通过在保定特高压变电站的数据验证这种方法的可行性。这篇文章的重点就在于这个故障检测算法这里(之前还没有抓住这篇文章的重点),如图所示。
 内容是按照以下步骤进行:
内容是按照以下步骤进行:
- 提取GIS外壳振动的数据(有历史上的,也有最新的)的特征量,基于通用自回归建模方法建立GNAP模型。
- 将GNAR模型作为状态转移方程,应用于粒子滤波算法中,构建系统特征估计器。
- 计算振动特征实际测量值与GNAR-PF估计值之间的残差。
- 选择故障检测指标并结合自适应阈值方法检测故障。
提示:以下是本篇文章正文内容,下面案例可供参考
一、不同故障对应的振动频谱和故障特征量
首先,我们要知道GIS设备工作正常时以及工作异常时,金属外壳上的振动频谱是不一样的,有区别的,有差异的,这是我们后面算法分析的大前提。
然后,我们详细分析这两种情况:GIS设备正常工作时,外壳振动基频为100Hz。正常运行时,GIS开关设备振动主要由电磁力与磁致伸缩引起,这两个原因引起的100Hz稳定振动是可以通过理论分析得到的,前者有一个重要的模型就是空心式电流互感器模型,利用这个模型(虽然模型不精确,但一些文献计算外壳功率损耗仍然用这个模型)方便理解GIS设备外壳环流,这个环流在磁场中,设备会受到力的作用,这个力的大小是与电流大小有关,自然就会问环流大小与什么有关,后面自己调研相关文献,知道分三相共箱型和三相分箱型(运行电压等级不一样),具体影响因素也不一样,总体上是三相共箱型外壳环流小,三相分箱型外壳环流大,后面依次列写出三相分箱与三相合箱的电磁力的作用表达式(吐槽一下:CSDN博客插入LaTex公式不是很好用),无论什么哪种情况,在工频情况下,其振动频率自然是100Hz。
三相分箱型:
F
=
B
i
L
(
B
=
μ
0
I
0
sin
(
ω
T
t
)
2
π
R
)
=
μ
0
k
L
I
0
2
sin
2
(
ω
t
)
2
π
R
三相分箱型:F=BiL\left ( B=\frac{\mu _{0}I_{0}\sin \left ( \omega Tt \right ) }{2\pi R} \right ) \\ = \frac{\mu _{0}kLI_{0}^{2} \sin^{2} \left ( \omega t \right ) }{2\pi R}
三相分箱型:F=BiL(B=2πRμ0I0sin(ωTt))=2πRμ0kLI02sin2(ωt)
三相合箱型:
f
=
F
a
l
a
=
B
合
I
a
l
a
l
a
=
3
×
1
0
−
7
×
I
2
d
∣
sin
ω
t
∣
三相合箱型:f=\frac{F_{a} }{l_{a} } =\frac{B_{合} I_{a}l_{a} }{l_{a} } =\frac{\sqrt{3} \times 10^{-7}\times I^{2} }{d}\left | \sin \omega t \right |
三相合箱型:f=laFa=laB合Iala=d3×10−7×I2∣sinωt∣
在后者磁致伸缩引起的振动中,磁畴的理解很关键,本科期间学习电机学时,一开始学习铁磁材料磁滞回线,特别是饱和特性就学到了这个概念,这里在其上的基础拓展了一点,什么是磁致伸缩?通俗理解磁致伸缩就是铁磁材料在磁场下会发生形变,撤掉磁场,形变就消失了(教科书上的定义 磁致伸缩:铁磁性和亚铁磁性物质在外磁场作用下,在磁化方向上会发生伸长或缩短,去掉外加磁场后又恢复其原来的尺寸),理解这种形变。先理解成弹簧模型(见附录我做的PPT),后面深入的话,就会谈到磁畴,可以将其看作成一个个超微型的小磁铁,而且是椭圆形的小磁铁,当外界磁场方向变化时,椭圆形的小磁铁之前由正长轴方向相互连接,后变成反方向相互连接,中间就有个“长-短-长”的变化过程(变化过程见附录我的PPT),工频的话,变化次数就是工频的两倍,这个倍数关系同时也可以由磁学相关公式推导出来(公式见附录PPT)。下面这一页PPT是我原来准备课堂汇报的主体框架,我原本重点是要讲这个正常工作时100Hz是怎么来的,然后提一下异常工作下的振动频率是怎么样的,再简单提一下算法(感觉不好讲,里面由一系列的公式推导,逻辑推断,就打算简单化处理),介绍一下过程,看看仿真结果,就算大致说明了一下这个新方法,后面与唐老师交流,才知道自己是没有抓住核心部分(核心部分是算法部分,不把算法讲清楚,你无法说明这个新方法),对这给新方法是理解是极其肤浅的,根本就没有达到研究生的水准。反思这个过程,这对应自己之前的博客书写是为了更好的思考里面的内容,多渠道与人交流,能加深自己对事物的理解。

异常情况下的外壳震动频率并没有什么明显的特征频率,只有个特征范围。GIS设备常见的缺陷类型统计如下表所示。GIS设备最主要的故障类型就是两种:绝缘型故障和机械型故障。
 机械故障包括紧固螺栓松动、机械卡涩、触头接触不良等,会引起低频振动;绝缘故障主要是由金属突出物、悬浮金属颗粒等局部放电破坏设备内部绝缘引起,振动频率主要在2kHz以上。经过统计,日本学者Okutsu N等学者得到了如下的不同故障类型下GIS设备金属外壳上的振动信号频率、幅值分布情况。 这个图来自于他在上IEEE于1981发表的论文,原论文虽然内容不
机械故障包括紧固螺栓松动、机械卡涩、触头接触不良等,会引起低频振动;绝缘故障主要是由金属突出物、悬浮金属颗粒等局部放电破坏设备内部绝缘引起,振动频率主要在2kHz以上。经过统计,日本学者Okutsu N等学者得到了如下的不同故障类型下GIS设备金属外壳上的振动信号频率、幅值分布情况。 这个图来自于他在上IEEE于1981发表的论文,原论文虽然内容不 多,但这篇文章被引较高,我在知网查阅文献时,几乎有关GIS振动的诊断方法的文章都会提到原文章,或这张图。
多,但这篇文章被引较高,我在知网查阅文献时,几乎有关GIS振动的诊断方法的文章都会提到原文章,或这张图。
从上图我们可以看出机械故障与放电故障的频谱差异,我们选用什么参数来表征这个差异呢?原文作者选用“频段能量比”作为振动特征量(即下面公式中的
x
x
x ),具体将振动频谱图以 2kHz为界,分为“高频段”(同上
E
H
E_{H}
EH )与“低频段”(同上
E
L
E_{L}
EL ),每一个频段累加每一个频率点幅值(同上
A
(
f
)
A(f)
A(f) )的平方,然后这上下两个频段之比取对数。具体如下
x
=
l
g
E
H
E
L
E
H
=
∑
f
=
2001
m
a
x
A
2
(
f
)
E
L
=
∑
f
=
1
2000
A
2
(
f
)
x=lg\frac{E_{H} }{E_{L} } \\E_{H}=\sum_{f=2001}^{max} A^{2}(f) \\E_{L}=\sum_{f=1}^{2000} A^{2}(f)
x=lgELEHEH=f=2001∑maxA2(f)EL=f=1∑2000A2(f)
原文作者选用的分界线是 2kHz,为什么选用这个频率作为分界线呢?2.5kHz行不行?电科院高压所郭碧红老师与张汉华老师的文章《利用GIS外壳典型振动的频率特性检测内部故障潜伏性故障》中给出了自由导电粒子运动和由固定杂质的局部放电时的外壳振动频谱图,如下就是振动放电引起的振动谱图,文章中的图太多了,不一一截图,主要为高频分量。
 徐志钮老师等的文章《机械缺陷对GIS外壳振动影响》中讨论了螺栓松动和导杆不对中这两种缺陷时的振动信号分别与无缺陷正常运行时的差别,里面给出了螺栓松动时和导杆不对中时的振动信号图,如下所示,主要为低频分量
徐志钮老师等的文章《机械缺陷对GIS外壳振动影响》中讨论了螺栓松动和导杆不对中这两种缺陷时的振动信号分别与无缺陷正常运行时的差别,里面给出了螺栓松动时和导杆不对中时的振动信号图,如下所示,主要为低频分量

 从上面的图以及我没有截过来的图可以看出,高频分量与低频分量分界线有多种选择,不一定要用这个2kHz,用这个也行,我们顺着作者的思路就用这个分界线继续分析。
从上面的图以及我没有截过来的图可以看出,高频分量与低频分量分界线有多种选择,不一定要用这个2kHz,用这个也行,我们顺着作者的思路就用这个分界线继续分析。
二、GIS设备振动特征估计
我们已经选择好了振动特征量,现在想一想GIS正常运行(基频是100Hz等,低频分量较小,几乎无高频分量)、机械故障时(低频分量较多,高频分量不多)、放电性故障(低频分量没有高频分量那么多)这三种情况,用频段能量比也差不多可以区别出来,这样故障发生前后,这个振动特征量就发生了变化,即把故障发生后的振动特征量与故障发生前的振动特征量进行比较,具体操作的话,原文作者是基于故障发生前的数据来预测故障发生时的数据,然后用这个估计值来与故障发生时实际测量的数据进行比对,我们前面说了振动特征量在故障发生前后是不一样的,所以这个估计值与实际值是有区别的,一有区别就可以判断出故障, 除了这种方法以外,还有没有别的方法?我还没有弄清楚,此处存疑,后面的结果显示,我们可以隔离放电性故障与及机械性故障。这里涉及两个比较重要的概念:GNAR模型和粒子滤波,下面进行说明。
1.GIS设备状态空间
这里我们使用GNAR模型建立状态空间。先做个解释,GNAR是英文general expression for liner and nonliner auto-regressive time series model(线性和非线性自回归时间序列模型的一般表达式)的缩写,然后这里就谈及了时间序列这一概念i,好像通信的研究生期间有门课程就叫做“现代时间序列”,专门讲这个的,我没有系统学过,只能谈及肤浅的内容。先从时间序列这个概念说起,百度上定义为是指将同一统计指标的数值按其发生的时间先后顺序排列而成的数列,即我们随着时间变化,统计每一个时间点附近的振动特征量,把这些振动统计特征量按照时间的前后顺序排成一个数列就是所谓的时间序列。时间序列分析的主要目的是根据已有的历史数据对未来进行预测。即我们这里振动特征估计值,这里建模的话需要分系统是线性模型还是非线性模型,建模之前需要对系统进行线性检验,不同类型的模型需要用不同的方法,然后原文作者根据陈茹雯老师等的文章《线性/非线性时间序列模型一般表达式及工程应用》,认识到这个GNAR模型的好处在于无须对未知时间序列进行线性/非线性检验(同时使适用于线性与非线性系统),可以直接建模和预测,所以就用这种方法来建模, GIS振动系统明显为非线性系统, 除了这种方法以外,还有没有别的方法?原文没有谈到这种建模方法与其他建模方法的特别指出,此处存疑,表达式如下

式中:
- n j ( j = 1 , 2 , − , p ) n_{j} (j=1,2,-,p) nj(j=1,2,−,p)为各子项的记忆步长; p p p为多项式展开阶数。
- W i 1 , W i 1 , i 2 , − , W i 1 , i 2 , − , i p W_{i1},W_{i1,i2} ,-,W_{i1,i2,-,ip} Wi1,Wi1,i2,−,Wi1,i2,−,ip为子项的模型参数,一般未知,需要求。
- x t x_{t} xt表示系统t时刻特征量(振动特征量)的取值 。
- a t a_{t} at为模型误差,满足正态分布。
将上式写成如下的矩阵表达式。这里我们就要就要求解这个模型参数(即下面中
W
W
W,即由模型参数组成的矩阵),用什么方法求呢,原文作者用最小二乘估计来求的,的确最小二乘法可以解决这个问题,常见于回归分析做参数估计, 这里有没有什么非用不可的道理呢?,此处存疑。做参数估计需要数据,数据哪里来,这里要么来自之前统计的数据,要么就是做实验测得的数据,然后经过一系列公式推导(中间涉及一些变量代换等过程,我又没有数据,无法将变化过程给表示出来,故略过这一步)
x
t
=
G
t
T
W
+
a
t
x_{t} =G_{t}^{T}W+a_{t}
xt=GtTW+at
可以得到状态方程如下:
X
t
+
1
=
E
X
t
+
A
{
t
r
[
(
X
t
X
t
T
)
(
B
X
)
]
}
+
C
[
t
r
(
D
X
t
X
t
T
)
]
+
F
a
t
X_{t+1} =EX_{t} +A\left \{ tr\left [ \left ( X_{t}X_{t}^{T} \right ) \left ( BX \right ) \right ] \right \}+C\left [ tr\left ( DX_{t}X_{t}^{T} \right ) \right ] +Fa_{t}
Xt+1=EXt+A{tr[(XtXtT)(BX)]}+C[tr(DXtXtT)]+Fat
式中:
- X t + 1 = [ x t , x t − 1 , − , x t − p ] X_{t+1} =[x_{t},x_{t-1},-,x_{t-p} ] Xt+1=[xt,xt−1,−,xt−p]为 t t t时刻特征变量, X t = [ x t − 1 , x t − 2 , − , x t − p − 1 ] X_{t} =[x_{t-1},x_{t-2},-,x_{t-p-1} ] Xt=[xt−1,xt−2,−,xt−p−1]为 t − 1 t-1 t−1时刻特征变量。
- A = C = F = [ 1 , 0 , ⋅ ⋅ ⋅ , 0 ] T A=C=F=[1,0,···,0]^{T} A=C=F=[1,0,⋅⋅⋅,0]T为 p × 1 p\times 1 p×1 维向量。
- X X X表示 p × p p\times p p×p维子项都为 X t X_{t} Xt的分块矩阵。
- B B B表示 p × p p\times p p×p分块参数矩阵,各子项 B i j = [ W i , j , 1 , ⋅ ⋅ ⋅ , W i , j , p ] B_{ij} =\left [ W_{i,j,1},···,W_{i,j,p} \right ] Bij=[Wi,j,1,⋅⋅⋅,Wi,j,p]。
- D = [ w 1 , 1 ⋯ w 1 , p 0 0 ⋱ ⋮ 0 0 0 w p , p 0 0 0 0 0 ] D=\begin{bmatrix} w_{1,1} & \cdots & w_{1,p} & 0\\ 0& \ddots & \vdots &0 \\ 0& 0& w_{p,p}& 0\\ 0& 0& 0&0 \end{bmatrix} D= w1,1000⋯⋱00w1,p⋮wp,p00000
- E = [ w 1 w 2 ⋯ w p 1 0 0 0 0 ⋱ 0 0 0 0 1 0 ] E=\begin{bmatrix} w_{1} & w_{2} & \cdots & w_{p}\\ 1& 0 & 0&0 \\ 0& \ddots & 0& 0\\ 0& 0& 1&0 \end{bmatrix} E= w1100w20⋱0⋯001wp000
输出方程如下:
Y
t
+
1
=
H
X
t
+
v
t
Y_{t+1} =HX_{t} +v_{t}
Yt+1=HXt+vt
式中:
- Y t + 1 Y_{t+1} Yt+1为 t + 1 t+1 t+1时刻观测值。
- H = [ 1 0 ⋯ 0 ] T {H=\begin{bmatrix} 1 & 0& \cdots &0 \end{bmatrix}} ^{T} H=[10⋯0]T为 p × 1 p\times 1 p×1维参数向量。
- v t v_{t} vt为系统参数误差。
2.粒子滤波
将从上式知
t
+
1
t+1
t+1时刻观测值,即 大约就是我们振动变量估计值,为什么说是’大约就是‘?这里要介绍几种概念,对于观测方程,需要进一步说明,任何观测方程都涉及3个量的问题,分别是真实值,测量值和滤波值。真实值是绝对存在但永远无法获得的;测量值是我们用传感器等观测工具获得能反映真实值大小的值,这个值与真实值相比是携带误差的;测量值经过滤波器优化之后得到的数值为滤波值。滤波的目的在于降低噪声的干扰,使滤波结果接近真实值,这三个量的关系如下图所示。

粒子滤波在这里的作用就是为了获得更加接近实际的状态估计值,即振动特征量。原文作者这里只大致提到了状态预测、状态更新和重采样这三个过程,都只是列了几道公式来说明这个过程,这对于新手来说,很难看懂,网上不少博客内容也是这样问题,本来就是很复杂的内容,偏偏要用繁琐,高深的语言来讲解,我看了不少文献,没有看懂多少,只找到黄小平老师等的《粒子滤波原理及应用》还算可以,适合自学,这本书封面如下。下面我尽可能用通俗易懂的语言来讲解什么是粒子滤波。

三、GIS故障检测指标与自适应阈值
前面经过结合粒子滤波的通用回归模型的特征估计器,得到的数值就是我们状态估计值,然后这给状态估计值与实际测量值之间差为残差,残差有正有负,估计值不一定刚好估计在真实值上,选择残差作为检测指标有问题,故选择残差的绝对值作为检测指标。考虑到设备振动的波动性,选择固定阈值会有问题比如误报警,故选择自适应阈值,什么是自适应阈值?就是阈值不是固定,而是随着时间在发生变化。以原文中图来说明。

这样就没有问题了
四、案例分析与仿真
原文作者经过保定特高压变电站的数据分析,先进行故障检测,有机械故障的检测结果图

放电性故障的结果图

后面进行故障隔离检测,结果图如下

仿真结果证明了这种算法的可行。
因为赵洪山老师是保定校区的老师,我其实是和赵老师发过电子邮件,我向赵老师提了一些问题,比如数据能不能发给我,机械性故障时所有常见的缺陷吗?比如螺栓松动,导杆不对中,放电性故障也是如此等,但赵老师至今没有回我,下面是邮件截图
总结
今天是2023年1月21日,除夕之夜
愿天上人间,占得欢娱,年年今夜 -宋·柳永《二郎神·炎光谢》
祝大家福启新岁,万事顺遂