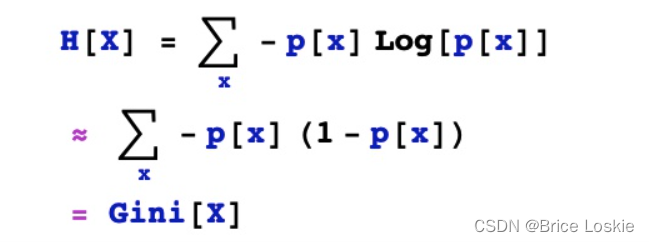1. 请使用泰勒展开推导gini不纯度公式；

2. 请说明树的剪枝怎么实现；

●预剪枝（pre-pruning）通过替换决策树生成算法中的停止准则。（例如，最大树深度或信息增益大于某一阈值）来实现树的简化。预剪枝方法被认为是更高效的方法，因为它们不会反映整个数据集，而是从一开始就保持小树。预剪枝方法有一个共同的问题，即视界限制效应。一般不希望通过停止准则过早地终止诱导。

●后剪枝（post-pruning）是简化树的常见方法，用叶子代替中间节点和子树以提高复杂度。后剪枝不仅可以显著减小树的大小，还可以提高未见过的样本数据的分类精度。可能会出现在测试集上的预测准确率变差的问题，但树的分类准确率总体上会提高。

经典的剪枝算法如表

代价复杂度剪枝方法在1984年Breiman的经典CART算法中首次提到并使用，是一种后剪枝方法。

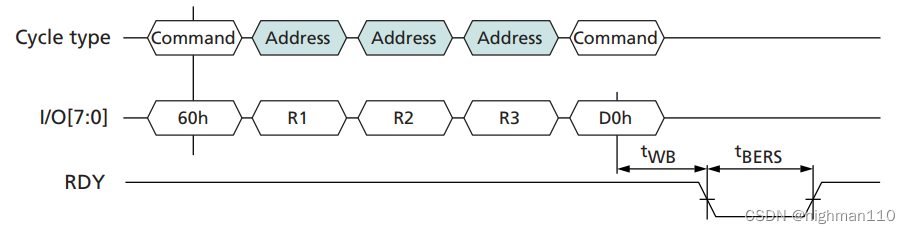
假设对于一棵CART决策树，R(T)是决策树误差（代价），f（T）是一个返回树T的叶子集合的函数。α是一个正则化参数，表示两者的平衡系数，其值越大，树越小，反之树越大。

一棵树的好坏用下式衡量：

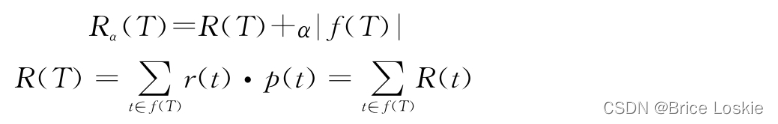
其中 $\sum_{t \in f(T)} R(t)$ 表示每个节点所产生的错误分类的误差纸盒。 $p(t)=\frac{n(t)}{n}$ ,n(t)表示叶子节点t所处理的样本记录值，n表示总的样本记录数。r(t)= $r(t)=1-maxx_kp(C_k-t)$ 表示误分类比例。

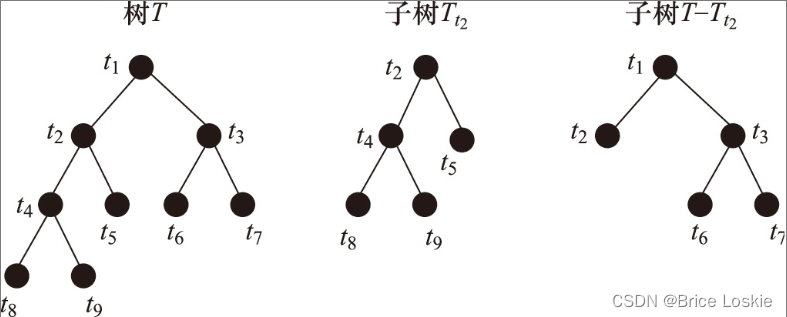
对一颗子树进行剪枝的过程如图。对于待剪枝的决策树T,将一棵以节点t为根节点的子树Tt替换为一个叶子节点，得到子树 $T-T_t$ ,那么, $R_\alpha(T-T_t)-R_a(T)$ 就是剪枝降低决策树复杂度的同事带来的代价变化。

CCP算法的完整流程如下。

1.初始化

假设α′=0，CART算法构建的原始决策树为T1且已经使R（T）最小化。

2. 步骤1

从决策树 $T^1$ 选择分支节点t∈ $T^1$ ，将以分支节点t为根节点的子树替换为叶子节点之后的决策树记为 $T^1_t$ ，通过评估子树R（t）和决策树R（ $T^1_t$ ）的误差，选择使下式最小化的分支节点t：

假设选出的分支节点为 $t_1$ ,那么, $\alpha ^2=max\{\alpha^1,g_1(t_1)\}$ ,新得到的决策树为 $T^2=T^1-T^1_{t1}$

3. 步骤2

决策树 $T^i$ 选择分支节点t∈ $T^i$ ，将以分支节点t为根节点的子树替换为叶子节点之后的决策树记为 $T^i_t$ ，最小化下式：

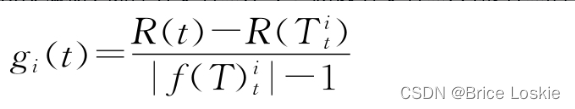
假设选出的分支节点为 $t_i$ ,那么 $\alpha_{i+1}=max\{\alpha_i,g_i(t_i)\}$ ,新得到的决策树为 $T^{i+1}=T^i-T^i_{ti}$

4. 输出

这样，每一个步骤都会生成一个剪枝后的决策树和对应的α值。即

●一系列的决策树Ti，且有 $T^1T^2...T^k$ …{root}。

●一系列的αi值，且有 $\alpha^1\leq \alpha^2 \leq ... \leq \alpha^k...$ 。如何选择合适的α值，从这一系列的决策树中选择出最后剪枝后的决策树呢？可以使用交叉验证，实现最小化的验证误差，这有助于避免过拟合。

下面我们举一个例子，看看CCP算法的具体演算过程。假设原始决策树如图3.2所示。左边的原始决策树记为 $T^1$ ，分支节点有 $t_1,t_2,t_3$ 。右边是每个数据点的坐标位置，有两种类型的数据点，分别为菱形和三角形。

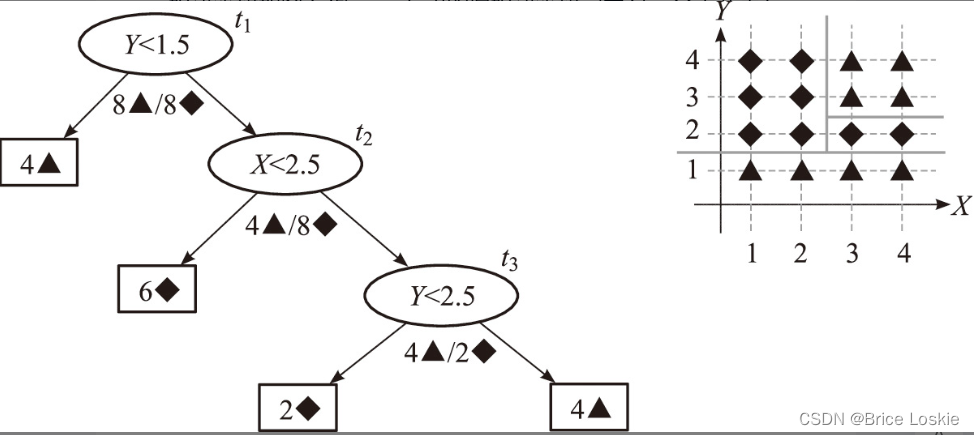
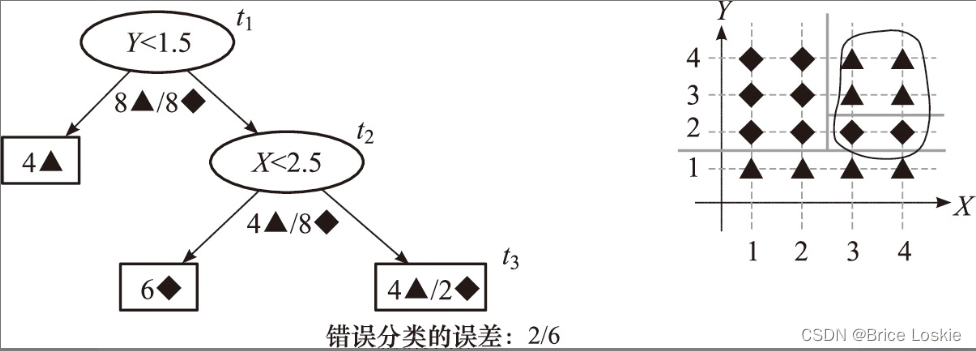
取得最小的g（t）时，t=t2或t=t3，我们选择剪枝最少的情况，因此，将t3为根节点的子树剪除，得到 $\alpha^2=g(t_3)=1/8$ 。剪枝后的决策树 $T^2$ 如图

接下来进行第2次迭代，对于决策树 $T^2$ ，只有两个分支节点 $t_1$ 和 $t_2$ ，同理计算得到表

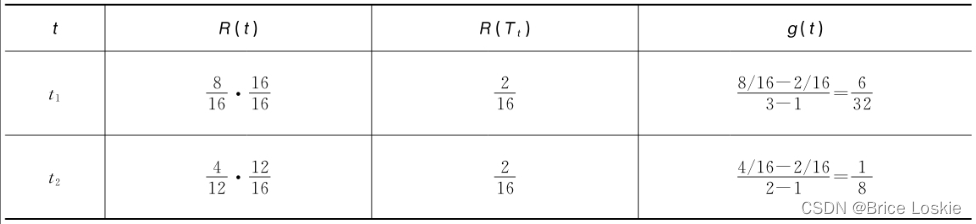
g（t2）=1/8为最小，因此将以t2为根节点的子树剪除，得到α3=g（t2）=1/8。剪枝后的决策树T3如图

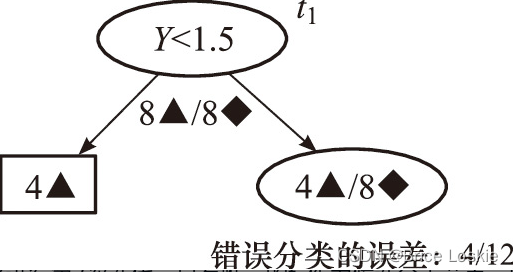
接下来进行第3次迭代，只有唯一的t1作为候选分支节点，因此剪枝得到决策树 $T^4$ ，且

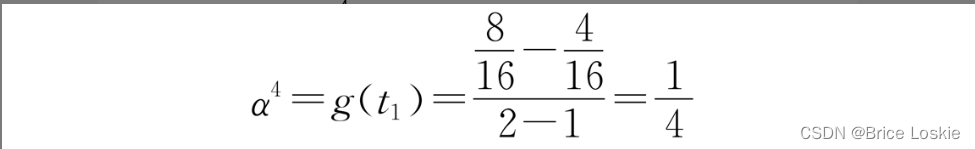
这样，我们就有了一系列的决策树T1、T2、T3、T4以及对应的 $\alpha 1=0,\alpha 2=1/8,\alpha 3=1/8,\alpha 4=1/4$ ，因此，根据选择的α值，可以得到代价复杂度最小化的决策树，如果0＜α≤1/8，则可以选择T2或T3，如果1/8＜α≤1/4，则选择T4。或者通过交叉验证，选择合适的决策树。

3. 请说明回归树怎么实现回归；

3.1 回归决策树的特征和分割点选择准则

CART分类树采用基尼指数最小化准则或基尼增益最大化原则，而CART回归树常用均方误差（Mean Squared Error，MSE或L2）最小化准则作为特征和分割点的选择方法。

事实上，对于回归树来说，常见的三种不纯度测量方法是［假设预测的均值为 $\bar{y}_m$ ]

●均方误差最小化方法，即最小二乘法。这种方法类似于线性模型中的最小二乘法。分割的选择是为了最小化每个节点中观测值和平均值之间的误差平方和。该方法将节点的预测值设置为 $y_m$ 。

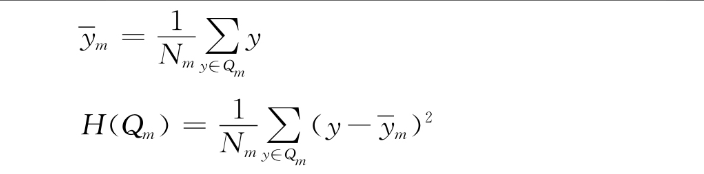
●最小平均绝对误差（Mean Absolute Error，MAE或L1）。这种方法最小化一个节点内平均数与中位数的绝对偏差。与最小二乘法相比，它的优点是对离群值不那么敏感，并提供一个更稳健的模型。缺点是在处理包含大量零值的数据集时不敏感。

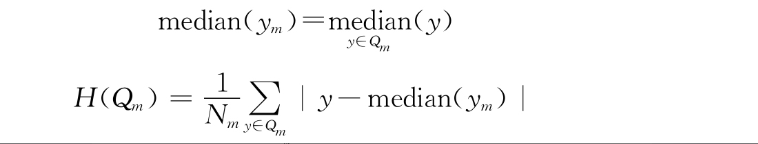
●最小半泊松偏差（half Poisson deviance）

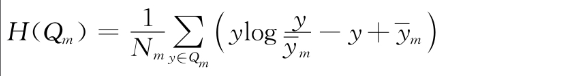
3.2 回归决策树的原理

CART回归树和CART分类树最大的区别在于输出：如果输出的是离散值，则它是一棵分类树；如果输出的是连续值，则它是一棵回归树。

对于回归树，每一个节点都可以被认为是一个回归值，只不过这个值不是最优回归值，只有最底层的节点回归值可能才是理想的回归值。一个节点有回归值，也有分割选择的属性。这样给定一组特征，就知道最终怎么去回归以及回归得到的值是多少了。直觉上，回归树构建过程中，分割是为了最小化每个节点中样本实际观测值和平均值之间的残差平方和。

给定一个数据集 $D=\{(x_1,y_1),(x_2,y_2),...,(x_i,y_i),...,(x_n,y_n)\}$ ,其中 $x_i$ 是m维向量，即 $x_i$ 含有k个特征，记为变量X,是自变量，每个特征记为 $x_j(j=1,2,...,k)$ ,y是因变量。回归问题的目标就是构造一个函数f(X)以拟合数据集D中的样本，是的该函数预测值与样本因变量实际值的均方误差最小。即

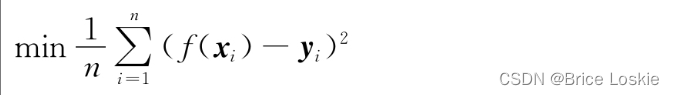
用CART进行回归，目标也是一样的，即最小化均方误差。假设一棵构建好的CART回归树有M个叶子节点，这意味着CART将m维输入空间X划分成了M个单元 $R1,R2,...,R_M$ ,同时意味着CART至多会有M个不同的预测值。CART最小化均方误差公式如下：

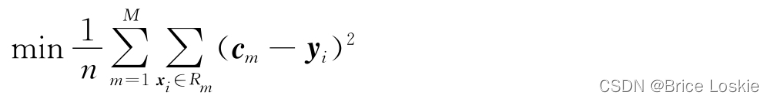
其中， $c_m$ 表示第m个叶子节点的预测值。

想要最小化CART回归树总体的均方误差，只需要最小化每一个叶子节点的均方误差即可，而最小化一个叶子节点的均方误差，只需要将预测值设定为叶子中含有的训练集元素的均值，即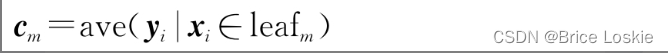

所以，在每一次分割时，需要选择分割特征变量（splitting variable）和分割点（splitting point），使得模型在训练集上的均方误差最小。

这里采用启发式的方法，遍历所有的分割特征变量和分割点，然后选出叶子节点均方误差之和最小的那种情况作为划分。选择第j个特征变量 $x_j$ 和它的取值s，作为分割变量和分割点，则分割变量和分割点将父节点的输入空间一分为二：

CART选择分割特征变量 $x_j$ 和分割点s的公式如下：

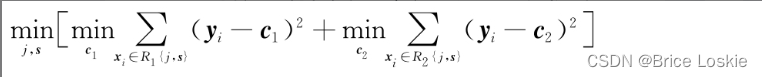
采取遍历的方式，我们可以求出j和s。先任意选择一个特征变量 $x_j$ ，再选出在该特征下的最佳划分s；对每一个特征变量都这样做，得到k个特征的最佳分割点，从这k个值中取最小值即可得到令全局最优的 $(j,s)$ .根据这个（j，s）就可以构建一个节点，然后形成两个子区间。之后分别对这两个子区间继续上述过程，就可以继续创建回归树的节点，直到满足结束条件才停止对区间的划分。

最小二乘回归树生成算法的主要思路为在训练数据集所在的输入空间中，递归地将每个区域划分为两个子区域并决定两个子区域上的输出值，构建二叉决策树。其输入为训练数据集D，输出为回归树 $f(x)$ 。具体的算法流程如下：

1）选择最优切分变量j与切分点s，求解式(2.34).遍历变量j,对固定的切分变量j扫描切分点s，选择使式分割公式使得达到最小值的对(j,s)。

2）用选定的对(j,s)划分区域并决定相应的输出值。

3）继续对两个子区域调用步骤1和2直至满足停止条件。

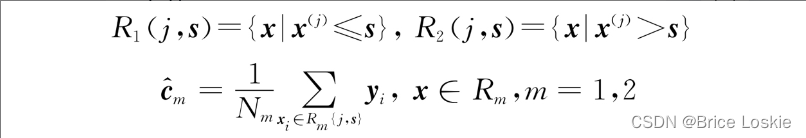
4）将输入空间划分为M个区域R1，R2，…，RM，生成决策树：

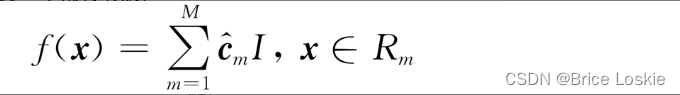
3.3 回归树代码实战

from cart import CartRegressor
from tree_plotter import tree_plot
from sklearn.metrics import r2_score
import numpy as np
import csv


"""加载数据集
"""
# 加载“流行歌手喜好度”数据集
with open("data/popular_singer_preference.csv", "r", encoding="gbk") as f:
    text = list(csv.reader(f))
    for i in range(len(text))[1:]:
        if text[i][1]=='male':
            text[i][1] = 1
        else:
            text[i][1] = 0
    feature_names = np.array(text[0][:-1])
    y_name = text[0][-1]
    X = np.array([v[:-1] for v in text[1:]]).astype('float')
    y = np.array([v[-1] for v in text[1:]]).astype('float')
    X_train, X_test, y_train, y_test = X, X, y, y

"""创建决策树对象
"""
dt = CartRegressor(use_gpu=False, bit=3, min_samples_split=5)

"""训练
"""
model = dt.train(X_train, y_train, feature_names)
print("model=", model)

"""预测
"""
y_pred = dt.predict(X_test)
print("y_real=", y_test)
print("y_pred=", y_pred)
print("test dataset r2={}".format(r2_score(y_test, y_pred)))

"""绘制
"""
tree_plot(model)

"""结束
"""
print("Finished.")