数据结构与算法的学习笔记目录:《恋上数据结构与算法》的学习笔记 目录索引
算法概述
- 1. 算法和数据结构
- 1.1 什么是算法
- 1.2 什么是数据结构
- 2. 时间复杂度
- 2.1 如何判断一个算法的好坏呢?
- 2.2 基本操作执行次数
- 2.3 大O表示法
- 3. 空间复杂度
- 3.1 概念定义
- 4. 算法优化
- 5. 总结
1. 算法和数据结构
1.1 什么是算法
算法是用于解决特定问题的一系列的执行步骤(方法)。
比如:计算a和b的之和、计算1+2+3+…+n的和
//计算a和b的之和
public static int plus(int a, int b){
return a + b;
}
//计算1+2+3...+n的和
public static int sum(int n){
int result = 0;
for(int i = 1; i <= n; i++){
result += i;
}
return result;
}
求解以上示例的方式不局限于上面所说,还可以采用其他方法进行编码,不管采用何种方式,它们之间效率是又区别的。因此,使用不同的算法,解决同一个问题,效率可能相差非常大。比如:求第n个斐波那契数(fibonacci number)。
1.2 什么是数据结构
算法的概念大家大致明白了吧,那数据结构又是什么呢?
我的理解是:数据结构是算法的基石。如果把算法比喻成美丽灵动的舞者,那么数据结构就是舞者脚下广阔而坚定的舞台。
数据结构(data structure),是数据的组织、管理和存储格式,其使用目的是为了高效地 访问 和 修改数据。
那你们知道数据结构都有哪些组成方式吗?
- 线性结构
线性结构是最简单的数据结构,包括数组、链表、以及由它们衍生出来的栈、队列、哈希表… - 树
舒适相对复杂的数据结构,其中比较又代表性的是二叉树,由它衍生出了二叉堆之类的数据结构… - 图
图是更为复杂的数据结构,因为在图中会呈现出多对多的关联关系… - 其他数据结构
除了以上所说的,还有像跳表、哈希链表、位图等等,之后都会涉及讲解到的。
有了数据结构这个舞台,算法才可以尽情舞蹈。在解决问题时,不同的算法会选用不同的数据结构。例如排序算法中的堆排序,利用的就是二叉堆这样的一种数据结构;再如缓存淘汰算法LRU(Least Recently Used)利用的就是特殊的数据结构哈希链表。
关于算法在不同数据结构上的操作过程,在后续会进行一一的学习滴。
2. 时间复杂度
2.1 如何判断一个算法的好坏呢?
衡量算法的好坏有很多标准,其中最重要的两大标准是算法的时间复杂度和空间复杂度。
那时间复杂度和空间复杂度究竟是什么呢?
某一天,小灰和小黄同时加入同一家公司,老板给他们布置了一个需求,直接用代码实现即可。一天后,小灰和小黄交付了各自的代码,两个的代码实现的功能差不多。但小黄的代码运行一次要花100ms,占用内存5MB;而小灰的代码运行一次要花100s,占用内存500MB。于是…
在上述场景中,小灰虽然也按照老板的要求实现了功能,但他的代码中存在两个很严重的问题。
-
运行时间长
运行别人的代码只要100ms,而运行小灰的代码则要100s,使用者肯定是无法忍受的。 -
占用空间大
别人的代码只消耗5MB的内存,而小灰的代码却要消耗500MB的内存,则会给使用者造成很多麻烦。
由此可见,运行时间的长短和占用内存空间的大小,是衡量一个程序好坏的重要因素。
● 时间复杂度(time complexity):估算程序指令的执行次数(执行时间)
● 空间复杂度(space complexity):估算所需占用的存储空间
但问题来了,如果代码都还没运行,我怎么能预知代码运行所花的时间呢?
由于受影响环境的和输入规模的影响,代码的绝对执行时间是无法预估的。但我们却可以预估代码的基本操作执行次数。
2.2 基本操作执行次数
关于代码的基本操作执行次数,就是说每条语句在操作中执行多少次。下面就举代码例子说明
代码1:T(n) = 1,执行次数是常量
public static void test1(int n) {
// if语句执行次数:1
if (n > 10) {
System.out.println("n > 10");
} else if (n > 5) { // 2
System.out.println("n > 5");
} else {
System.out.println("n <= 5");
}
// for语句执行次数:1(int i = 0) + 4(i < 4) + 4(i ++) + 4(System...) = 13
for (int i = 0; i < 4; i++) {
System.out.println("test");
}
}
代码2:T(n) = 1 + 3n,执行次数是线性的
public static void test2(int n) {
// 1(int i = 0) + 3n(i < n, i++, System...)
for (int i = 0; i < n; i++) {
System.out.println("test");
}
}
代码3:T(n) = 3n^2 + 3n + 1,执行次数是用多项式计算的
public static void test3(int n) {
// 1 + 2n + n * (1 + 3n)【内存循环在外层循环n次基础上在计算次数】
// = 1 + 2n + n + 3n^2
// = 3n^2 + 3n + 1
// O(n^2)
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println("test");
}
}
}
代码4:T(n) = 48n + 1,执行次数是线性的
public static void test4(int n) {
// 1 + 2n + n * (1 + 15 + 15 + 15)
// = 1 + 2n + 46n
// = 48n + 1
for (int i = 0; i < n; i++) {
for (int j = 0; j < 15; j++) {
System.out.println("test");
}
}
}
代码5:T(n) = log2(n),执行次数是对数
public static void test5(int n) {
// 8 = 2^3
// 16 = 2^4
// 3 = log2(8)
// 4 = log2(16)
//log2(n)
while ((n = n / 2) > 0) {
System.out.println("test");
}
}

代码6:T(n) = log5(n),执行次数是对数
public static void test6(int n) {
//25 = 5^2
// log5(n)
while ((n = n / 5) > 0) {
System.out.println("test");
}
}
代码7:T(n) = 1 + 3*log2(n) + 2 * nlog2(n),执行次数是对数
public static void test7(int n) {
// 1 + 2*log2(n) + log2(n) * (1 + 3n)
// = 1 + 3*log2(n) + 2 * nlog2(n)
for (int i = 1; i < n; i = i * 2) {
// 1 + 3n
for (int j = 0; j < n; j++) {
System.out.println("test");
}
}
}

代码8:T(n) = 1 + 3n,执行次数是线性的
public static void test8(int n) {
int a = 10;
int b = 20;
int c = a + b;
int[] array = new int[n];
// 1 + n + n + n
// =
for (int i = 0; i < array.length; i++) {
System.out.println(array[i] + c);
}
}
2.3 大O表示法
有了基本操作执行次数的函数T(n),是否就可以分析和比较代码的运行时间了呢?还是有一定困难的。
例如算法A的执行次数是T(n)=100,算法B的执行次数是T(n)=5n^2,这两个到底谁的运行时间更长一些呢?这就要看n的取值了。
因此,为了解决时间分析的难题,有了渐进时间复杂度( asymptotic time complexity)的概念,其官方定义如下:
若存在函数f(n),使得当n趋近于无穷大时,T(n)/f(n) 的极限值为不等于零的常数,则称f(n) 是 T(n)的同数量级函数。记作 T(n) = O(f(n)),O为算法的渐进时间复杂度,简称为时间复杂度。
因此,渐进时间复杂度用大写O表示,所以也被称为大O表示法。
这个定义好晦涩呀,看不明白!
直白来说,时间复杂度就是把程序的相对执行时间函数T(n)简化为一个数量级,这个数量级可以是n、n2、n3等。
如何推导出时间复杂度呢?有如下几个原则:
● 如果运行时间是常数量级,则用常数1表示
● 只保留时间函数中的最高阶项
● 如果最高阶项存在,则省去最高阶项前面的系数
让我们回头看看刚才那些代码。
代码1:
T(n) = 1,只有常数量级,则转化的时间复杂度为:T(n) = O(1)
代码2:
T(n) = 1 + 3n,最高阶项为3n,省去系数3和常量1,则转化的时间复杂度为:T(n) = O(n)
代码3:
T(n) = 3n^2 + 3n + 1,最高阶项为3n^2,省去系数3、3n和常量1,则转化的时间复杂度为:T(n) = O(n^2)
代码3:
T(n) = 1 + 3*log2(n) + 2 * nlog2(n),最高阶项为 2 * nlog2(n),省去系数2和常量1,则转化的时间复杂度为:
T(n) = O(nlog(n))
注意细节:
1. 大O表示法仅仅是一种粗略的分析模型,是一种估算,能帮助我们短时间内了解一个算法的执行效率
2. 对数阶的细节
a. 对数阶一般省略底数
log2n = log29 ∗ log9n
b. 所以 log2n 、log9n 统称为 logn
常见种类
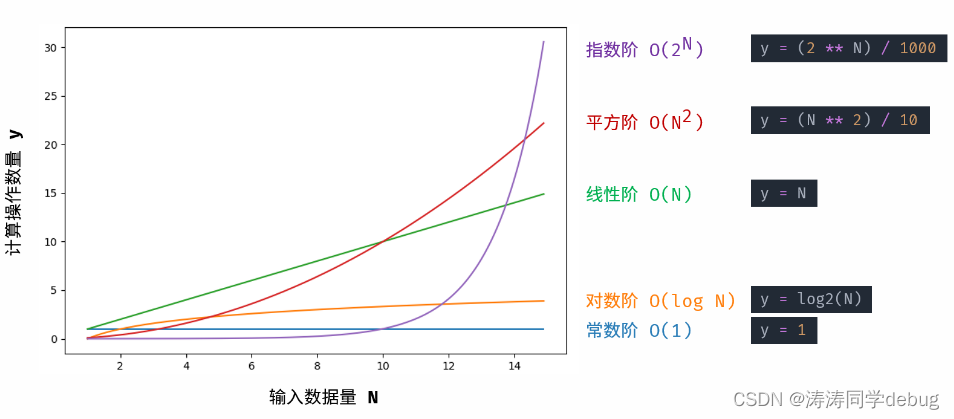
根据从小到大排列,常见的算法时间复杂度主要有:
O(1) < O(log N) < O(N) < O(Nlog N) < O(N^2) < O(2^N) < O(N!) < O(N^N)
3. 空间复杂度
3.1 概念定义
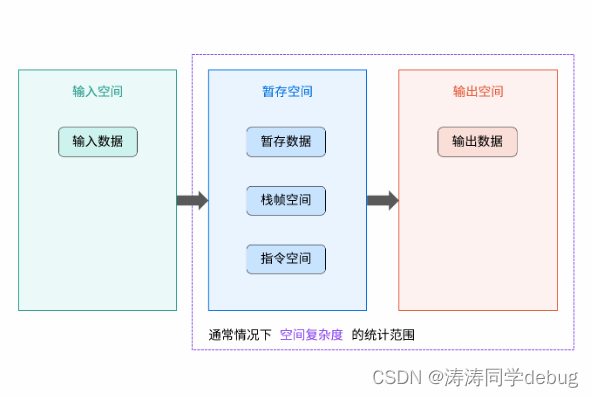
空间复杂度涉及的空间类型有:
● 输入空间: 存储输入数据所需的空间大小;
● 暂存空间: 算法运行过程中,存储所有中间变量和对象等数据所需的空间大小;
● 输出空间: 算法运行返回时,存储输出数据所需的空间大小;
通常情况下,空间复杂度指在输入数据大小为 N 时,算法运行所使用的「暂存空间」+「输出空间」的总体大小。
而根据不同来源,算法使用的内存空间分为三类:
● 指令空间:
编译后,程序指令所使用的内存空间。
● 数据空间:
算法中的各项变量使用的空间,包括:声明的常量、变量、动态数组、动态对象等使用的内存空间。
class Node {
int val;
Node next;
Node(int x) { val = x; }
}
void algorithm(int N) {
int num = N; // 变量
int[] nums = new int[N]; // 动态数组
Node node = new Node(N); // 动态对象
}
● 栈帧空间:
程序调用函数是基于栈实现的,函数在调用期间,占用常量大小的栈帧空间,直至返回后释放。如以下代码所示,在循环中调用函数,每轮调用 test() 返回后,栈帧空间已被释放,因此空间复杂度仍为 O(1)
int test() {
return 0;
}
void algorithm(int N) {
for (int i = 0; i < N; i++) {
test();
}
}
算法中,栈帧空间的累计常出现于递归调用。如以下代码所示,通过递归调用,会同时存在 NN 个未返回的函数 algorithm() ,此时累计使用 O(N)大小的栈帧空间。
int algorithm(int N) {
if (N <= 1) return 1;
return algorithm(N - 1) + 1;
}
4. 算法优化
● 用尽量少的存储空间
● 用尽量少的执行步骤(执行时间)
根据情况,可以
● 空间换时间
● 时间换空间
关于空间复杂度的知识,我们就介绍到这里。时间复杂度和空间复杂度都是学好算法的重要前提,一定要牢牢掌握哦!
5. 总结
- 什么是算法?
- 在计算机领域里,算法是一系列程序指令,用于处理特定的运算和逻辑问题。
- 衡量算法优劣的主要标准是时间复杂度和空间复杂度。
- 什么是数据结构
- 数据结构是数据的组织、管理和存储格式,其使用目的是为了高效地访问和修改数据。
- 数据结构包含数组、链表这样的线性数据结构,也包含树、图这样的复杂数据结构。
- 什么是时间复杂度
- 时间复杂度是对一个算法运行时间长短的量度,用大O表示,记作T(n)=O(f(n))
- 常见的时间复杂度按照从低到高的顺序,包括O(1)、O(logn)、O(n)、O(nlogn)、O(n^2)等。
- 什么是空间复杂度
- 空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度,用大O表示,记作S(n)=O(f(n))
- 常见的空间复杂度按照从低到高的顺序,包括O(1)、O()、O(n)等。其中递归算法的空间复杂度和递归深度成正比。