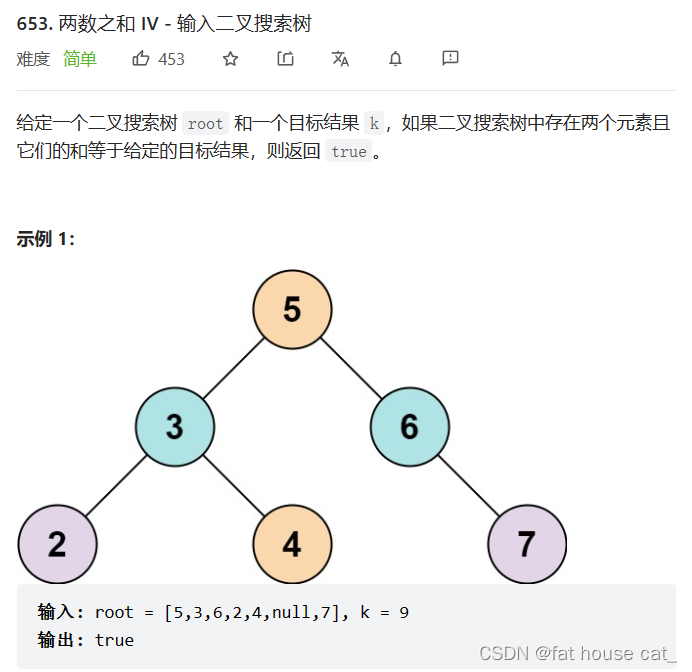
---

 法一：深度搜索+中序遍历+双指针

思路：通过中序遍历二叉树得到一个递增的数列，再在这个递增的二叉树中找到这两数。

主要学到双指针这个方法。

对于一般数列，我们要找到两数满足其之和等于目标数，我们一般会进行暴力，即两重循环：

for(i=0;i<length;i++){
    for(j=i+1;j<length;j++){

    }
}

 对于暴力，我们要把下图的空白格全都依次检验，贼费时间。

---

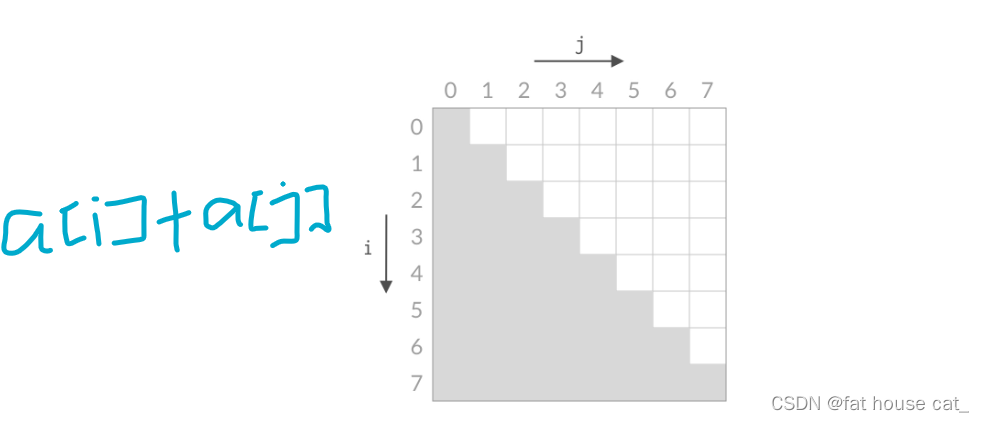
 而如果设置双指针，对应 i 和 j ，分别指向数组的头和尾。

如果a[0]+a[7]<target,说明a[0]+a[1]，a[0]+a[2]，a[0]+a[3]，a[0]+a[4].....全都不满足，我们就可以直接把a[0]+的所有数给全部排除。 即把i=0时的那一排全排除了。

如果a[0]+a[7]>target,说明a[1]+a[7]，a[2]+a[7]，a[3]+a[7]......全不满足，我们就可以把j=7的那一列全排除了。

总结就是 i 是指向数组头的指针，如果i 右移，则删排，j 是指向数组尾的指针，如果j 左移，则删列。

这是缩减搜索空间的思想。

题解参考一张图告诉你 O(n) 的双指针解法的本质原理（C++/Java） - 两数之和 II - 输入有序数组 - 力扣（LeetCode）

---

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
void inorderTraversal(const struct TreeNode* node, int* vec, int* pos) {
    if (node == NULL) {
        return;
    }
    inorderTraversal(node->left, vec, pos);
    vec[(*pos)++] = node->val;
    inorderTraversal(node->right, vec, pos);
}

bool findTarget(struct TreeNode* root, int k) {
    int * vec = (int *)malloc(sizeof(int) * 10000);
    int pos = 0;
    inorderTraversal(root, vec, &pos);
    int left = 0, right = pos - 1;
    while (left < right) {
        if (vec[left] + vec[right] == k) {
            return true;
        }
        if (vec[left] + vec[right] < k) {
            left++;
        } else {
            right--;
        }
    }
    free(vec);
    return false;
}