知识表示
one-hot representation: 将研究对象表示为向量,该向量只有某一维度非零,其他维度上的值均为零。独热表示是信息检索和搜索引擎中广泛使用的词袋模型的基础,优点是无需学习过程。简单高效,在信息检索和自然语言处理中得到广泛应用。缺点是会丢失大量有用的信息。无法有效的表示短文本。容易受到数据稀疏问题的影响。
表示学习的目标:通过机器学习将研究对象的语义信息表示为稠密低维实质向量。将实体
e
e
e和关系
r
r
r表示为两个不同的向量。在向量空间中,通过欧氏距离和余弦距离等方式。计算任意两个对象之间的语义相似度。
传统的知识表示方法主要以RDF,资源描述框架的三元组
S
P
O
SPO
SPO(subject,property,object)来符号性的描述实体之间的关系。这种表示方法通常使用简单,受到广泛的认可。但在计算效率、数据稀疏方面受到存在诸多问题。近年来,以深度学习为代表的表示学习取得了重要的进展。可以将实体的语义信息表示为稠密低维实值向量。进而在低维空间中高效计算实体、关系及其之间的复杂语义关联。对知识库的构建、推理、融合以及应用均有重要的意义。
符号
使用
G
=
(
E
,
R
,
T
)
G = (E,R,T)
G=(E,R,T)来表示完整的知识图谱,其中
E
E
E = {
e
1
,
e
2
,
⋯
,
e
∣
E
∣
e_1,e_2,\cdots,e_{|E|}
e1,e2,⋯,e∣E∣}表示实体集合。
R
=
(
r
1
,
r
2
,
⋯
,
r
∣
R
∣
)
R = (r_1,r_2,\cdots,r_{|R|})
R=(r1,r2,⋯,r∣R∣)表示关系集合。
T
T
T表示三元组集合。
∣
E
∣
|E|
∣E∣和
∣
R
∣
|R|
∣R∣表示实体和关系的数量。
知识图谱以三元组
<
h
,
r
,
t
>
<h,r,t>
<h,r,t>的形式表示,其中
h
∈
E
h \in E
h∈E表示头实体,
t
∈
E
t \in E
t∈E表示尾实体,
r
∈
R
r \in R
r∈R表示
h
和
t
h和t
h和t之间的关系集合。
SE
SE(Structured Embedding)会将每个实体投影到
d
d
d维空间向量。具体来说,SE会为每个关系设计两个矩阵
M
r
,
1
和
M
r
,
2
∈
R
d
×
d
M_{r,1}和M_{r,2} \in R^{d \times d}
Mr,1和Mr,2∈Rd×d,然后使用这两个矩阵将头实体和尾巴实体投影到相同的语义空间中。并计算相似度,SE的评分函数为:
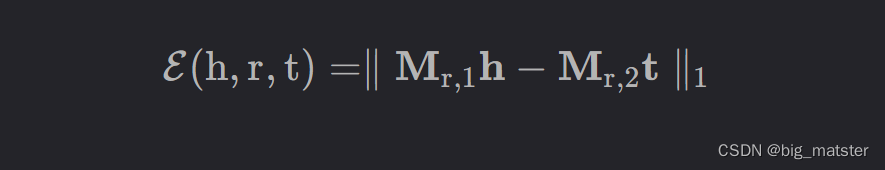
其中
h
,
t
h,t
h,t都会被投影到相应的关系空间中。
不同于TransE 这样基于翻译的模型,SE 会将实体建模为嵌入向量,关系建模为投影矩阵。
距离模型能够利用学习到的知识表示进行链接预测,即通过计算,找到让两实体距离最近的关系矩阵。
距离模型的缺陷**:协同性差,无法精确刻画两个实体之间的语义联系**
论文中关于SE介绍
SE: 一种直观的基于距离的方法是计算实体在关系的对应空间中的投影向量之间的距离。结构表示为(structured embedding, SE[).中每个实体用
d
d
d维向量表示,SE为每个关系定义了两个投影矩阵,
M
r
,
1
M
r
,
2
M_{r,1} M_{r,2}
Mr,1Mr,2 利用这两个投影矩阵和
L
1
L_1
L1距离学习结构嵌入为:

该距离表明头实体
h
h
h和尾实体
t
t
t在关系
r
r
r的语义相关度。然而SE对头尾实体使用2个不同的矩阵进行投影,因此SE的协同性较差,无法精确的刻画画头、尾实体与关系之间语义联系的强弱.。