题目来源
222. 完全二叉树的节点个数

递归法

递归三步曲

• 1.确定递归函数的参数和返回值
  参数就是传入树的根节点，返回就返回以该节点为根节点二叉树的节点数量，所以返回值为int类型。

int countNodes(TreeNode root)

• 2.确定终止条件

如果为空节点的话，就返回0，表示节点数为0。

        if(root == null){
            return 0;
        }

• 3.确定单层递归的逻辑

先求它的左子树的节点数量，再求右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。

        int leftNum  = countNodes(root.left);
        int rightNum  = countNodes(root.right);
        int treeNum = leftNum + rightNum + 1;
        return treeNum;

整体代码如下

改进

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。
举一个典型的例子如题：

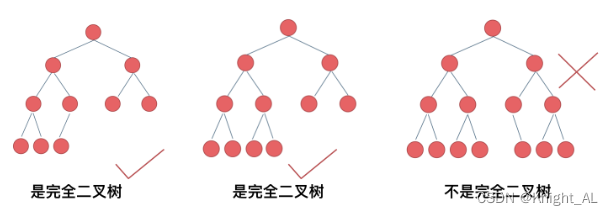
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。
对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。
对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。
像这种就可以不用进入递归，直接返回(2 << leftDepth) - 1

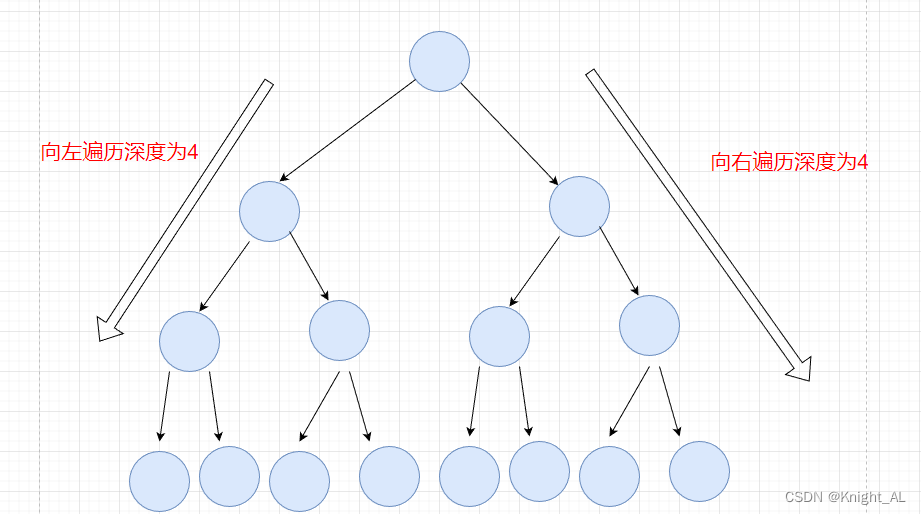
class Solution {
    public int countNodes(TreeNode root) {
        if(root == null){
            return 0;
        }
        TreeNode left = root.left;
        TreeNode right = root.right;
        int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
        while(left!=null){
            left = left.left;
            leftDepth++;
        }
        while (right!=null) { // 求右子树深度
            right = right.right;
            rightDepth++;
        }
        if(leftDepth == rightDepth){
            return (2 << leftDepth) - 1;
        }
        int leftNum  = countNodes(root.left);
        int rightNum  = countNodes(root.right);
        int treeNum = leftNum + rightNum + 1;
        return treeNum;
    }

}