文章目录
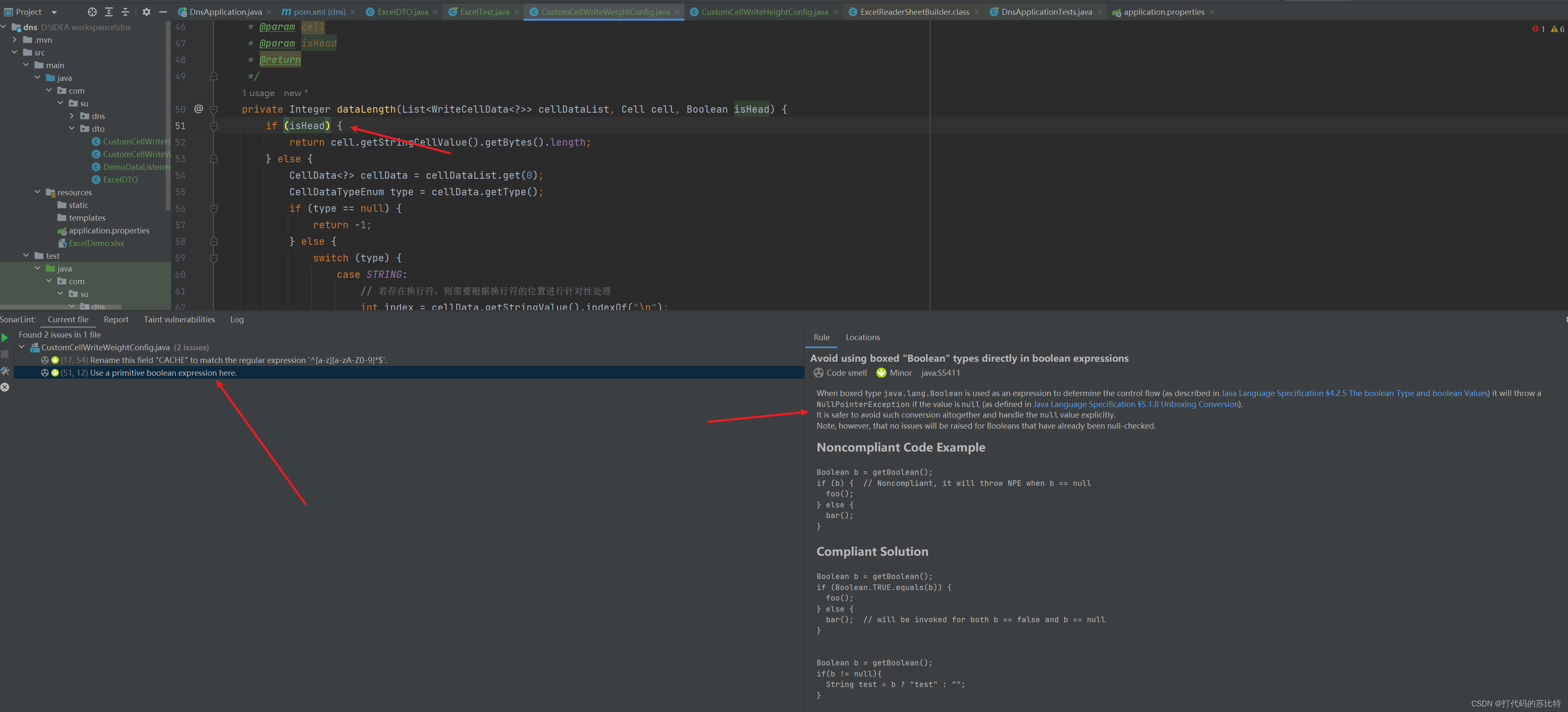
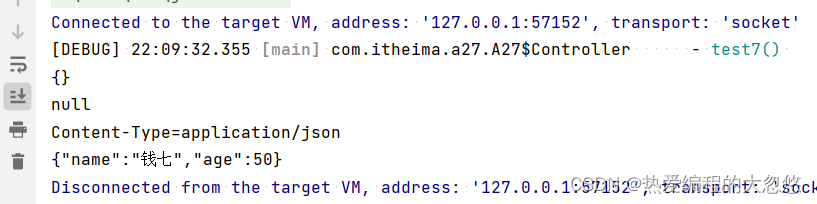
- 1. 写代码
- 2. 写文案
- 3. 写剧本
- 4. 写歌诗
- 5. 写报告
- 6. 查公式
- 7. 写对联
- 8. 写文章
- 9. 做表格
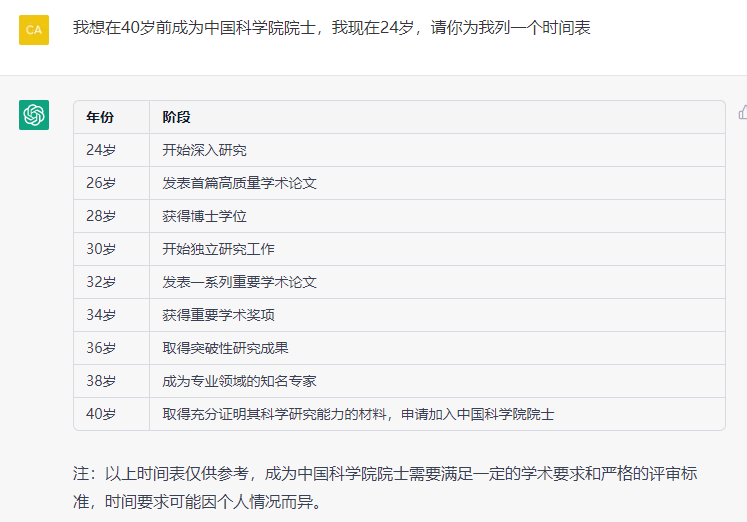
- 10. 做计划
- 11. 等等
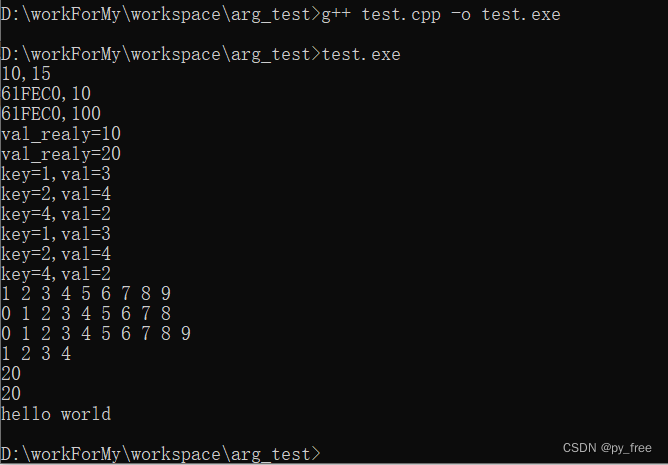
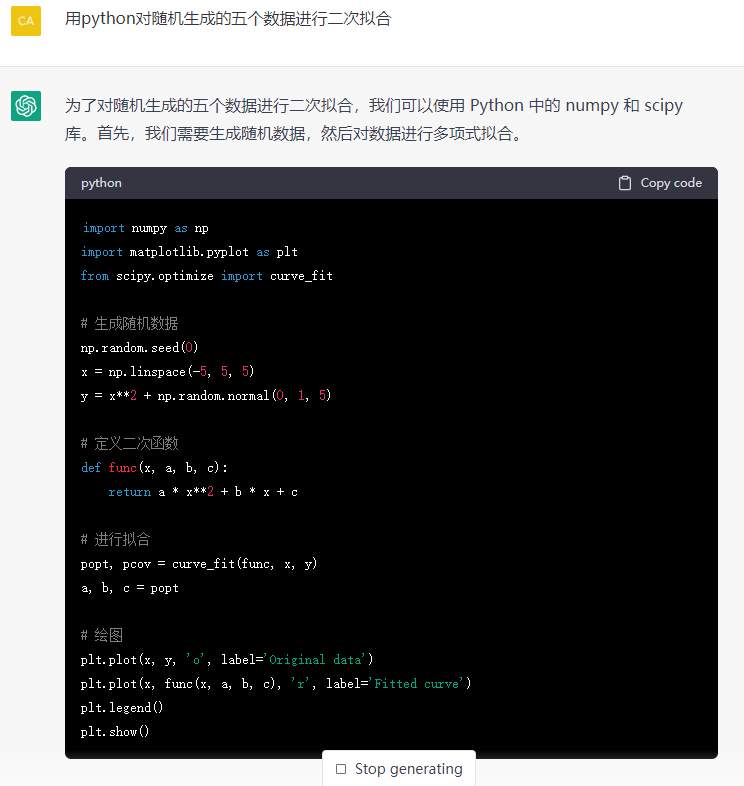
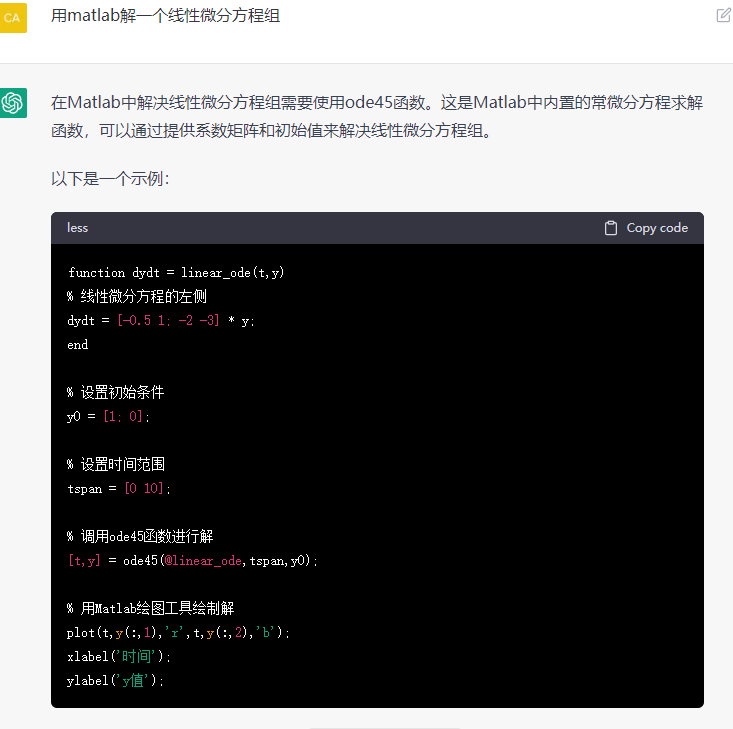
1. 写代码


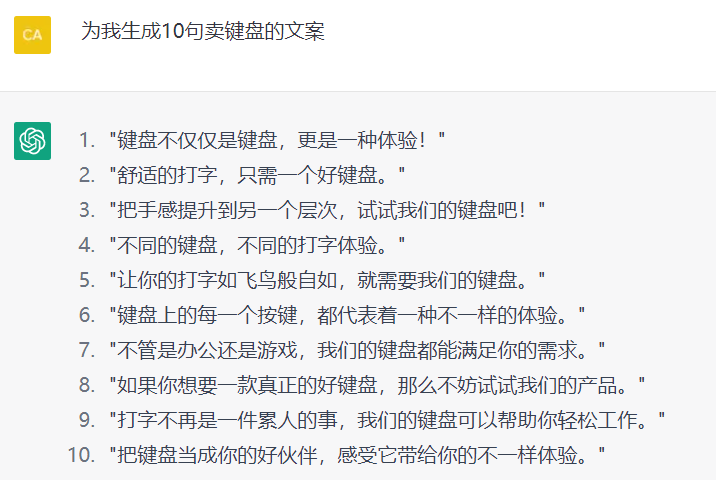
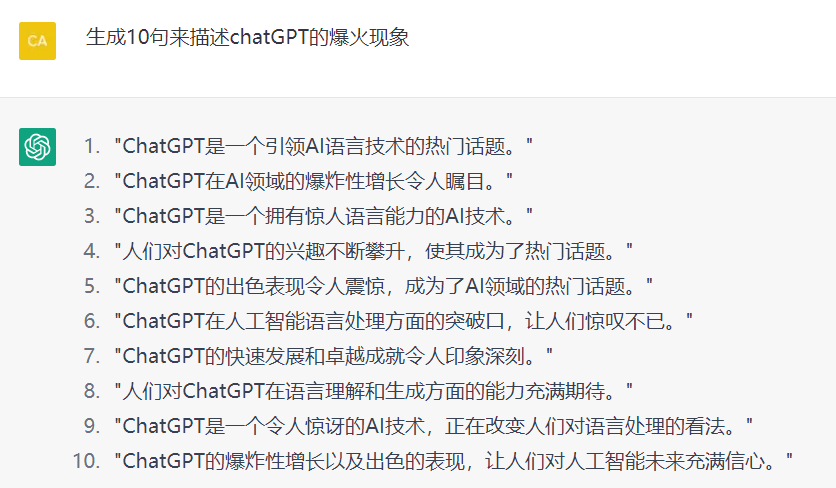
2. 写文案

3. 写剧本


4. 写歌诗
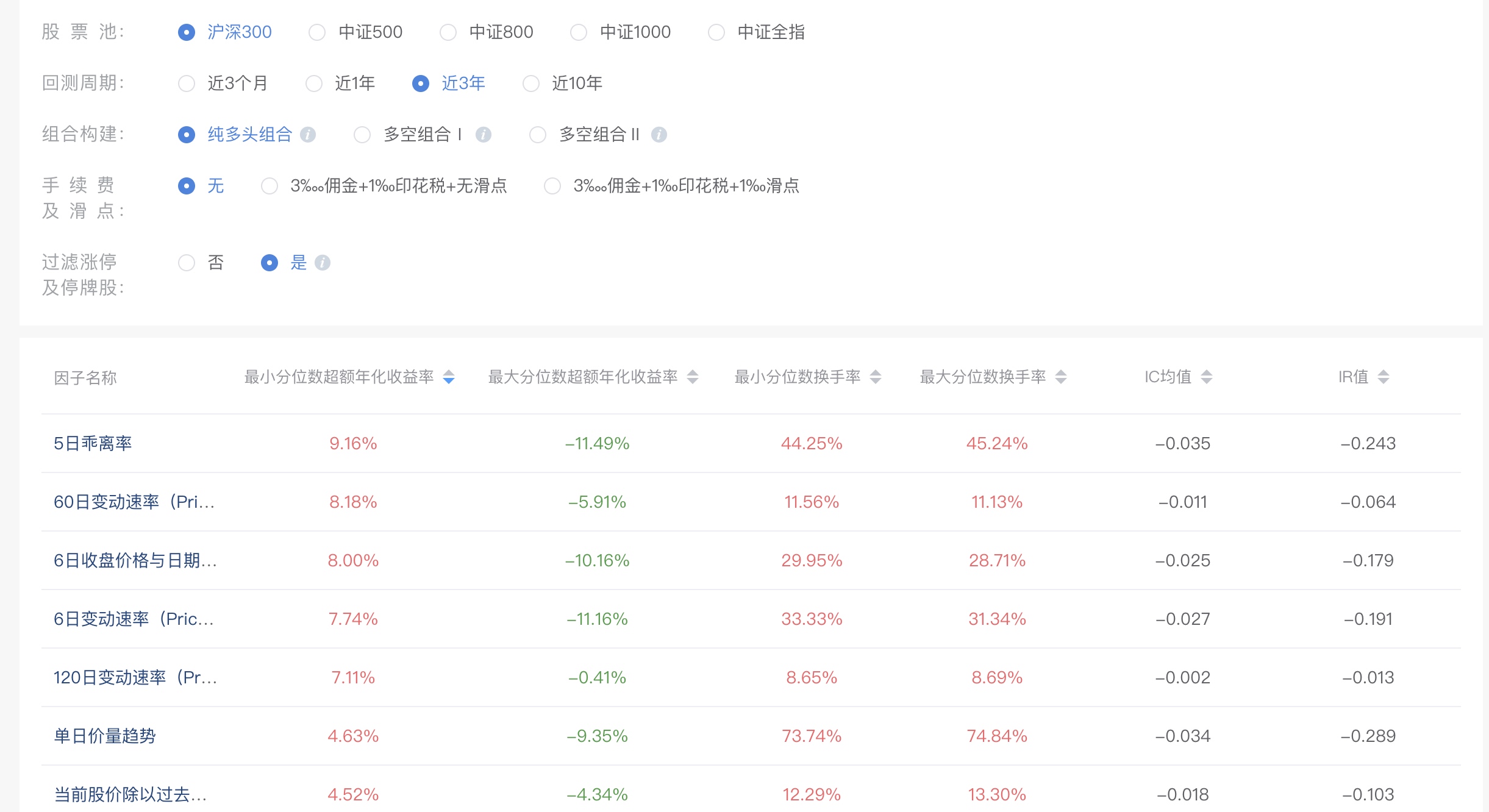
5. 写报告

这妥妥的翻译文,数据完全不对。


6. 查公式

傅里叶变换的时域性质有如下几点:
对称性: F ( f ( t ) ) = F ( f ( − t ) ) ∗ \mathcal{F}(f(t)) = \mathcal{F}(f(-t))^* F(f(t))=F(f(−t))∗
循环卷积: F ( f ( t ) ∗ g ( t ) ) = F ( f ( t ) ) ⋅ F ( g ( t ) ) \mathcal{F}(f(t)\ast g(t)) = \mathcal{F}(f(t)) \cdot \mathcal{F}(g(t)) F(f(t)∗g(t))=F(f(t))⋅F(g(t))
时间平移: F ( f ( t − t 0 ) ) = e − j 2 π f 0 t 0 F ( f ( t ) ) \mathcal{F}(f(t-t_0)) = e^{-j2\pi f_0t_0} \mathcal{F}(f(t)) F(f(t−t0))=e−j2πf0t0F(f(t))
时间拓展: F ( α f ( t ) ) = 1 ∣ α ∣ F ( f ( t α ) ) \mathcal{F}(\alpha f(t)) = \frac{1}{|\alpha|} \mathcal{F}(f(\frac{t}{\alpha})) F(αf(t))=∣α∣1F(f(αt))
时间反转: F ( f ( − t ) ) = F ( f ( t ) ) ∗ \mathcal{F}(f(-t)) = \mathcal{F}(f(t))^* F(f(−t))=F(f(t))∗
以上是傅里叶变换的时域性质,其中,
F
\mathcal{F}
F 表示傅里叶变换,
f
(
t
)
f(t)
f(t) 和
g
(
t
)
g(t)
g(t) 是时域信号,
∗
\ast
∗ 表示循环卷积,
∗
^*
∗ 表示复共轭,
f
0
f_0
f0 是信号的频率,
t
0
t_0
t0 是时间平移量,
α
\alpha
α 是时间拓展量。

设原始的两个高斯分布分别为
f
(
x
)
f(x)
f(x) 和
g
(
x
)
g(x)
g(x),每个分布的平均值分别为
μ
1
\mu_1
μ1 和
μ
2
\mu_2
μ2,标准差分别为
σ
1
\sigma_1
σ1 和
σ
2
\sigma_2
σ2。
那么两个高斯分布相加后的结果为:
f
(
x
)
+
g
(
x
)
=
1
2
π
σ
1
e
−
(
x
−
μ
1
)
2
2
σ
1
2
+
1
2
π
σ
2
e
−
(
x
−
μ
2
)
2
2
σ
2
2
f(x) + g(x) = \frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{(x-\mu_1)^2}{2\sigma_1^2}} + \frac{1}{\sqrt{2\pi}\sigma_2}e^{-\frac{(x-\mu_2)^2}{2\sigma_2^2}}
f(x)+g(x)=2πσ11e−2σ12(x−μ1)2+2πσ21e−2σ22(x−μ2)2通过简单的数学计算,得到这个结果的平均值
μ
\mu
μ 和标准差
σ
\sigma
σ 为:
μ
=
μ
1
σ
2
2
+
μ
2
σ
1
2
σ
1
2
+
σ
2
2
\mu = \frac{\mu_1\sigma_2^2 + \mu_2\sigma_1^2}{\sigma_1^2 + \sigma_2^2}
μ=σ12+σ22μ1σ22+μ2σ12
σ
=
σ
1
2
σ
2
2
σ
1
2
+
σ
2
2
\sigma = \sqrt{\frac{\sigma_1^2\sigma_2^2}{\sigma_1^2 + \sigma_2^2}}
σ=σ12+σ22σ12σ22

用
f
(
t
)
f(t)
f(t) 表示门函数,用
g
(
t
)
g(t)
g(t) 表示辛格函数,卷积的结果为:
(
f
∗
g
)
(
t
)
=
∫
−
∞
∞
f
(
τ
)
g
(
t
−
τ
)
d
τ
(f*g)(t)=\int_{-\infty}^\infty f(\tau)g(t-\tau)d\tau
(f∗g)(t)=∫−∞∞f(τ)g(t−τ)dτ由于
f
(
t
)
f(t)
f(t) 是一个门函数,其具有以下形式:
f
(
t
)
=
{
1
,
t
∈
[
−
1
2
,
1
2
]
0
,
t
∉
[
−
1
2
,
1
2
]
f(t)=\begin{cases} 1, & t\in[-\frac{1}{2},\frac{1}{2}] \ 0, & t\notin[-\frac{1}{2},\frac{1}{2}] \end{cases}
f(t)={1,t∈[−21,21] 0,t∈/[−21,21]
g
(
t
)
g(t)
g(t) 是一个辛格函数,其具有以下形式:
g
(
t
)
=
sinc
(
t
)
=
sin
(
π
t
)
π
t
g(t)=\text{sinc}(t)=\frac{\sin(\pi t)}{\pi t}
g(t)=sinc(t)=πtsin(πt)代入卷积的结果中:
(
f
∗
g
)
(
t
)
=
∫
−
1
2
1
2
sin
(
π
(
t
−
τ
)
)
π
(
t
−
τ
)
d
τ
(f*g)(t)=\int_{-\frac{1}{2}}^{\frac{1}{2}}\frac{\sin(\pi (t-\tau))}{\pi (t-\tau)}d\tau
(f∗g)(t)=∫−2121π(t−τ)sin(π(t−τ))dτ因为
sin
\sin
sin 函数的周期性,可以得到:
(
f
∗
g
)
(
t
)
=
1
π
∫
−
1
2
1
2
sin
(
π
t
)
t
−
τ
d
τ
(f*g)(t)=\frac{1}{\pi}\int_{-\frac{1}{2}}^{\frac{1}{2}}\frac{\sin(\pi t)}{t-\tau}d\tau
(f∗g)(t)=π1∫−2121t−τsin(πt)dτ以上是卷积的结果,具体的数值可以用其他方法来计算,如变量变换或数学公式的计算。
7. 写对联



8. 写文章
写文章这块有个问题就是,生成英文的话不管多少字都可以直接给出,而中文就非常受限。


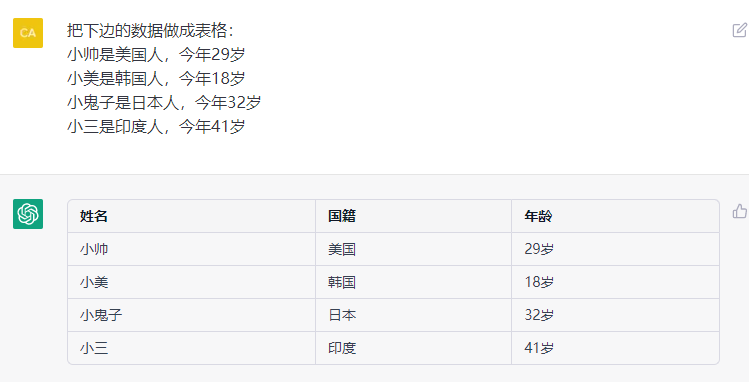
9. 做表格

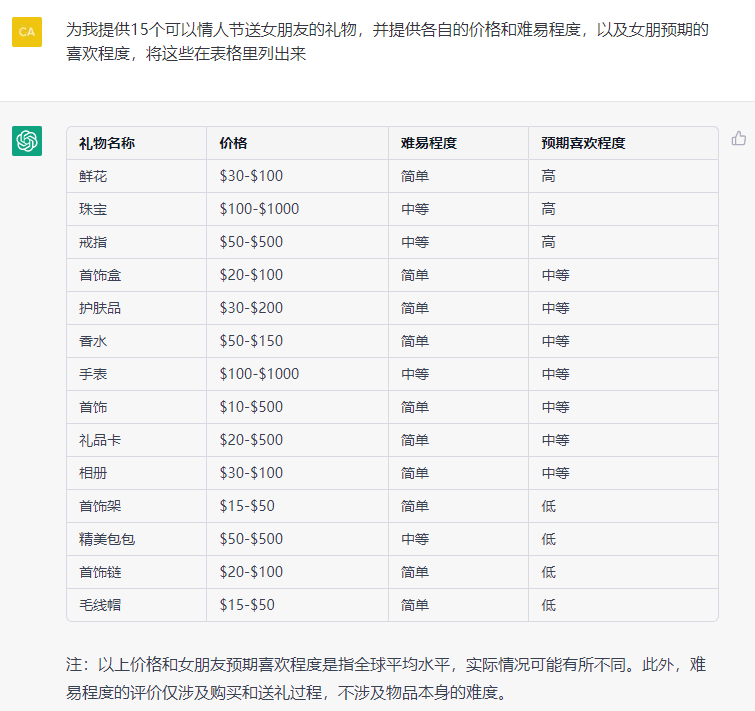
10. 做计划