代码随想录算法训练营第二十七天|● 39. 组合总和 ● 40.组合总和II ● 131.分割回文串

news2025/1/10 3:16:14

39. 组合总和

看完题后的思路

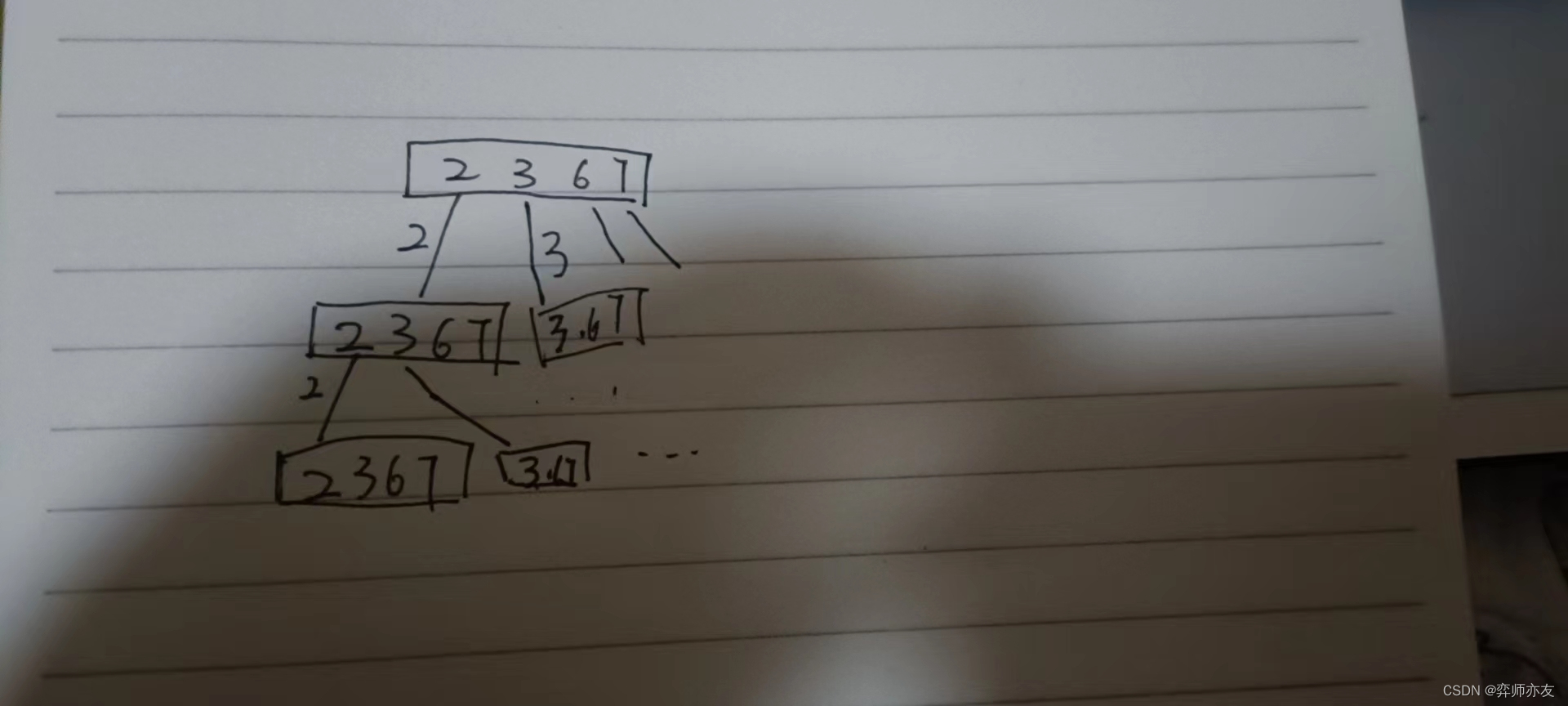
在这里插入图片描述

本题本质上还是一个传统排列题，不同之处在于每个元素可以重复选取。
void f（【】，startIndex，sum）
递归终止
if（和==target）{
加入；
返回；
}
递归
for（）{
剪枝；
加入；
f（xxx，startIndex）；// 不变
回溯；
// 本层下一个

}
4. 剪枝
使用continue；

代码

class Solution {
        List<List<Integer>> ires = new ArrayList<>();
    ArrayList<Integer> ipath = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        combinationSumBT(candidates,target,0,0);
        return ires;
    }
    public void combinationSumBT(int[] candidates, int target,int sum,int startIndex) {
        // 出口
        if (sum==target){
            ires.add(new ArrayList<>(ipath));
            return;
        }
        
        // 引擎
        for (; startIndex < candidates.length; startIndex++) {
            // 剪枝
            if (candidates[startIndex]+sum>target){
                    continue;
            }
            ipath.add(candidates[startIndex]);
            combinationSumBT(candidates,target,sum+candidates[startIndex],startIndex);
            ipath.remove(ipath.size()-1);
            // 下一次
        }
       
    }
}

复杂度

最坏 0（元素个数^target）,最深target层
在这里插入图片描述

收获

1. 三刷大脑过一遍
2. 本题是组合取重复元素

40.组合总和II

看完题后的思路

在这里插入图片描述

本题是组合问题，元素有重复，结果中元素可以重复，但是要对重复的结果去重

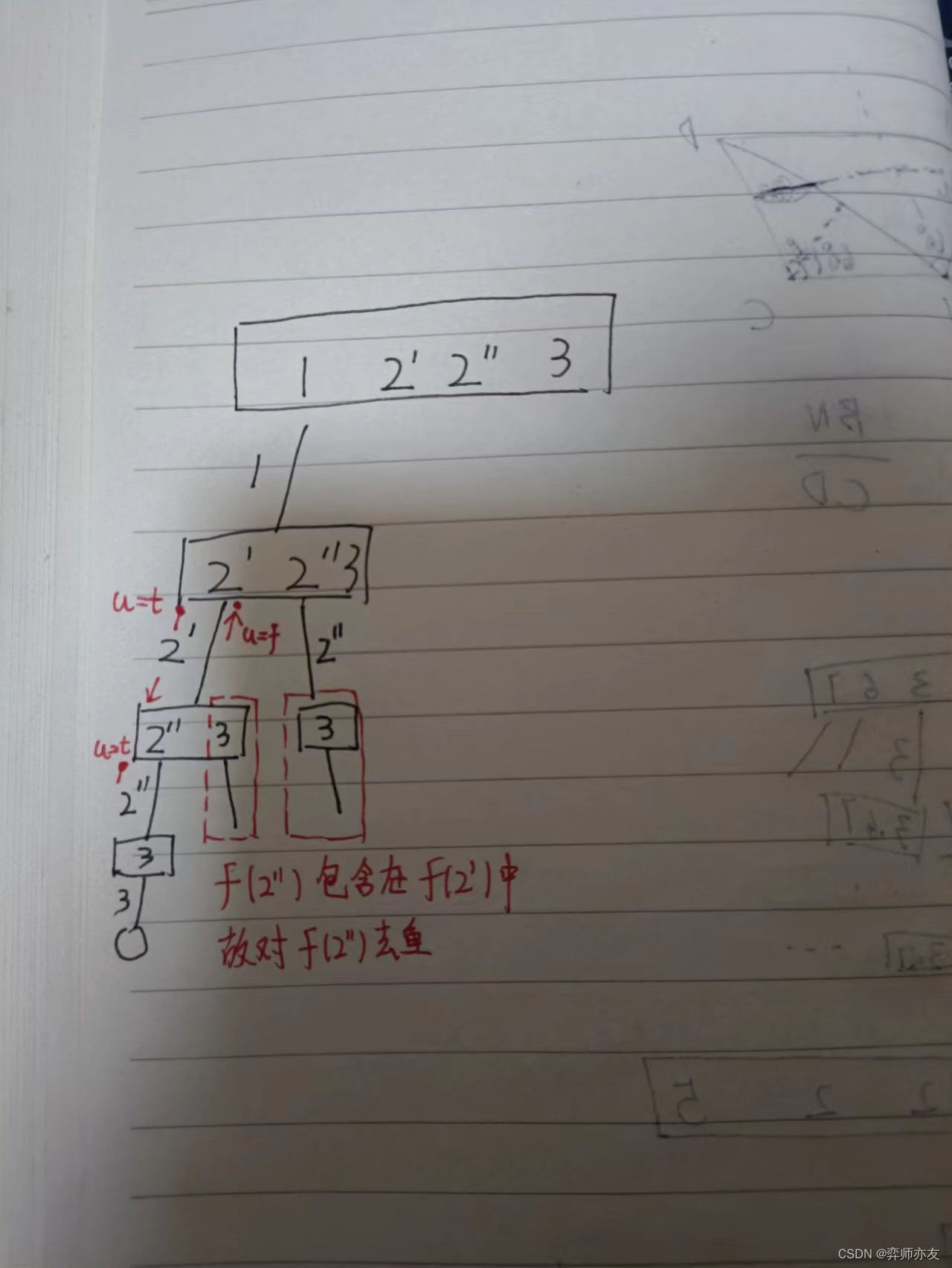
需改处：同一层中，本元素如果与上一个元素相等，直接剪枝。
难点：如何判断是本层还是下一层
层去重的逻辑：
using：表示尚在使用
初始using=false，当使用到我（加入数组），using=ture，执行完成，回溯时，using=false；
如果我前面的节点与我相同:
（1）using[前面的节点]=false;表示我前面的节点已经使用完回溯了，或者压根没用上
对于已经回溯完：我的结果肯定包含在前面结果中，所以我跳过
对于没用上，它被剪枝了，我俩一样，也肯定被剪枝
（2）using[前面的节点]=ture；它一定在我前面，且正在使用，我一定是它的子节点。

代码

class Solution {
     List<List<Integer>> ires = new ArrayList<>();
    ArrayList<Integer> ipath = new ArrayList<>();
  public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        boolean[] using = new boolean[candidates.length];
        Arrays.sort(candidates);
        combinationSum2BT(candidates,target,0,0,using);
        return ires;
    }

    public void combinationSum2BT(int[] candidates, int target,int sum,int startIndex,boolean[] using) {// using[] 是否正在使用
        // 出口
        if (sum==target){
            ires.add(new ArrayList<>(ipath));
            return;
        }

        // 引擎
        for (; startIndex < candidates.length; startIndex++) {
            // 剪枝
            if (candidates[startIndex]+sum>target){
                return; // 因为是拍好序的
            }
            if (startIndex!=0&&candidates[startIndex-1]==candidates[startIndex]&&!using[startIndex-1]){
                continue;
            }
            
            using[startIndex]=true;
            ipath.add(candidates[startIndex]);
            combinationSum2BT(candidates,target,sum+candidates[startIndex],startIndex+1,using);

            // 回溯
            using[startIndex]=false;
            ipath.remove(ipath.size()-1);
            // 下一次
        }

    }

}

复杂度

在这里插入图片描述

收获

1. 三刷看一遍
2. 横向去重

131.分割回文串

这是一个标准切割问题
v f（【】，startIndex）
出口 if（startIndex==数组长度）{加入，return}
回溯
与标准模板不同 ipath.add([].子串（startIndex，i）)
剪枝
不是回文串 continus
直接看代码

代码

class Solution {
 List<List<String>> sres = new ArrayList<>();
    ArrayList<String> spath = new ArrayList<>();
    public List<List<String>> partition(String s) {
        partitionBT(s,0);
        return sres;
    }

    public void partitionBT(String s,int startIndex) {
        if (startIndex==s.length()){
            sres.add(new ArrayList<>(spath));
            return;
        }
        // 引擎
        for (int i = startIndex; i <s.length() ; i++) {
            // 剪枝
            if (!isPalindrome(s,startIndex,i)){
                 continue;
            }
            spath.add(s.substring(startIndex,i+1));
            partitionBT(s,i+1);
            spath.remove(spath.size()-1);
            // 本层下一个
        }
    }

    //判断是否是回文串
    private boolean isPalindrome(String s, int startIndex, int end) {
        for (int i = startIndex, j = end; i < j; i++, j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        return true;
    }
}