0. 简介

对于自动驾驶的预测和规划而言，能够有效的对目标产生可解释性是非常有必要的，而《Interpretable Goal-based Prediction and Planning for Autonomous Driving》文中就提出了一种综合的自动驾驶预测和规划系统，它利用合理的逆规划来识别其他车辆的意图。目标识别可以通过蒙特卡罗树搜索(MCTS)算法来规划自我车辆的最佳动作。逆规划和MCTS利用一组共同定义的动作和宏观行动来构建可通过理性原则来解释的规划。对城市驾驶场景模拟的评估表明，该系统能够稳健地识别其他车辆的意图，使我们的车辆能够利用重要的机会来显著减少驾驶时间。难能可贵的是这篇文章是开源的，对应的代码在Github上。同时该文件也存在有官网供读者学习：https://www.five.ai/igp2

1. 文章贡献

本文提出了基于可解释目标的预测和规划(IGP2)，它利用了使用有限空间意图(maneuvers)的计算优势，但扩展了该方法到意图序列(即计划)的规划和预测。**我们通过一种新颖的整合理性逆向规划[23]、[24]来识别其他车辆的目标，并通过蒙特卡罗树搜索(MCTS)[25]来为自我车辆规划最优意图。**逆向规划和MCTS利用一组已定义的操作来构建计划，这些计划可以通过合理性原则来解释，即计划相对于给定的度量是最优的。作者在不同城市驾驶场景的模拟中评估了IGP2，表明(1)即使车辆轨迹的重要部分被遮挡，该系统也能稳健地识别其他车辆的目标;(2)目标识别使我们的车辆能够利用机会提高驾驶效率(与其他预测基线相比，通过驾驶时间来衡量);(3)我们能够提取预测的直观解释，以证明系统的决策是合理的。为此本文的主要贡献有以下三点：

1. 提出了一种基于有理逆规划的目标识别和多模态轨迹预测方法。
2. 整合目标识别与MCTS规划，为自我车辆生成优化后的轨迹。
3. 在模拟城市驾驶场景中进行评估，从而显示目标识别准确率，驾驶效率等表现的提高，以及解释预测和自我规划的能力。

2. 详细内容

我们的一般方法依赖于两个假设:(1)每辆车都试图从一组可能的目标中达到某个(未知)目标;(2)每辆车都遵循由有限的已定义机动库生成的计划。

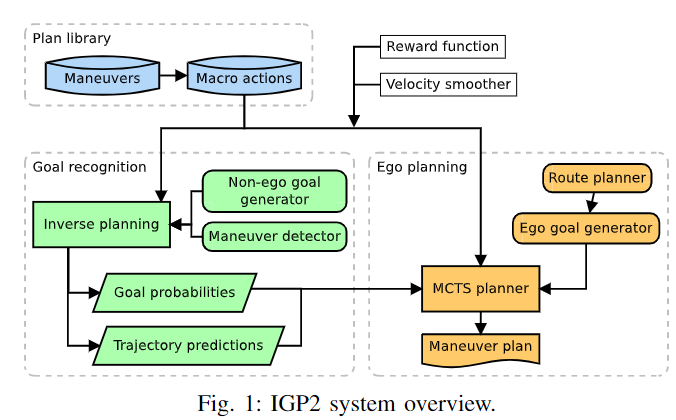
下图展示了本文提出的IGP2系统中组件的概述。在较高的水平上，IGP2近似于最优自我策略$\pi \ast$的表现:对于每个非自我载体，生成其可能的目标，并为该载体进行实现每个目标的逆向规划。每个非自我车辆的目标概率和预测轨迹为蒙特卡罗树搜索(MCTS)算法的模拟过程提供信息，为自我车辆生成朝着当前目标前进的最佳机动计划。为了在逆向规划和MCTS中保持所需的搜索深度较浅(因此有效)，两者都在一组共享的宏动作上进行规划，这些宏动作使用上下文信息灵活地连接机动。

2.1 意图

我们假设在任何时候，每辆车都在执行下列操作之一: 车道跟随、车道变换、左/右、转左/右、让路、停车。每个意图$\omega$指定适用性和终止条件。 例如，只有当车辆的左侧有一条与其行驶方向相同的车道时，才适用变道左行，并在车辆到达新车道及其方向与该车道一致时终止。一些意图有自由参数，例如，跟随车道有一个参数来指定何时终止。

如果适用的话，意图就会指定车辆要遵循的局部轨迹${\hat{s}}_{1:n}^i$，其中包括全局坐标框架中的参考路径和沿路径的目标速度。为了论述的方便，我们假设${\hat{s}}^i$使用与$s^i$相同的表示和索引，但在一般情况下不一定是这样的（例如，$\hat{s}$ 可以用纵向位置而不是时间来索引，它可以插值为时间索引）。在我们的系统中，参考路径是通过一个贝塞尔样条函数与一组从道路拓扑结构中提取的点相拟合而产生的，目标速度是用类似于[27]的领域启发式方法设置的。

2.2 宏观行为

宏观动作指定了常见的动作序列，并根据上下文信息（如道路布局）自动设置动作中的自由参数（如果有的话）。表一列出了我们系统中使用的宏动作。宏观动作的适用性条件由宏观动作中第一个意图的适用性条件以及可选的附加条件给出。宏观行动的终止条件是由宏观行动中最后一个动作的终止条件给出的。

2.3 速度平滑

为了获得车辆$i$的可行的意图的轨迹，我们定义了一个速度平滑操作，优化给定轨迹中的目标速度${\hat{s}}_{1:n}^i$。设 ${\hat{x}}_t$ 为参考轨迹上的纵向位置，当$1\le t\le n$ 时，${\hat{v}}_t$ 为目标速度。我们将 $\kappa :x\to v$ 定义为目标速度在 ${\hat{x}}_t$ 点之间的分段线性插值。给定两个时间步骤之间经过的时间$\Delta t$; 最大速度和加速度$v_{max}/a_{max}$; 设置 $x_1=\hat{}{x}_1，v_1={\hat{v}}_1$，我们将速度平滑定义为

…详情请参照古月居