343 整数拆分 medium
给定一个正整数
n,将其拆分为k个 正整数 的和(k >= 2),并使这些整数的乘积最大化。返回 你可以获得的最大乘积 。
这道题乍一看没有点儿动态规划的影子,反而感觉用数学法可以求解。
但是,既然放在了动态规划的范畴里,还是有其可取巧的成分,因为一个数字要拆分,像是后面要提到的背包问题,所以想想应该怎么求解。
还是五部曲,
1 - 确定dp数组:如果是卡的话,大多就卡在这一步和下一步,如果看成背包问题就好想那么一点,那么dp[i] 就可以表示 i 拆分完之后的最大乘积。
2 - 确定递推公式:这道题既不是此前的一维数组,也不是二维数组。我们可以想一下,如果要得到 i 的最大乘积,那么结果必然是从某个乘式而来,先考虑两个数相乘,可以从1到 j 遍历,乘积为 j x (i - j),再考虑多个数相乘,可以用j x dp(i - j)表示
我们以n = 4为例,dp[1] = 1, dp[2] = 1x2 = 2, dp[3] = 1 x 2 = 2
而dp[4] = 2 x 2 = 4, 先从max(1x3, 1xdp[3])考虑,再计算2x2,最终结果还是2x2比较大。
3 - 确定初始化:上一步中就确定了初始化的结果
4 - 遍历顺序:第二步中也分析了
5 - 举例:参考第二步
根据以上思想,代码如下:
int integerBreak(int n) {
vector<int> dp(n + 1, 0);
dp[2] = 1;
for (int i = 3; i <= n; ++i) {
for (int j = 1; j <= i/2; ++j) {
dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]));
}
}
return dp[n];
}
数学法,此处不证明,具体证明过程可以参考本题LeetCode的官方解法,代码如下:
int integerBreak(int n) {
if (n <= 3) {
return n - 1;
}
int quotient = n / 3;
int remainder = n % 3;
if (remainder == 0) {
return (int)pow(3, quotient);
} else if (remainder == 1) {
return (int)pow(3, quotient - 1) * 4;
} else {
return (int)pow(3, quotient) * 2;
}
}
96 不同的二叉搜索树 medium
给你一个整数
n,求恰由n个节点组成且节点值从1到n互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
这道题乍一看还是没什么动态规划的感觉,用暴力搜索感觉反而好做一点。
不过还是试着写一写五部曲:
1 - 确定dp数组:dp[i]就是从1到 i ,不相同的二叉搜索树的个数,注意是二叉搜索树,否则这道题就简单了。
2 - 确定递推公式:这一步比较难想。但是应该还是有规律可寻的。此处借用一下随想录中的两张图片来说明问题,
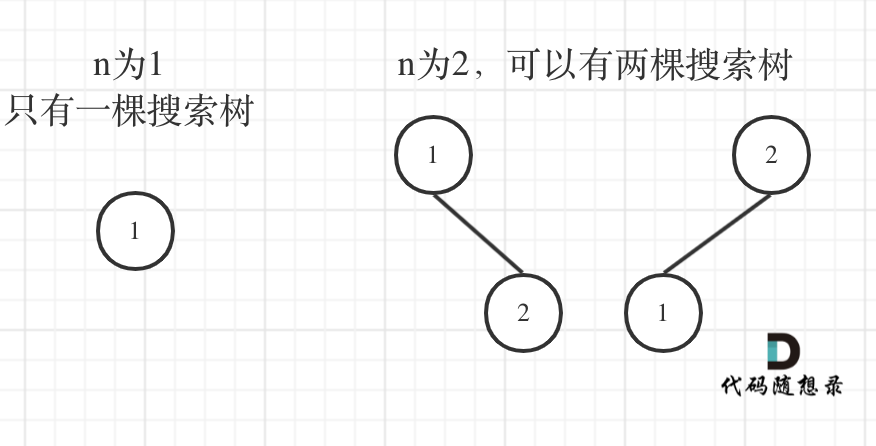
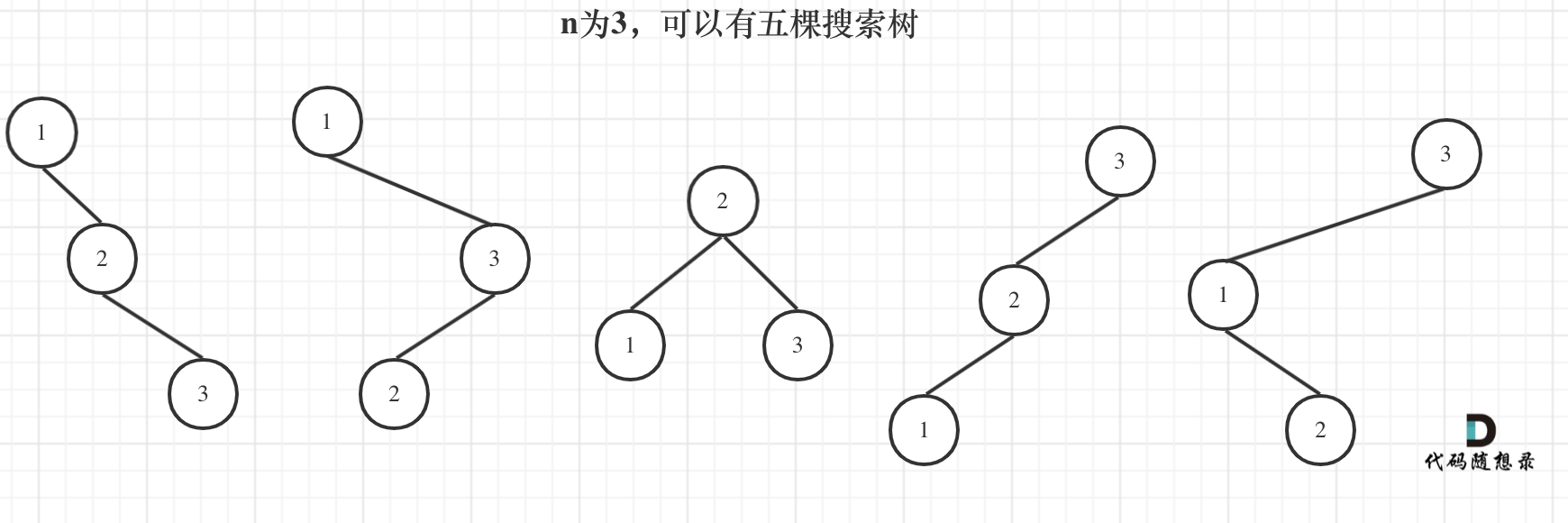
可以看出,当 i = 3的时候,以1为头结点,抛开这个头结点,其结构和 i = 2的时候是一样的;而头结点为2时,左右子树都是一个结点,结构和 i = 1的时候是一样的;而头结点为3的时候,抛开这个头结点,结构和 i = 2是又是一样的。说到这里好像有些规律可寻。但是这道题目怪的地方就在于,我们如果按照下式来写,会发现最后一项没法写。
dp[3] = dp[1] * dp[2] + dp[2] * dp[1] + ?
所以,这道题要这么写,要给 i = 0的时候赋初值,才可以写出来递推公式
dp[3] = dp[0] * dp[2] + dp[1] * dp[1] + dp[2] * dp[0]
可以推导出来,dp[i] += dp[j - 1] * dp[i - j]
3 - 初始化:按照第二步中提到的,要初始化dp[0] = 1
4 - 遍历顺序:二维,从小到大
5 - 举例:省略
根据上述思想,代码如下:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
这道题也有数学方法,成为卡塔兰数,推导公式如下:
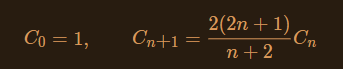
根绝这个式子,代码如下:
int numTrees(int n) {
long long C = 1;
for (int i = 0; i < n; ++i) {
C = C * 2 * (2 * i + 1) / (i + 2);
}
return (int)C;
}