- 论文:《PolyLaneNet: Lane Estimation via Deep Polynomial Regression》
- 代码:https://github.com/lucastabelini/PolyLaneNet
- 地址:https://arxiv.org/pdf/2004.10924.pdf
- 参考:https://blog.csdn.net/sinat_17456165/article/details/107171888
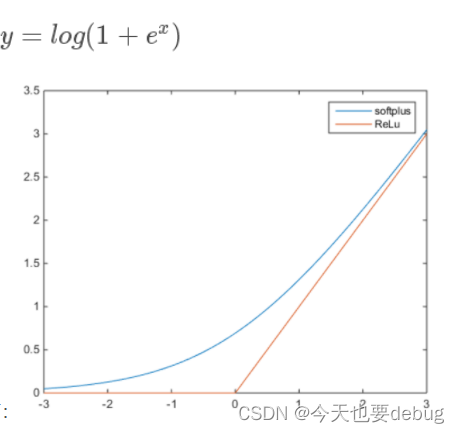
- 利用 CNN,基于三次曲线拟合车道线
模型的输入与输出
输入
单张车辆前向图
输出
曲线参数 P j = { a k , j } k = 0 K \mathcal{P}_j=\{a_{k,j}\}^K_{k=0} Pj={ak,j}k=0K、地平线高度 h h h、车道线的存在性 c j c_j cj、车道线起始高度 s j s_j sj(见下图)
其中,曲线参数确定了车道线的形状:
p j ( y ) = Σ k = 0 K a k , j y k p_j(y)=\Sigma^K_{k=0}a_{k,j}y^k pj(y)=Σk=0Kak,jyk
模型结构

backbone + fully connected layer
f ( I ; θ ) = ( { P j , s j , c j } j = 1 M m a x , h ) f(I;\theta)=(\{\mathcal{P}_j,s_j,c_j\}^{M_{max}}_{j=1}, h) f(I;θ)=({Pj,sj,cj}j=1Mmax,h)
损失函数
L ( { P j } , h , { s j } , { c j } ) = W p L p ( { P j } , { L j ∗ } ) + W s 1 M Σ j L r e g ( s j , s j ∗ ) + W c 1 M Σ j L c l s ( c j , c j ∗ ) + W h L r e g ( h , h ∗ ) \begin{aligned} L(\{\mathcal{P}_j\},h,\{s_j\},\{c_j\})&=W_p L_p(\{\mathcal{P}_j\},\{\mathcal{L}^*_j\})\\&+W_s\frac{1}{M}\Sigma_j L_{reg}(s_j,s^*_j)\\&+W_c\frac{1}{M}\Sigma_j L_{cls}(c_j,c^*_j)\\&+W_h L_{reg}(h,h^*) \end{aligned} L({Pj},h,{sj},{cj})=WpLp({Pj},{Lj∗})+WsM1ΣjLreg(sj,sj∗)+WcM1ΣjLcls(cj,cj∗)+WhLreg(h,h∗)
其中,
L
p
(
{
P
j
}
,
{
L
j
∗
}
)
=
L
r
e
g
(
x
j
,
x
j
∗
)
L_p(\{\mathcal{P}_j\},\{\mathcal{L}^*_j\})=L_{reg}(\pmb{x}_j,\pmb{x}^*_j)
Lp({Pj},{Lj∗})=Lreg(xj,xj∗)
x
j
=
[
x
1
,
j
,
.
.
.
,
x
N
,
j
]
\pmb{x}_j=[x_{1,j},\ ...,\ x_{N,j}]
xj=[x1,j, ..., xN,j]
x
i
,
j
=
{
p
j
(
y
i
,
j
∗
)
,
i
f
∣
p
j
(
y
i
,
j
∗
)
−
x
i
,
j
∗
∣
>
τ
l
o
s
s
0
,
o
t
h
e
r
w
i
s
e
x_{i,j}=\begin{cases}p_j(y^*_{i,j}),\ \ \ \ if\ |p_j(y^*_{i,j})-x^*_{i,j}|>\tau_{loss}\\ 0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ otherwise \end{cases}
xi,j={pj(yi,j∗), if ∣pj(yi,j∗)−xi,j∗∣>τloss0, otherwise
注意这里的0,可以这样理解:设置0之后,就不用计算对应位置的 grad 了。