题目描述

‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素

PATTERN	TRUE	FALSE
a.b	aab,abb,acb	a, ab,b
a*b	b,ab,aab,aaab	a,abb,acb
c*a.b	aab,caab,cccccacb,ccabb	baab,cabbb

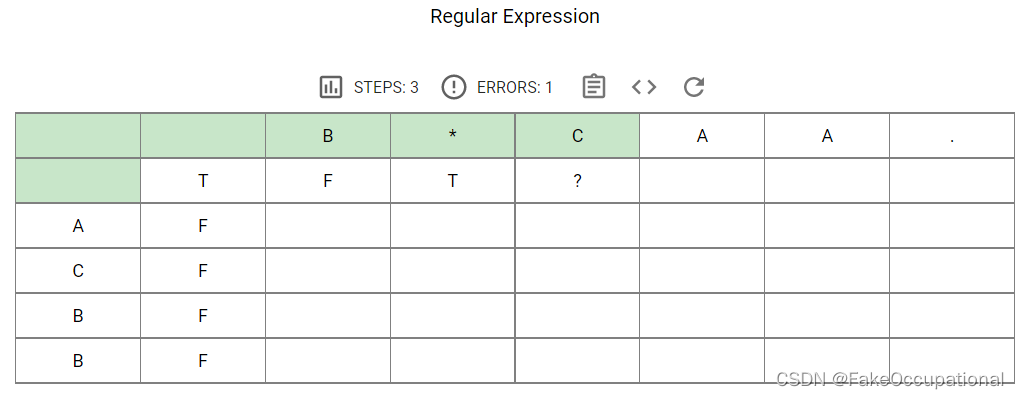
dp[i] [j] 的含义是当字符串 s 的长度为 i，模式串 p 的长度为 j 时，两者是否匹配
同一行往前走两个代表的是 a* 等于空 ,此时， dp[i] [j] = dp[i] [j – 2]
如果当前的字符和之前的字符一样，也是可以match的，只需要看看这match的部分之前是否是match的即可，也就是去看
dp[i-1][j-2]
又因为当前为的情况 dp[i] [j] = dp[i] [j – 2]，可以dp[i-1][j]

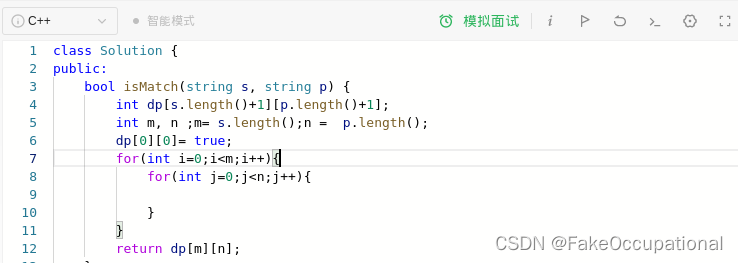
class Solution {
public:
    bool isMatch(string s, string p) {
        int dp[s.length()+1][p.length()+1];
        int m, n ;m= s.length();n =  p.length(); 
        //初始化
        memset(dp,0,sizeof(dp));//https://blog.csdn.net/weixin_44807751/article/details/103793473
        dp[0][0]= true;
        
        for(int j=1;j<n+1;j++){//对第一行的所有列进行初始化
            if (p[j-1] == '*')
                dp[0][j] = dp[0][j-2];
            else
                dp[0][j] = false;
        }

        // 继续填写
        for(int i=1;i<m+1;i++){
            for(int j=1;j<n+1;j++){
                if (p[j-1]=='.' || p[j-1]==s[i-1]){

                        dp[i][j] =dp[i-1][j-1];

                }else if(p[j-1]=='*' && j>=2){
                    if(p[j-2] == s[i-1] || p[j-1-1]=='.'){
                        dp[i][j] = dp[i-1][j] || dp[i][j-2];
                    }else{
                        dp[i][j] =  dp[i][j-2];
                    }
                }else{
                    dp[i][j] = false;
                }
            }
        }
        return dp[m][n];
    }
};

参考与更多

暴力匹配做法执行用时：0 ms, 在所有 C 提交中击败了100.00%的用户

bool isMatch(char * s, char * p)
{
    int slen = strlen(s);
    int plen = strlen(p);
    char c;
    int i,j;
    int ret;
    
    if(slen == 0 && plen != 0 && *(p + 1) != '*')
    {//如果s串已空而p串不可能空，不匹配
        return 0;
    }
    if(plen > 0 && *(p + 0) == '.')
    {//如果p串第一个字符是'.'
        if(plen > 1 && *(p + 1) == '*')
        {//如果p串第二个字符是'*'
            //跳过带'*'的字串，*(p + j)第一个不跟'*'的字符
            for(j = 2; j + 1 < plen && *(p + j + 1) == '*'; j += 2);

            if(plen == j)
            {//p串已经到了末尾
                return 1;
            }
            else
            {
                for(i = 0; i < slen; i ++)
                {//考虑到'.*'的特殊性只能挨个将字串与之尝试匹配
                    if(*(s + i) == *(p + j) || *(p + j) == '.')
                    {
                        if(isMatch(s + i, p + j))
                        {
                            return 1;
                        }
                    }
                }
                return 0;
            }
        }
        else//'.'匹配到任意字符
        {

            return isMatch(s + 1,  p + 1);
        }
    }
    else if(plen > 0)
    {
        //如果p串第一个字符是非'.'的字符
        if(plen > 1 && *(p + 1) == '*')
        {
            //如果p串第二个字符是'*'
            //跳过与p串首字符相等且带'*'的字串，*(p + j)第一个不跟'*'或不与p串首字符相等的字符
            for(j = 2; j + 1 < plen && *(p + j) == *(p + 0) && *(p + j + 1) == '*'; j += 2);
            //
            if(plen == j)
            {
                //p串已经到了末尾
                for(i = 0; i < slen && *(s + i) == *(p + 0); i ++);
                if(i == slen) 
                {
                    return 1;
                }
                else
                {
                    return 0;
                }
            }
            else
            {
                //考虑到带'*'的特殊性只能挨个将字串与之尝试匹配
                for(i = 0; i < slen && *(s + i) == *(p + 0); i ++)
                {
                    if(isMatch(s + i, p + j))
                    {
                        return 1;
                    }
                }
                return isMatch(s + i, p + j);
            }
        }
        else if(*s == *p)
        {//两个字串首字符相等匹配到任意字符
            return isMatch(s + 1,  p + 1);
        }
        else return 0;
    }
    //p串空后根据s串的剩余长度判断结果
    if(slen > 0)
    {
        return 0;
    }
    else
    {
        return 1;
    }
}

逆推法
状态归纳+边界条件

public static int uniquePaths(int m, int n) {
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[][] dp = new int[m][n]; // 
    // 初始化
    for(int i = 0; i < m; i++){
      dp[i][0] = 1;
    }
    for(int i = 0; i < n; i++){
      dp[0][i] = 1;
    }
        // 推导出 dp[m-1][n-1]
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    return dp[m-1][n-1];
}

视频图解动态规划正则表达式

用两个指针顺序读取是无法实现的，因为不知道*需要匹配几个（需依次比较，当某个不匹配时即为匹配的个数）。

添加链接描述

class Solution {
public:
    bool isMatch(string s, string p) {
        if (p.empty()) return s.empty();
        
        auto first_match = !s.empty() && (s[0] == p[0] || p[0] == '.');
        
        if (p.length() >= 2 && p[1] == '*') {
            return isMatch(s, p.substr(2)) || (first_match && isMatch(s.substr(1), p));
        } else {
            return first_match && isMatch(s.substr(1), p.substr(1));
        }
    }