Blind Backdoors in Deep Learning Models 论文笔记

news2025/2/27 1:59:44

#论文笔记#

1. 论文信息

论文名称	Blind Backdoors in Deep Learning Models
作者	Eugene Bagdasaryan Vitaly Shmatikov Cornell Tech
出版社	USENIX Security Symposium 2021 （网安A类会议）
pdf	论文主页本地PDF
代码	pytoch_Backdoors_101

2. introduction

2.1 背景

blind backdoor attack

文章提出了一种新的 backdoor attack 的方式。文中称为 blind backdoor attack

文中关于 blind backdoor attack 的解释如下：

Our attack is blind: the attacker cannot modify the training data, nor observe the execution of his code, nor access the resulting model

具体来说：攻击者知道主要任务，可能的模型架构和常用的数据。但是不知道具体的训练数据，参数和结果模型。由于上述限制，blind attack 比其他 backdoor attack 更加难做到。

backdoor attack 的分类

如何做到 blind backdoor attack ，以及 blind backdoor attack 和其他的攻击方法有什么区别。作者画了一张图来描述 attack 的类型。其中 blind backdoor attack 的方法属于 backdoor attack 中的 Code poisoning 的方法。即对开源代码库进行攻击。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Eq1sREsM-1669019216760)(assets/image-20220308154127-tsfbp11.png)]

上图总结了 5 中常见的代码攻击类型：

Poisoning：对训练数据进行投毒
Trojaning：对模型进行修改，注入后门（待了解）
model replacement：替换模型。联邦学习中的一种攻击方式（待了解）
Adversarial Example：对抗样本
Code poisoning：对代码进行投毒

关于 Code poisoning：

为什么可以进行代码攻击？

因为机器学习很多代码和开源框架都托管在Github等代码平台，这就导致了攻击者可以向开源代码中注入恶意代码，而且这些恶意代码比较难被审核者发现。文中的方法就是在代码中加入了一个后门学习的任务，导致使用者使用该代码训练模型会留下后门。

Code poisoning 和 data Poisoning 有什么区别？

Code poisoning 可以不用知道训练数据是什么。在 Data Poisoning 中，为了实现更好的效果往往需要根据数据的分布学习出一个带有目标类信息的 trigger 。所以 Data Poisoning 要预先得到训练数据，并在训练数据上构建模型，生成用于攻击的 poison data 。而 Code poisoning 不用考虑训练集的分布，只需要在 batch 中对数据集进行修改，即不管是什么样的训练集都可以用同一种方式攻击。

Data Poisoning 也有一定的局限性，在文章中提出，有一些数据是难以更改的（例如使用安全相机产生的数据）

2.2 文章的贡献

提出了 blind attack，并通过实验验证了 blind attack 的攻击效果
使用 multi-objective optimization 来看待 backdoor attack，并且使用了动态调整系数的方法
对防御方法进行分析，并验证了 blind attack 的有效性

3. method

3.1 模型结构图

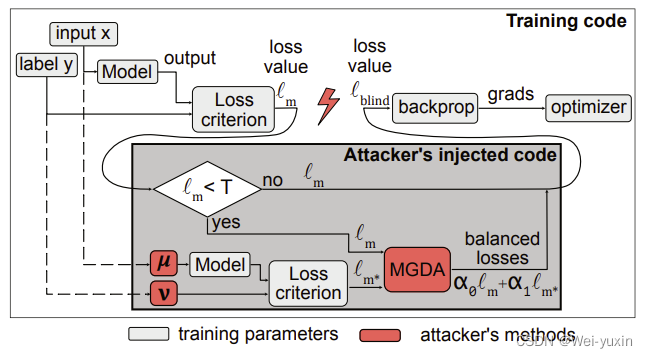
模型结构图
攻击过程

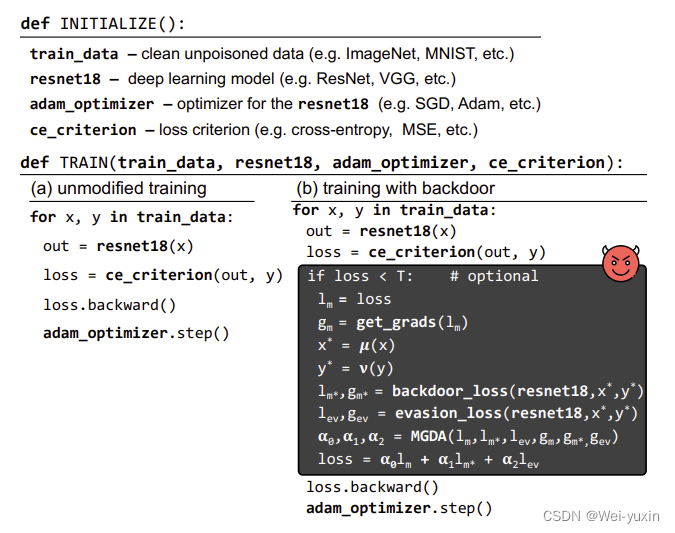
可以看到在攻击的过程中，攻击者只是在原本的代码中加入了几行新的代码。所以整个攻击比较隐秘且难以发现。攻击的方法可以理解为是多任务学习。

多任务学习

攻击使用的方法为多任务学习。多任务学习同时优化多个目标函数loss，学习出来的模型可以适应与不同任务。文章中将原本的分类任务视为主任务，将 backdoor attack 视为另一个任务。加入代码，让模型在学习主任务的同时，学习到次要任务。
- Main task：分类任务 $\ X ∗ , Y ) \theta^{*}(x)=y, \forall(x, y) \in\left(\mathcal{X} \backslash \mathcal{X}^{*}, \mathcal{Y}\right)$
- Backdoor task：将带有trigger的图片学习到目标类 $\ X ∗ , Y ) \theta^{*}(x)=y, \forall(x, y) \in\left(\mathcal{X} \backslash \mathcal{X}^{*}, \mathcal{Y}\right)$
训练的过程中，只增加了一个用于学习 backdoor 数据的 loss，并未改变优化器和模型结构
训练过程

开始仅训练主任务，在主任务 loss 小于一定阈值（接近收敛时），再开始训练多目标任务。这样的做法是为了减少开销，使得攻击过程更加隐蔽。

当然，从头直接训练多目标任务也是可行的。
损失函数
$\ell_{\text {blind }}=\alpha_{0} \ell_{m}+\alpha_{1} \ell_{m^{*}}\left[+\alpha_{2} \ell_{e v}\right]$
- main task loss：$ \ell_{m}$
- backdoor loss: $\ell_{m^{*}}$
- optional evasion loss： $\ell_{e v}$
  
  $\ell_{e v}$ 是为了对抗防御模型 Neural Cleanse 设计的损失
loss 间的系数

多任务学习中存在一个问题：不同任务 loss 之间的系数取决于数据和模型，使用固定的系数组合不是最优解。

文章中给出了一个解决方法，use Multiple Gradient Descent Algorithm with the Franke-Wolfe optimizer [16, 81] to find an optimal 。

使用 MGDA 算法，动态调整损失函数的权重

MGDA： $\min _{\alpha_{1}, \ldots, \alpha_{k}}\left\{\left\|\sum_{i=1}^{k} \alpha_{i} \nabla \ell_{i}\right\|_{2}^{2} \mid \sum_{i=1}^{k} \alpha_{i}=1, \alpha_{i} \geq 0 \forall i\right\}$
关于 $\mu$ 和 $v$

$v$ 可以设置为不同的 target label， $\mu$ 的数量也可以灵活变