7.4.分块查找

一.分块查找的算法思想：

1.实例：

以上述图片的顺序表为例，

该顺序表的数据元素从整体来看是乱序的，但如果把这些数据元素分成一块一块的小区间，

第一个区间[0,1]索引上的数据元素都是小于等于10的，

第二个区间[2,5]索引上的数据元素都是小于等于20的，

第三个区间[6,8]索引上的数据元素都是小于等于30的，

第四个区间[9,10]索引上的数据元素都是小于等于40的，

第五个区间[11,13]索引上的数据元素都是小于等于50的，以此类推，

因此该顺序表虽然整体看起来是乱序的，但是当我们把顺序表分成一块一块的小区间之后，会发现各个区间之间其实是有序的，

可以给这个顺序表(查找表)建立上一级的索引，如下图：

如上图，

"索引表"当中保存的是每一分块中最大的关键字，和对应的分块的存储区间，

比如"索引表"的2索引中保存了30和[6,8]，也就是说顺序表中第3个分块中出现的最大关键字是30，且该分块的存储区间是[6,8]，其他同理，

所以分块查找的特点是"块内无序、块间有序"，如果看每一个分块之间，通过"索引表"可知各个分块中存储的最大关键字是递增的，也可以是递减的，

如下图：

2."索引表"的代码实现：

#include<stdio.h>

//索引表
typedef struct
{
    int maxValue; //顺序表中每一分块的最大关键字，该关键字的数据类型不固定，但要与顺序表里的元素类型保持一致 
    int low,high; //low和high指的是当前所指的分块的区间范围[low,high] 
}Index; //索引表的类型 

//顺序表存储的实际元素
int List[100]; 

int main()
{
    return 0;
}

二.分块查找的演示：

1.例一：对索引表采取顺序查找来判断要查找的目标关键字所属的分块

如上图，

如果本次要查找的目标关键字是22，需要先查找"索引表"，从"索引表"的第一个元素依次往后找，

第一个元素是10即该分块内的元素都是小于等于10的，所以关键字22不可能在该分块内；

第二个元素是20即该分块内的元素都是小于等于20的，所以关键字22不可能在该分块内；

第三个元素是30即该分块内的元素都是小于等于30的，所以如果22存在于该顺序表中，那么只可能在该分块内，

因此接下来就从该分块的起始位置即数组的6索引的位置开始查找，

如下图：

如上图，顺序表里的6索引上的元素27不等于要查找的目标关键字22，

所以要往后找一个索引，因此接下来是7索引上的元素22，与要查找的目标关键字22相等，

至此，查找成功，

如下图：

2.例二：对索引表采取顺序查找来判断要查找的目标关键字所属的分块

如上图，

如果本次要查找的目标关键字是29，需要先查找"索引表"，从"索引表"的第一个元素依次往后找，

第一个元素是10即该分块内的元素都是小于等于10的，所以关键字29不可能在该分块内；

第二个元素是20即该分块内的元素都是小于等于20的，所以关键字29不可能在该分块内；

第三个元素是30即该分块内的元素都是小于等于30的，所以如果29存在于该顺序表中，那么只可能在该分块内，

因此接下来就从该分块的起始位置即数组的6索引的位置开始查找，

如下图：

如上图：

在第三个分块内即顺序表的6索引到8索引上，不存在要查找的目标关键字29，

再往后就指向了9索引上的元素，此时已经超出了第三个分块范围，说明查找失败，

如下图：

3.例三：对索引表采取折半查找来判断要查找的目标关键字所属的分块

如上图，

如果本次要查找的目标关键字是30，需要先查找"索引表"，

根据折半查找规则，初始需要通过索引表的开头即low指针指向的位置和索引表的末尾即high指针指向的位置来求出中间指针mid的位置，再尝试找到30这个关键字所属的分块，

初始时low为0，high为4，根据mid=(low+high)/2可知mid等于2，

所以mid初始指向的元素是索引表上2索引的元素30即该分块内的元素都是小于等于30的，所以如果30存在于该顺序表中，那么只可能在该分块内（因为要查找的目标关键字30等于该分块的最大元素30），

所以接下来会从该分块内即顺序表的6索引到8索引上依次往后查找，

如下图：

如上图，

在该分块内通过查找发现顺序表里8索引上的元素30等于要查找的目标关键字30，

至此，查找成功，

如下图：

4.例四：对索引表采取折半查找来判断要查找的目标关键字所属的分块

如上图，

如果本次要查找的目标关键字是19，显然19存在于顺序表中（注：不是索引表），但和例三不一样的是，例三中要查找的目标关键字30，这个要查找的目标关键字30可以直接在索引表中找到，但是现在要查找的目标关键字19并没有被直接包含在索引表中，

首先需要查找"索引表"，

根据折半查找规则，初始需要通过索引表的开头即low指针指向的位置和索引表的末尾即high指针指向的位置来求出中间指针mid的位置，再尝试找到19这个关键字所属的分块，

初始时low为0，high为4，根据mid=(low+high)/2可知mid等于2，

所以mid初始指向的元素是索引表上2索引的元素30即该分块内的元素都是小于等于30的，

但19是小于索引表中的30的，

根据分块查找的规则要把high指针指向mid-1的位置即high指针指向1索引，low指针不变，

（注：索引表是按照升序排列的）

如下图：

如上图，

此时low指针指向0索引上的元素即low为0，high指针指向1索引上的元素即high为1，

根据mid=(low+high)/2可知mid等于0，

所以mid指向的元素是索引表上0索引的元素10即该分块内的元素都是小于等于10的，

但19是大于索引表中的10的，

根据分块查找的规则要把low指针指向mid+1的位置即low指针指向1索引，high指针不变，

（注：索引表是按照升序排列的）

如下图：

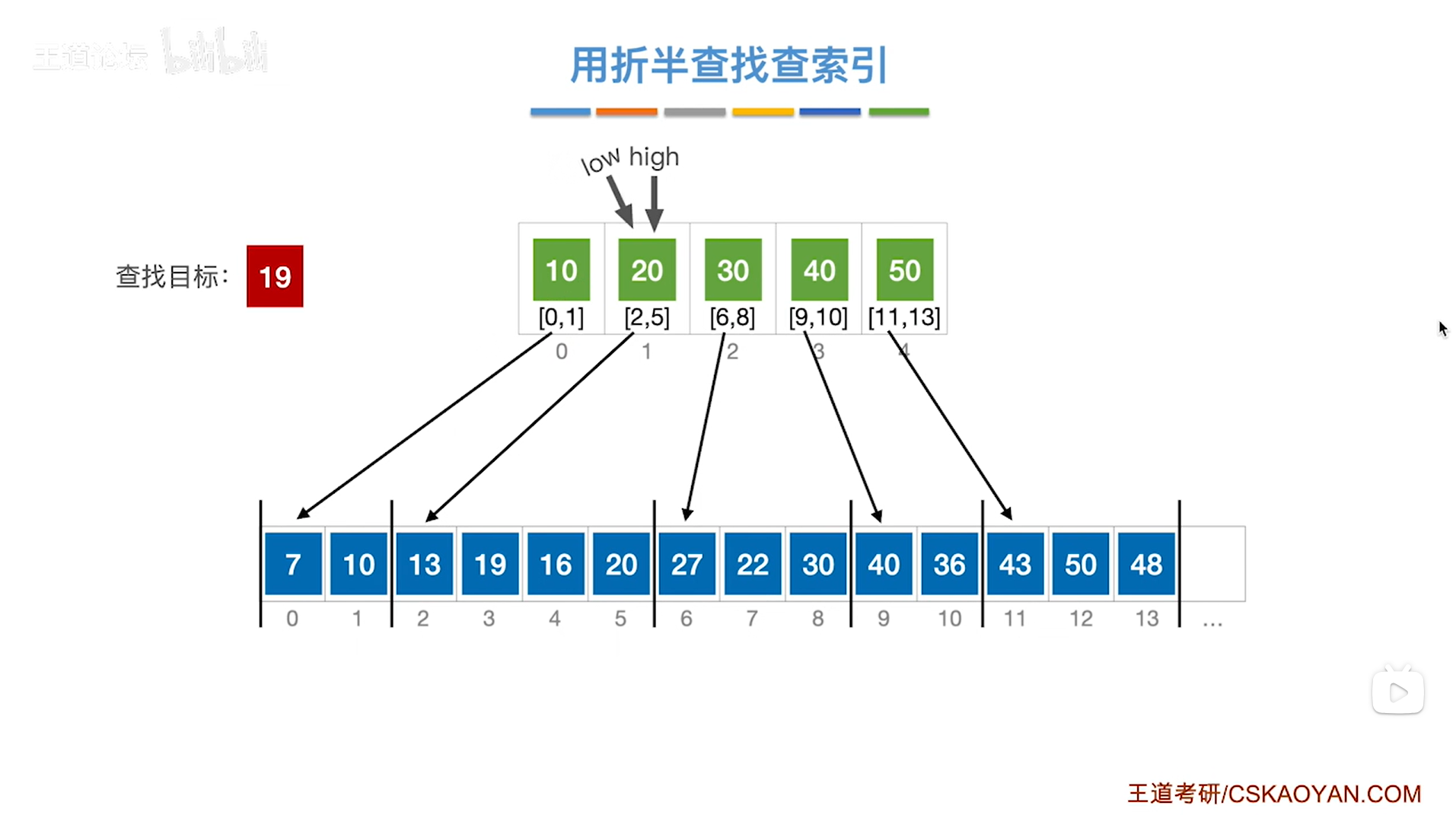
如上图，

此时low指针指向1索引上的元素即low为1，high指针指向1索引上的元素即high为1，

根据mid=(low+high)/2可知mid等于1，

所以mid指向的元素是索引表上1索引的元素20即该分块内的元素都是小于等于20的，

但19是小于索引表中的20的，

根据分块查找的规则要把high指针指向mid-1的位置即high指针指向0索引，low指针不变，

（注：索引表是按照升序排列的）

如下图：

如上图，

此时low指针指向1索引上的元素即low为1，high指针指向0索引上的元素即high为0，

会发现low>high，按照折半查找的规则，到这一步意味着折半查找失败，但实际上要查找的目标关键字19其实是在low指针指向的分块中，所以接下来应该在low指向的分块中进行查找，

如下图：

如上图，

类似本例，如果要查找的目标关键字并没有被直接地包含在索引表中，那么对索引表进行折半查找，最终会导致折半查找出现在low>high的情况，

每当发生这种情况的时候，需要在low指针所指的分块中进行下一步的查找，

具体原因如下：

折半查找失败最终的结果是low>high（详情见"7.3.折半查找(二分查找)"），但是在low>high之前的那一步肯定是low=high，所以当low=high时，mid、low、high三个指针指向的是同一个位置，此时可能发生两种情况：假设mid=low=high=a，且索引表中的元素是升序排序

第一种情况是中间指针mid所指的分块的最大值小于要查找的目标关键字key，这种情况会让low指针指向mid+1的位置即a+1，high指针不变即high为a，此时mid=(low+high)/2=(a+1+a)=a（C语言会取整），最终low所指的元素一定要比mid所指的元素更大
第二种情况是中间指针mid所指的分块的最大值大于要查找的目标关键字key，这种情况会让high指针指向mid-1的位置即a-1，low指针不变即low为a，此时mid=(low+high)/2=(a+a-1)/2=a（C语言会取整），最终low>high的时候，low指针所指向的位置a上的关键字一定会大于要查找的目标关键字（参考例四）
注：这种情况下中间指针mid所指的分块的最大值不会等于要查找的目标关键字key（因为题目要求）

再结合索引表的特性，索引表当中保存的是每一个分块中最大的关键字，所以要对索引表中比目标关键字大的那个分块进行查找才有可能找到目标关键字，

通过刚才的分析可知，无论发生哪种情况，当low>high即折半查找失败时，一定是low指针指向的那个分块的关键字比要查找的目标关键字更大，所以这就是为什么最终要查找low指针指向的分块，

如下图：

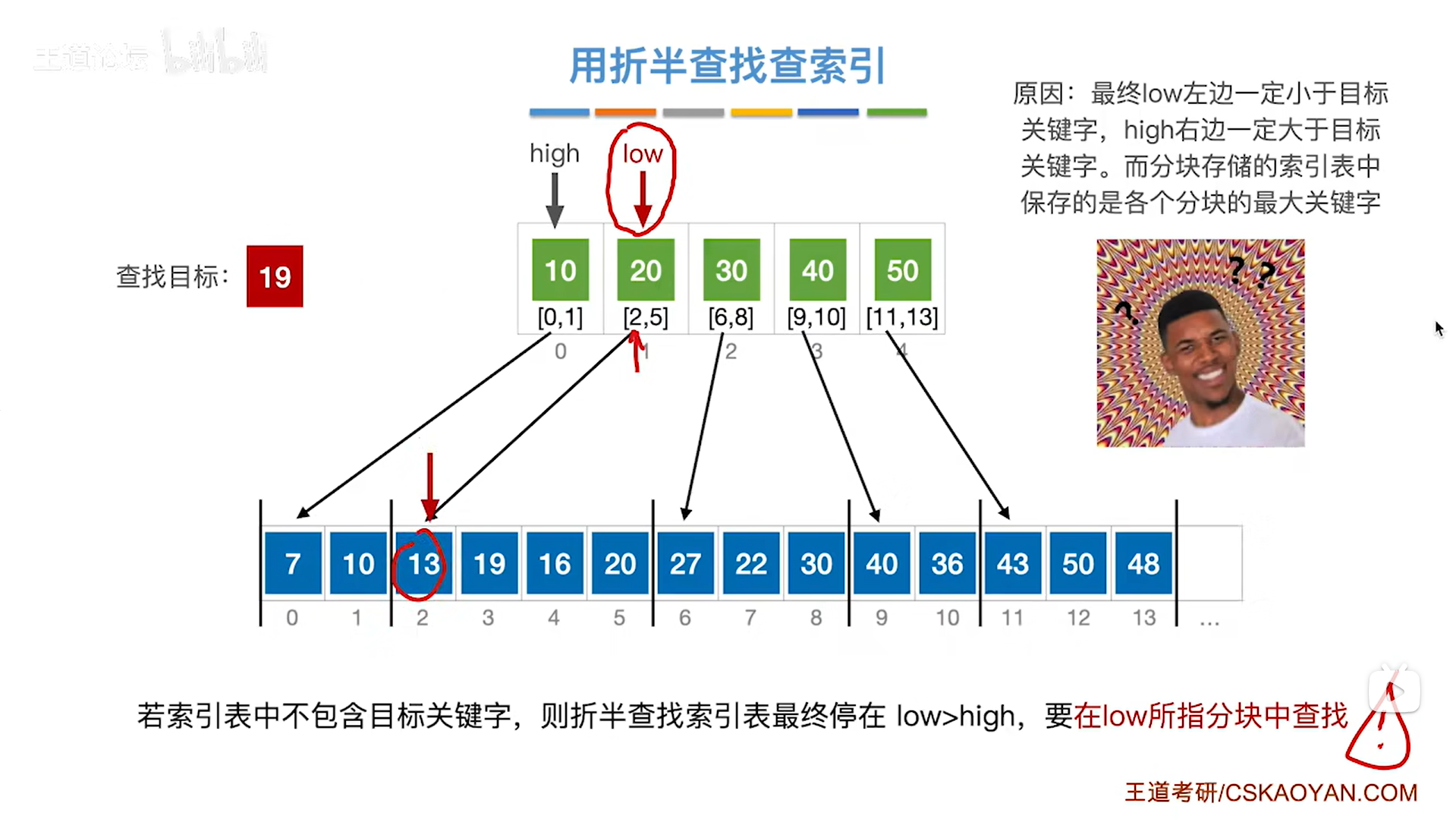
如上图：

继续例四，通过之前的分析可知，要在low指针指向的分块即顺序表中2索引到5索引的位置上进行顺序查找目标关键字，

首先顺序表里的2索引上的元素13不等于要查找的目标关键字19，

所以要往后找一个索引，因此接下来是3索引上的元素19，与要查找的目标关键19相等，

至此，查找成功，

如下图：

5.例五：对索引表采取折半查找来判断要查找的目标关键字所属的分块

如上图，

如果本次要查找的目标关键字是54，

首先需要查找"索引表"，

根据折半查找规则，初始需要通过索引表的开头即low指针指向的位置和索引表的末尾即high指针指向的位置来求出中间指针mid的位置，再尝试找到54这个关键字所属的分块，

初始时low为0，high为4，根据mid=(low+high)/2可知mid等于2，

所以mid初始指向的元素是索引表上2索引的元素30即该分块内的元素都是小于等于30的，

之后根据折半查找的规则（可参考例四），"索引表"最终的查找结果如下，

（注：索引表是按照升序排列的）

如下图：

如上图，

最终是high为4，low为5，同样是low>high，

由之前的分析可知，最终要在low所指的分块中进行查找，但是由于现在low所指的分块已经超出了索引表，

因此low指针为空，所以这种情况就意味着查找失败。

6.总结：

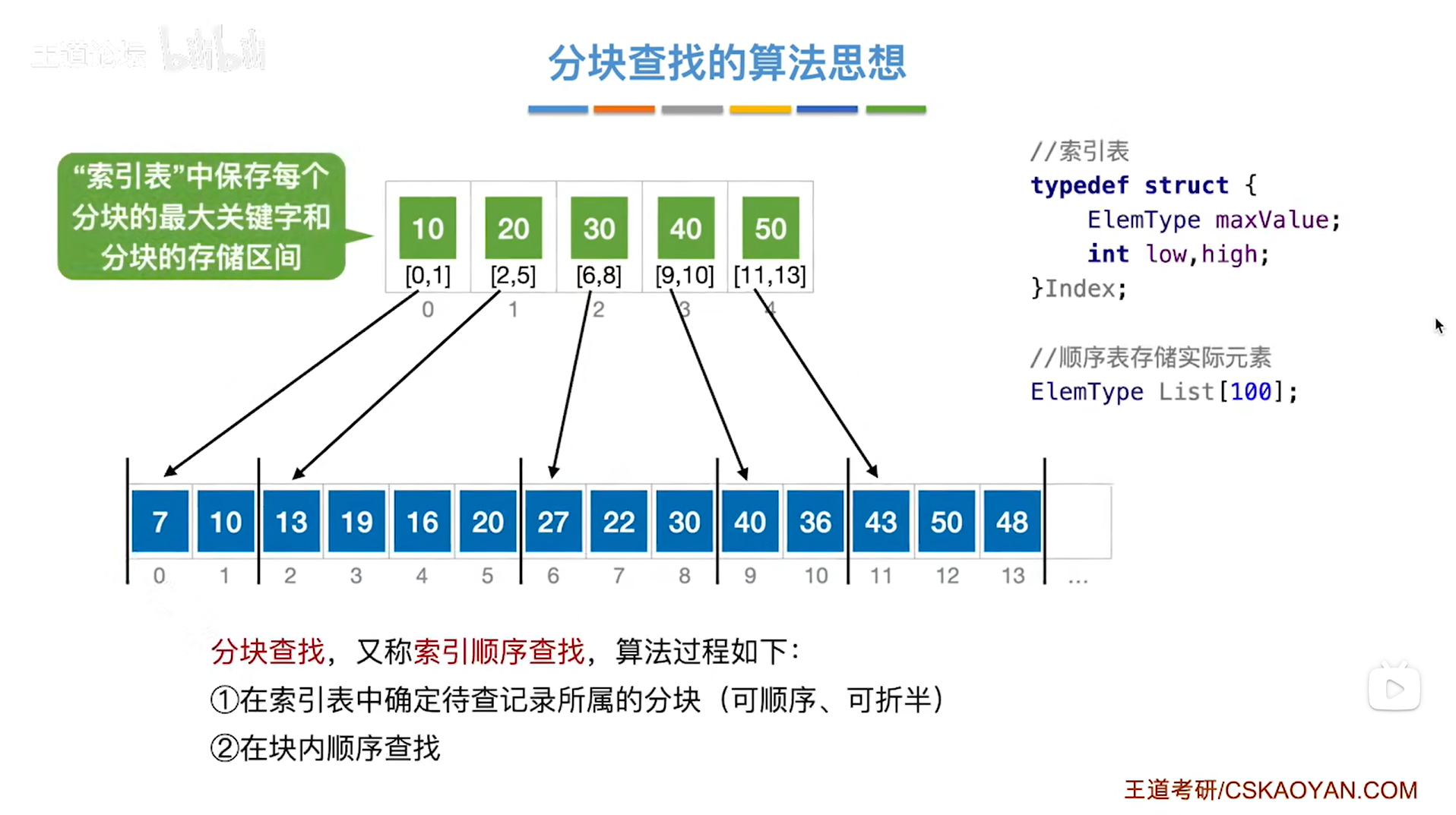
分块查找，又称索引顺序查找（因为刚开始查找的是索引表，然后是在顺序表中顺序查找索引表所指向的分块），算法过程如下：

步骤一：在索引表中确定待查记录所属的分块（注：判断待查记录在哪一个分块，可以通过顺序查找，也可以通过折半查找，因为索引表中保存的元素是有序的，并且索引表是用数组的形式即顺序存储来实现的，所以对索引表的查找也可以使用折半查找）

步骤二：在所属的分块内进行顺序查找（因为分块内的元素大多是乱序存放的，所以只能采取顺序查找来依次往后对比查找）

三.分块查找的查找效率分析（ASL）：

1."索引表"采用顺序查找的情况下（查找成功）：

以上述图片的顺序表为例，对应的"索引表"已给出，

顺序表中共有14个数据元素有可能被查找，假设每一个数据元素被查找的概率相等，那么每一个数据元素的查找概率Pi为1/14，

如果对"索引表"采取顺序查找的方式，

假设此时要查找的目标关键字为7，总共需要对比关键字的次数（查找长度）为2次：在"索引表"中对比到第一个关键字就可以确定7所属的分块（此时共对比了1次关键字），在对应的分块中顺序对比到第一个关键字就找到了最终目标7（此时共对比了2次关键字），所以总共需要对比2次关键字即C1为2->所以ASL中的第一项为P1 * C1 = 1/14 * 2；

假设此时要查找的目标关键字为10，总共需要对比关键字的次数（查找长度）为3次：在"索引表"中对比到第一个关键字就可以确定10所属的分块（此时共对比了1次关键字），在对应的分块中顺序对比到第二个关键字就找到了最终目标10（此时共对比了3次关键字），所以总共需要对比3次关键字即C2为3->所以ASL中的第二项为P2 * C2 = 1/14 * 3；

假设此时要查找的目标关键字为13，总共需要对比关键字的次数（查找长度）为3次：在"索引表"中对比到第二个关键字就可以确定13所属的分块（此时共对比了2次关键字），在对应的分块中顺序对比到第一个关键字就找到了最终目标13（此时共对比了3次关键字），所以总共需要对比3次关键字即C3为3->所以ASL中的第三项为P3 * C3 = 1/14 * 3；

之后以此类推，

总之给出特定的例子，就可以分别找出查找每一个关键字所需要对比关键字的次数Ci，再乘以对应的被查找的概率Pi，最后把所有关键字的Pi * Ci相加就可以得到查找成功下的ASL。

2."索引表"采用折半查找的情况下（查找成功）：

以上述图片的顺序表为例，对应的"索引表"已给出，

顺序表中共有14个数据元素有可能被查找，假设每一个数据元素被查找的概率相等，那么每一个数据元素的查找概率Pi为1/14，

如果对"索引表"采取折半查找的方式，

假设此时要查找的目标关键字为30，根据折半查找的规则可知"索引表"中第一个检查的表象就是2索引上的30即该分块内的元素小于等于30，刚好与要查找的目标关键字30相等，所以经过这1次对比就可以确定要查找的目标关键字30所在于该分块内（2索引上的分块），在该分块内继续需要进行3次关键字的对比即可找到目标关键字30，所以总共需要4次关键字的对比即Ci为4；

类似地，

假设此时要查找的目标关键字为27，根据折半查找的规则可知"索引表"中第一个检查的表象就是2索引上的30即该分块内的元素小于等于30，要查找的目标关键字27比30小，因此可以确定要在该分块内进行查找，所以经过这1次对比就可以确定要查找的目标关键字27所在于该分块内（2索引上的分块），在该分块内继续需要进行1次关键字的对比即可找到目标关键字27，所以总共需要2次关键字的对比即Ci为2，但实际上这是错误的，因为虽然27比30小，但27也比28、29等数要小，无法确定查找27一定就要在30这个分块内查找，如果有28、29等分块，也可能在这些分块内查找，正确的如下->

对于要查找的目标关键字27，根据折半查找的规则可知"索引表"中第一个检查的表象就是中间指针mid即2索引上的30即该分块内的元素小于等于30，第一次对比了30这个表象之后会发现，当前表象的值要比目标关键字27更大，所以要让尾指针即high指针指向中间指针mid-1的位置即1索引处，头指针即low指针不变即指向0索引处，所以折半查找的第一轮并不能确定27所属的分块，必须在折半查找执行到high<low即"索引表"中折半查找失败的情况下，最终是high指向1，low指向2的时候，才可以确定27也是在30所属的分块内，因此要找27的话，对比2次关键字是错误的，具体需要对比几次与之前同理（详情见本篇的"二.4.例四"）；

之后以此类推，

3.分块查找中对于查找失败的情况非常复杂，一般不考：

对于分块查找来说，查找失败的情况就很难划分了，

因为"索引表"会出现查找失败的情况，

在各个分块之间，每一个分块里的元素是乱序的，查找时必须采用顺序查找，要得出查找失败也是需要很高的时间复杂度，

所以查找失败的情况不像之前折半查找能够明确划分出由哪些区间导致查找失败，在分块查找中如果要分析查找失败的ASL，分析起来要比查找成功的情况复杂得多。

4.特殊情况1：用顺序查找查索引表

通常情况下分块查找中每一个分块中的数据元素的个数都不相等，因此只能各个分块分开计算，

但是如果各个分块中数据元素的个数是相等的，这种情况下要计算分块查找的ASL，只需要把查找索引表的ASL和查找对应分块内的ASL进行相加，就可以得到总的分块查找的ASL，

以上述图片为例，

假设有一个长度为n的查找表，即查找表中共有n个数据元素，

现在把查找表均匀地分为b块，每块都有s个数据元素，所以就有n = s * b，

如果采用顺序查找的方式查找"索引表"，由于总共有b个分块即"索引表"共有b个数据元素，那么查找"索引表"的ASL为Li = (1+2+...+b) * 1/b = (b+1)/2，计算详解如下：

"索引表"共有b个数据元素可能被查找，假设每一个数据元素被查找的概率相等，那么每一个数据元素被查找的概率Pi为1/b，由于对"索引表"采用顺序查找，那么"索引表"中查找第一个数据元素的话只需要对比1次关键字即C1为1，查找第二个数据元素的话只需要对比2次关键字即C2为2，以此类推，查找第b个数据元素的话只需要对比b次关键字即Cb为b，所以查找"索引表"的ASL为Li = 1/b * 1 + 1/b * 2 +...+ 1/b * b = (1+2+...+b) * 1/b = (b+1)/2

在确定分块之后，还需要在长度为s的分块内进行顺序查找，对应的ASL为Ls = (1+2+...+s) * 1/s = (s+1)/2，计算详解如下：

每一个分块中都有s个数据元素可能被查找，假设每一个数据元素被查找的概率相等，那么每一个数据元素被查找的概率Pi为1/s，由于分块内只能采用顺序查找，那么查找第一个数据元素的话只需要对比1次关键字即C1为1，查找第二个数据元素的话只需要对比2次关键字即C2为2，以此类推，查找第s个数据元素的话只需要对比s次关键字即Cs为s，所以查找分块内的ASL为Ls = 1/s * 1 + 1/s * 2 +...+ 1/s * s = (1+2+...+s) * 1/s = (s+1)/2

最终把查找索引表的ASL和查找对应分块内的ASL相加，就可以得到分块查找的一个完整的ASL，即ASL = (b+1)/2 + (s+1)/2，

由于查找表总共有n个数据元素，被均匀地分为b块，每块都有s个数据元素，因此n = s * b，所以b = n/s，把b = n/s带入ASL = (b+1)/2 + (s+1)/2即可得到ASL = (s * s + 2s + n)/2s，

ASL = (s * s + 2s + n)/2s = s/2 + 1 + n/2s，这就是分块查找在查找成功情况下的ASL。

现在要思考的问题是在什么情况下该ASL最小？其实就是求最值的问题，

根据均值不等式（也可以求导得出，注：n、s、b都是大于等于0的）

ASL = s/2 + 1 + n/2s >= 1+2√s/2 * n/2s = 1+√n，当且仅当s/2=n/2s即s=√n时取等，因此ASL的最小值为1+√n，

所以分块查找的ASL在把n个数据元素分为b块即b=n/s=n/√n=√n块，每一分块中有s即√n个数据元素时ASL最小，ASL的最小值为1+√n。

->比如n=10000即查找表中有10000个数据元素，那么最优的一种分块方案是把这10000个数据元素分成√10000=100块，然后每一块中有√10000=100个数据元素，这种情况下可以得到最小的ASL为1+√10000=1+100=101，意味着平均要对比101次关键字即可找到目标关键字。

相比于顺序查找来说，分块查找的效率提升了很多，如果有10000个数据元素，采用顺序查找的话ASL=1/10000 * 1 + 1/10000 * 2 + ... + 1/10000 * 10000 = (1+2+...+10000)/10000=50000.5，意味着平均要对比50000.5次才可以找到目标关键字，所以采用分块查找要比顺序查找高效得多。