算法打卡第18天

从中序与后序遍历序列构造二叉树

(力扣106题)

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

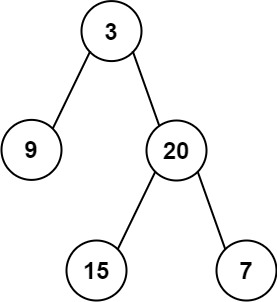
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由不同的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

解题思路

这道题的解题思路是利用二叉树的中序遍历和后序遍历结果来重建二叉树。中序遍历的特点是左根右，后序遍历的特点是左右根。通过这两个遍历结果，可以唯一确定一棵二叉树。

确定根节点：后序遍历的最后一个元素是当前子树的根节点。
切割中序遍历：在中序遍历中找到根节点的位置，其左侧是左子树的中序遍历，右侧是右子树的中序遍历。
切割后序遍历：根据左子树的中序遍历长度，从后序遍历中切分出左子树和右子树的后序遍历。
递归构建：对左子树和右子树分别递归执行上述步骤，直到所有子树都被构建完成。

通过递归的方式，利用中序和后序遍历的特性，可以高效地重建出原始的二叉树。

代码

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
    ~TreeNode()
    {
        delete left;
        delete right;
    }
};

class Solution
{
    // 递归地构建二叉树
    // 函数直接操作原始的vector对象，而不是创建一个副本
private:
    TreeNode *traversal(vector<int> &inorder, vector<int> &postorder)
    {
        // 空数组
        if (postorder.size() == 0)
        {
            return NULL;
        }
        // 后序遍历数组最后一个元素，就是当前的根节点
        int rootValue = postorder[postorder.size() - 1];
        // 构建根节点
        TreeNode *root = new TreeNode(rootValue);
        // 当前子树只有一个节点（即叶子节点）
        if (postorder.size() == 1)
        {
            return root;
        }
        // 找到中序遍历的切割点
        int delimiterIndex = 0;
        for (delimiterIndex; delimiterIndex < inorder.size(); delimiterIndex++)
        {
            if (inorder[delimiterIndex] == rootValue)
            {
                break;
            }
        }
        // 切中序数组
        // 左闭右开区间：[0, delimiterIndex)
        // 是C++标准库中对范围的约定是左闭右开
        vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
        // [delimiterIndex + 1, end)
        vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end());
        // postorder 舍弃末尾元素，因为这个元素就是中间节点，已经用过了
        // resize调整数组大小
        postorder.resize(postorder.size() - 1);
        // 左闭右开，注意这里使用了左中序数组大小作为切割点：[0, leftInorder.size)
        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        vector<int> rightPostorder(postorder.begin() + leftInorder.size() , postorder.end());

        cout << "----------" << endl;
        cout << "leftInorder :";
        for (int i : leftInorder)
        {
            cout << i << "";
        }
        cout << endl;
        cout << "rightInorder :";
        for (int i : rightPostorder)
        {
            cout << i << "";
        }
        cout << endl;

        cout << "leftPostorder :";
        for (int i : leftPostorder)
        {
            cout << i << "";
        }
        cout << endl;

        cout << "rightPostorder :";
        for (int i : rightPostorder)
        {
            cout << i << "";
        }
        cout << endl;

        // 递归
        root->left = traversal(leftInorder, leftPostorder);
        root->right = traversal(rightInorder, rightPostorder);
        return root;
    }

public:
    TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder)
    {
        if (inorder.size() == 0 || postorder.size() == 0)
        {
            return NULL;
        }
        return traversal(inorder, postorder);
    }
};
// 打印函数
void printTree(TreeNode *root)
{
    if (root == nullptr)
    {
        return;
    }
    queue<TreeNode *> que;
    que.push(root);
    while (!que.empty())
    {
        TreeNode *current = que.front(); // 取出队列中的当前节点
        que.pop();                       // 从队列中移除当前节点
        // 打印当前节点的值
        cout << current->val << "";
        // 如果当前节点有左子节点，将左子节点加入队列
        if (current->left)
        {
            que.push(current->left);
        }
        if (current->right)
        {
            que.push(current->right);
        }
    }
}

最大二叉树

(力扣654题)

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 *最大二叉树* 。

示例 1：

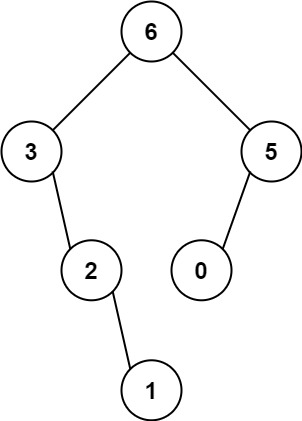
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

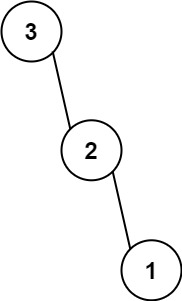
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

解题思路

这道题的解题思路是利用递归构建最大二叉树。最大二叉树的定义是：对于每个节点，其左子树上的所有值都小于该节点的值，右子树上的所有值都大于该节点的值。

递归终止条件：如果输入数组的大小为1，则直接创建一个值为该元素的节点并返回，因为此时已经到达叶子节点。
寻找最大值及其索引：遍历数组，找到最大值及其索引。最大值将作为当前子树的根节点。
构建根节点：根据最大值创建根节点。
递归构建左右子树：
- 左子树：最大值左侧的数组元素用于构建左子树。如果最大值索引大于0，则递归调用函数构建左子树。
- 右子树：最大值右侧的数组元素用于构建右子树。如果最大值索引小于数组长度减1，则递归调用函数构建右子树。
返回根节点：递归完成后，返回构建好的根节点。

通过递归的方式，每次选择数组中的最大值作为当前子树的根节点，并分别用其左侧和右侧的数组元素构建左右子树，最终构建出满足条件的最大二叉树。

代码

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// 最大二叉树
struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
    ~TreeNode()
    {
        delete left;
        delete right;
    }
};

class Solution
{
public:
    TreeNode *constructMaximumBinaryTree(vector<int> &nums)
    {
        // 确定终止条件 果传入的数组大小为1，说明遍历到了叶子节点了
        TreeNode *node = new TreeNode(0);
        if (nums.size() == 1)
        {
            node->val = nums[0];
            return node;
        }
        // 找到数组中最大的值和对应的下标 构建根节点

        int maxValue = 0; // 数组中最大的值
        int maxIndex = 0; // 数组中最大的值索引
        for (int i = 0; i < nums.size(); i++)
        {
            if (nums[i] > maxValue)
            {
                maxValue = nums[i];
                maxIndex = i;
            }
        }
        node->val = maxValue;
        // 上面的是创建根节点的逻辑
        //  最大值所在的下标左区间 构造左子树
        if (maxIndex > 0)
        {
            vector<int> newVec(nums.begin(), nums.begin() + maxIndex);
            node->left = constructMaximumBinaryTree(newVec);
        }
        // 最大值所在的下标右区间 构造右子树
        if (maxIndex <  nums.size() - 1)
        {
            vector<int> newVec(nums.begin() + maxIndex + 1, nums.end());
            node->right = constructMaximumBinaryTree(newVec);
        }
        return node;
    }
};
// 打印函数
void printTree(TreeNode *root)
{
    if (root == nullptr)
    {
        return;
    }
    queue<TreeNode *> que;
    que.push(root);
    while (!que.empty())
    {
        TreeNode *current = que.front(); // 取出队列中的当前节点
        que.pop();                       // 从队列中移除当前节点
        // 打印当前节点的值
        cout << current->val << "";
        // 如果当前节点有左子节点，将左子节点加入队列
        if (current->left)
        {
            que.push(current->left);
        }
        if (current->right)
        {
            que.push(current->right);
        }
    }
}
int main()
{
    TreeNode *root = new TreeNode(3);
    root->left = new TreeNode(9);
    root->right = new TreeNode(20);
    root->right->left = new TreeNode(15);
    root->right->right = new TreeNode(7);
    vector<int> inorder = {9, 3, 15, 20, 7};
    vector<int> postorder = {9, 15, 7, 20, 3};
    Solution s;

    return 0;
}

合并二叉树

(力扣617题)

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

两棵树中的节点数目在范围 [0, 2000] 内
-104 <= Node.val <= 104

解题思路

这道题的解题思路是通过递归合并两棵二叉树。合并规则是：对于两个树的每个对应节点，将它们的值相加，并将结果存储在一个新的节点中。如果某个节点在其中一棵树中不存在，则直接使用另一棵树中的节点。

递归终止条件：
- 如果 root1 为空，则直接返回 root2，因为 root2 就是合并后的结果。
- 如果 root2 为空，则直接返回 root1，因为 root1 就是合并后的结果。
合并节点：
- 如果两个节点都不为空，将它们的值相加，并存储在 root1 中（也可以选择存储在 root2 中，但这里选择 root1 作为主树）。
递归合并左右子树：
- 递归地合并左子树：root1->left = mergeTrees(root1->left, root2->left)。
- 递归地合并右子树：root1->right = mergeTrees(root1->right, root2->right)。
返回合并后的树：
- 最终返回 root1，它已经包含了合并后的所有节点。

通过递归的方式，逐层合并两棵树的节点，最终得到一棵新的二叉树，其中每个节点的值是两棵树对应节点值的和。这种方法既简洁又高效，充分利用了二叉树的递归结构。

代码

#include <iostream>
// 合并二叉树
struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
    ~TreeNode()
    {
        delete left;
        delete right;
    }
};
// 合并二叉树
class Solution
{
public:
    TreeNode *mergeTrees(TreeNode *root1, TreeNode *root2)
    {
        // 终止条件
        // 如果t1为空，合并之后就应该是t2
        if (root1 == NULL)
        {
            return root2;
        }
        // 如果t2为空，合并之后就应该是t1
        if (root2 == NULL)
        {
            return root1;
        }
        // 单层递归 节点都不是空
        // 修改了t1的数值和结构
        root1->val += root2->val;   //根
        root1->left = mergeTrees(root1->left, root2->left);    //左
        root1->right = mergeTrees(root1->right, root2->right);  //右
        return root1;
    }
};