短视频时长预估算法调研

weighted LR

$\frac{Tp}{1-p} \newline (1-p)odds = Tp \newline (Tp + odds * p) = odds \newline p = \frac{odds}{T + odds} \newline$

odds表示表示一个事件发生于不发生的比值，事件发生的几率
这里先对正样本进行加权，所以称作weighted LR
我们假设对 $l o g (o dd s)$ 进行参数化建模，其实也就是模型的logits，正常 $p$ 就是对logits进行sigmoid得到最后的点击率预估值，则有如下公式：

$log(\frac{Tp}{1-p}) = Wx + b \newline \frac{Tp}{1-p} = e^{Wx + b} \newline Tp = e^{Wx + b}(1 - p)$

因为 $p$ 很小，所以有

$\approx e^{Wx+b}$
5. 也就是时长预估等于对最后的logits取exp

D2Q

D2Q根据视频时长将视频划分为不同的组，在组内利用传统的回归模型进行预测，来减轻时长本身的偏差。
时长的顺序关系和条件依赖问题没有解决。

树回归

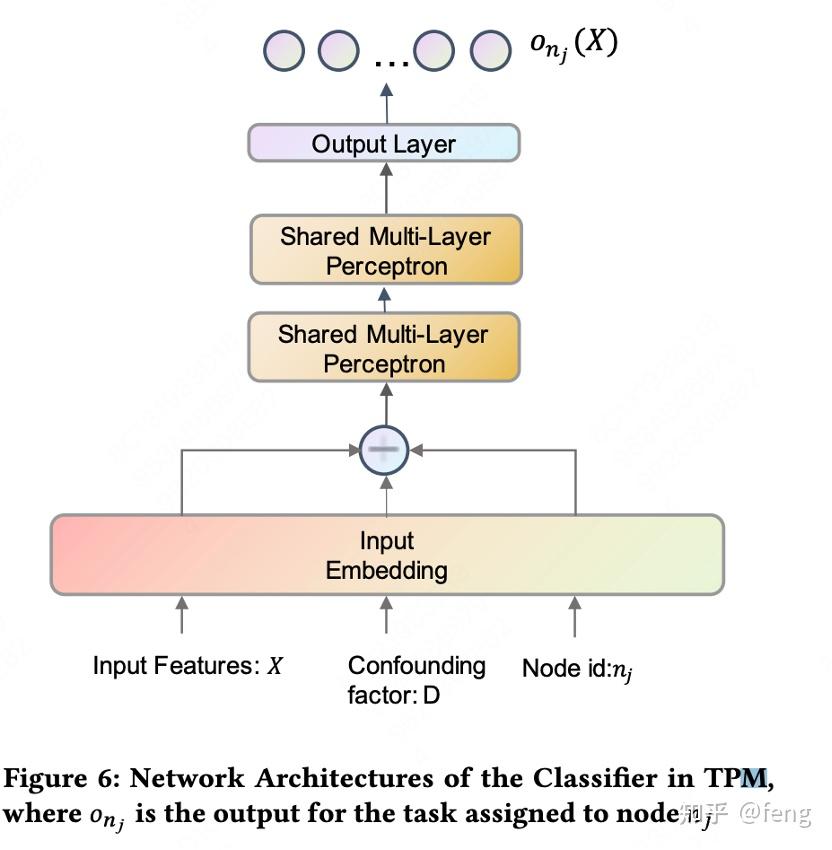
构建二叉树对时长进行分段，每个非叶子结点都是一个二分类器。2）文章的loss里面包含了分段预估的方差loss，这个方差其实就是在利用分段的顺序性

CREAD

整体的模型结构是比较基础的，就是一般的序列建模+分类预测。
在这里插入图片描述

Discretization

$\text{离散化:}\text{该模块是一个独立于训练和评估过程的预处理模块。它根据数据分布获得阈值集合} \ \{t_{m}\}_{m=1}^{M-1}, \\ \text{并将目标域} \ \mathcal{Y} \ \text{划分为} \ M \ \text{个互不重叠的区间} \ D \triangleq \{d_{m}=[t_{m-1}, t_{m})\}_{m=1}^{M}. \\ \text{这些区间用于将观看时长} \ y \ \text{转换为} \ m \ \text{个离散化的标签。}$ $y_m = \textbf1(y > t_m)$

Classification

$\ \text{个分类器被训练用于预测观看时长} \ y \ \text{是否大于第} \ m \ \text{个阈值} \ t_{m}, \ \text{即公式（1）中的} \ y_{m}, \ \text{并输出一系列概率：}$ $\hat{\phi}_m(\boldsymbol{x}_i; \Theta_m) = P(y > t_m | \boldsymbol{x}_i), \quad 1 \leq i \leq N.$

Restoration

$\text{给定} \ \{\hat{\phi}_m\}_{m=1}^M, \ \text{我们能够恢复预测的观看时长。恢复过程基于期望值的以下事实：}$ $\begin{aligned} \mathbb{E}(y|\boldsymbol{x}_i) &= \int_{t=0}^{t_M} t P(y = t|\boldsymbol{x}_i) dt \\ &= \int_{t=0}^{t_M} P(y > t|\boldsymbol{x}_i) dt \\ &\approx \sum_{m=1}^M P(y > t_m|\boldsymbol{x}_i) (t_m - t_{m-1}). \end{aligned}$

从第一步到第二步有一些跳跃，但是是等价的，我这里也推导出来:

期望值的积分表达式
题目中的第一个公式为：

$\mathbb{E}(y|\boldsymbol{x}_i) = \int_{0}^{t_M} t P(y = t|\boldsymbol{x}_i) dt,$

其中 $t|\boldsymbol{x}_i)$ 表示条件概率密度函数（若 $y$ 是连续型变量）。

生存函数的积分形式
对于非负随机变量 ( y )，其期望值可以表示为生存函数的积分：

$\mathbb{E}(y|\boldsymbol{x}_i) = \int_{0}^{t_M} P(y > t|\boldsymbol{x}_i) dt.$

这一转换的依据是

$\int_{0}^{t_M} P(y > t|\boldsymbol{x}_i) dt = \int_{0}^{t_M} \left( \int_{t}^{t_M} P(y = s|\boldsymbol{x}_i) ds \right) dt.$

通过交换积分顺序（Fubini定理），变为：

$\int_{0}^{t_M} \left( \int_{0}^{s} dt \right) P(y = s|\boldsymbol{x}_i) ds = \int_{0}^{t_M} s P(y = s|\boldsymbol{x}_i) ds,$

这正是原期望的表达式。因此，两式等价。

于是最终我们有：

$\hat{y} = \sum_{m=1}^{M} \hat{\phi}_m (t_m - t_{m-1}).$

EMD

在这里插入图片描述

这篇论文其实是用来解决存在类别间依赖的分类问题，可以很方便的替换掉传统交叉熵，而且可以和Distill softmax进行配合使用。

EMD距离

$\text{EMD被定义为将一个分布（直方图）的质量运输到另一个分布的最小成本。} \\ \\ \text{质量运输定义了从一组供应商簇向一组消费者簇运输质量的问题。其正式定义为：} \\ \text{设} \ \mathbf{p} = \{(\mathbf{a}_1, p_1), (\mathbf{a}_2, p_2), \ldots, (\mathbf{a}_C, p_C)\} \ \text{为供应商签名（分布或直方图），包含} \ C \ \text{个簇（箱），其中} \\ \mathbf{a}_i \ \text{表示每个簇，} \ p_i \ \text{表示每个簇中的质量（值）。} \text{设} \ \mathbf{t} = \{(\mathbf{b}_1, t_1), (\mathbf{b}_2, t_2), \ldots, (\mathbf{b}_{C'}, t_{C'})\} \ \text{为消费者签名。} \\ \text{设} \ \mathbf{D} \ \text{为基距离矩阵，其中其} \ i, j \ \text{项} \ \mathbf{D}_{i,j} \ \text{表示} \ \mathbf{a}_i \ \text{和} \ \mathbf{b}_j \ \text{之间的距离。矩阵} \ \mathbf{D} \ \text{通常定义为簇之间的l范数距离：} \\ \mathbf{D}_{i,j} = ||\mathbf{a}_i - \mathbf{b}_j||_l \quad (2)$ $\text{设} \ \mathbf{F} \ \text{为运输矩阵，其中其} \ i, j \ \text{项} \ \mathbf{F}_{i,j} \ \text{表示从} \ \mathbf{a}_i \ \text{运输到} \ \mathbf{b}_j \ \text{的质量。有效的运输需满足以下四个约束条件：}\\ \text{第一，运输的质量必须为正：} \\ \mathbf{F}_{i,j} \geq 0 \quad \text{对所有} \ i, j. \quad (3) \\ \text{第二，从供应商簇} \ p_i \ \text{运输的质量不得超过其总质量：} \\ \sum_{j=1}^{C'} \mathbf{F}_{i,j} \leq \mathbf{p}_i \quad \text{对所有} \ i. \quad (4) \\ \text{第三，运输到消费者簇} \ t_j \ \text{的质量不得超过其总质量：} \\ \sum_{i=1}^{C} \mathbf{F}_{i,j} \leq \mathbf{t}_j \quad \text{对所有} \ j. \quad (5)\\ \text{第四，总流量不得超过可运输的总质量：} \\ \sum_{i=1}^{C} \sum_{j=1}^{C'} \mathbf{F}_{i,j} = \min\left( \sum_{i=1}^{C} \mathbf{p}_i, \sum_{j=1}^{C'} \mathbf{t}_i \right). \quad (6)\\ \text{在上述约束条件下，定义流量} \ \mathbf{F} \ \text{的总成本为：}\\ W(\mathbf{b}, \mathbf{t}, \mathbf{F}) = \sum_{i=1}^{C} \sum_{j=1}^{C'} \mathbf{D}_{i,j} \mathbf{F}_{i,j}. \quad (7) \\ \text{EMD是两个向量之间的距离，记作EMD(p,t)，即满足约束条件（方程3、4、5、6）的最小工作成本，通过总流量归一化。} \\ \mathbf{EMD(p,t)=\inf _{\mathbf{F}}\frac{\sum\limits_{i=1}^{C}\sum\limits_{j=1}^{C'}\mathbf{D}_{i,j}\mathbf{F}_{i,j}}{\sum\limits_{i=1}^{C}\sum\limits_{j=1}^{C'}\mathbf{F}_{i,j}}} .$

顺序分类的基距离矩阵

$t_i$ 和 $t_j$ 的基距离矩阵是 $\|i-j\|$

EMD^2顺序矩分类损失

$\text{EMD被证明等价于Mallows距离，后者具有闭式解[23]，前提是基距离矩阵} \ \mathbf{D} \ \text{和分布} \ \mathbf{p} \ \text{和} \ \mathbf{t} \ \text{满足一定条件，如[23]所示。 \\ 们将展示这些条件在有序分类问题中得以满足。} \\ \\ \text{第一个条件是待比较的两个分布} \ \mathbf{p} \ \text{和} \ \mathbf{t} \ \text{必须具有相等的质量：} \ \sum_i p_i = \sum_j t_j. \\ \text{若} \ \mathbf{p} \ \text{由softmax层产生，则该条件恒成立，因为softmax层的输出向量是总和为1的归一化概率密度函数。由于预测分布的类别数与目标分布相同，故} \ C = C'. \\ \\ \text{第二个条件是基距离矩阵} \ \mathbf{D} \ \text{必须具有一维嵌入。假设在不失一般性的前提下，} \ p_1, p_2, \ldots, p_C \ \text{和} \ t_1, t_2, \ldots, t_{C'} \ \text{按其固有等级值排序，则该条件可表示为} \ \mathbf{D}_{i,j} = S(j - i), \\ \text{其中} \ S \ \text{为常数，且对所有满足} \ i \leq j \ \text{的} \ i, j \ \text{成立。显然，在有序分类问题中该假设总能满足。} \\ \\ \text{第三个也是最后一个条件是待比较的分布必须是排序后的向量。由于我们假设} \ p_1, p_2, \ldots, p_C \ \text{和} \ t_1, t_2, \ldots, t_{C'} \ \text{已排序，故该条件也总能满足。基于Levina等人的结论[23]，归一化EMD可精确且以闭式计算：} \\ \mathbf{EMD(\mathbf{p}, \mathbf{t}) = \left( \frac{1}{C} \right)^{\frac{1}{l}} ||\text{CDF}(\mathbf{p}) - \text{CDF}(\mathbf{t})||_l}, \\ \text{其中} \ \text{CDF}(\cdot) \ \text{是返回输入累积密度函数的函数。}$

这里是用的平方损失，可以将损失替换为交叉熵，参照推荐系统时长建模的常用方案 - Blog，可以得到和上一个方案的近似工程实现，不再赘述

Distill softmax

Distill Softmax是一种用于推荐系统时长建模的方法，它通过生成平滑的多分类软标签来考虑类别之间的关系。具体来说，Distill Softmax将时长信息转换为平滑的概率分布，而不是传统的独热编码（one-hot encoding）。以下是Distill Softmax的主要步骤：

时长分区间：将时长分成多个区间，例如10个区间。
生成平滑标签：对于真实时长所在的区间，生成一个平滑的概率分布。例如，如果真实时长在第5个区间，传统的多分类标签是[0,0,0,0,1,0,0,0,0,0]，而Distill Softmax会生成一个平滑的分布，如[0.001,0.005,0.03,0.1,0.7,0.1,0.05,0.008,0.005,0.001]。这样，相邻区间的概率会逐渐降低，从而更好地反映时长的连续性。
损失函数：使用多分类交叉熵作为损失函数，训练模型以预测这些平滑的概率分布。
线上预估：在实际应用中，通过累积概率分布来还原预测的时长。

Distill Softmax的优点在于它能够更好地利用类别之间的语义关系，提高模型的预测精度。它可以与其他方法（如EMD）结合使用，进一步提升效果。

总结来说，Distill Softmax通过生成平滑的软标签，使得模型在训练时能够更好地捕捉时长的连续性和类别之间的关系，从而提高预测的准确性。