决策树基础
回归树
理论上,决策区域可以有任何形状。•
然而,我们选择将预测空间划分为高维矩形或框,这是为了简单和易于解释结果预测模型
- 目标:将预测空间划分为矩形区域,最小化残差平方和(RSS)
∑ j = 1 J ∑ i ∈ R j ( y i − y ^ R j ) 2 \sum_{j=1}^J \sum_{i \in R_j} (y_i - \hat{y}_{R_j})^2 ∑j=1J∑i∈Rj(yi−y^Rj)2- y ^ R j \hat{y}_{R_j} y^Rj 为区域 R j R_j Rj 内样本响应的均值
- 示例(棒球运动员薪资预测):
- 关键分裂规则:
- R 1 = { X ∣ Years < 4.5 } R_1 = \{X \mid \text{Years} < 4.5\} R1={X∣Years<4.5}
- R 2 = { X ∣ Years ≥ 4.5 , Hits < 117.5 } R_2 = \{X \mid \text{Years} \geq 4.5, \text{Hits} < 117.5\} R2={X∣Years≥4.5,Hits<117.5}
- R 3 = { X ∣ Years ≥ 4.5 , Hits ≥ 117.5 } R_3 = \{X \mid \text{Years} \geq 4.5, \text{Hits} \geq 117.5\} R3={X∣Years≥4.5,Hits≥117.5}
- 区域𝑅1、𝑅2和𝑅3称为终端节点。
- 决策树通常是上下颠倒的,因为叶子在树的底部。
- 沿着预测空间被分割的树的点被称为内部节点。
- 结论:经验年限(Years)是薪资决定性因素,高经验球员中安打数(Hits)显著影响薪资
- 分类之后节点里的数据做平均作为预测值,分类任务则取众数
- 关键分裂规则:
分类树
-
预测方式:将样本划分至终端节点,预测该节点内最频繁的类别
最上面的节点是最重要的,对比线性模型,我们看P值,< 0.05说明重要
-
分裂标准:
-
基尼指数(衡量节点纯度):
Gini指数是衡量分类节点纯度的重要指标。
-
Gini指数衡量了所有 K K K个类别的总方差。
- 当所有 p ^ m k \hat{p}_{mk} p^mk(第 m m m个节点第 k k k类的比例)值都接近0或1时,Gini指数取较小值。
- 这种情况意味着节点中某个类别占多数,节点较纯。
-
因此,Gini指数被用来衡量节点的纯度(purity)。
- 较小的Gini值表明该节点中的观测值主要来自同一个类别。
总结来说,Gini指数越低,节点纯度越高,分类效果越好。
G = ∑ k = 1 K p ^ m k ( 1 − p ^ m k ) G = \sum_{k=1}^{K} \hat{p}_{mk}(1 - \hat{p}_{mk}) G=∑k=1Kp^mk(1−p^mk)
- p ^ m k \hat{p}_{mk} p^mk:区域 m m m 中第 k k k 类样本比例
- 值越小表示节点纯度越高
-
-
熵(替代指标):
D = − ∑ j = 1 J ∑ k = 1 K p j k log p j k D = -\sum_{j=1}^{J} \sum_{k=1}^{K} p_{jk} \log p_{jk} D=−∑j=1J∑k=1Kpjklogpjk
熵(Entropy)和基尼指数(Gini Index)都是衡量分类树中节点纯度的指标,但它们有以下区别:
-
定义不同
-
基尼指数:
G = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 G = \sum_{k=1}^K p_{k}(1 - p_{k}) = 1 - \sum_{k=1}^K p_k^2 G=k=1∑Kpk(1−pk)=1−k=1∑Kpk2
衡量节点中类别的不纯度,值越小越纯。 -
熵:
D = − ∑ k = 1 K p k log p k D = -\sum_{k=1}^K p_k \log p_k D=−k=1∑Kpklogpk
衡量信息的不确定性,值越小越纯。
-
-
数值范围和敏感性
- 基尼指数最大值通常是0.5(对于二分类,类别均匀分布时),对极端概率值敏感度较低。
- 熵最大值为 log K \log K logK,对概率分布更敏感,尤其是概率接近0或1时变化更剧烈。
-
计算复杂度
- 基尼指数计算相对简单,速度更快。
- 熵涉及对数运算,计算略复杂。
-
算法应用
- CART决策树常用基尼指数作为分裂标准。
- ID3和C4.5决策树常用熵和信息增益。
-
表现差异
在实际应用中,基尼指数和熵通常效果相近,差异不大,选择更多基于算法设计和偏好。
总结:
基尼指数和熵都是衡量节点纯度的指标,基尼指数偏重简单和计算效率,熵则有更强的信息理论基础和敏感度。 -

树的构建与剪枝
我们希望将特征空间划分为𝐽不同的区域。
但是尝试每一个可能的分区在计算上是不可行的。
相反,我们使用自上而下的贪婪方法(递归二进制分割):在每一步上,选择最佳的分割。在产生的子空间上递归地重复这个过程。
-
递归二叉分裂:
-
流程:从根节点(全体数据)开始,贪心地选择能最大程度降低RSS(回归)或提升纯度(分类)的分裂点
-
缺陷:局部最优且易过拟合
通过递归二叉分割生长的树可以产生深度、复杂的树,可以完美地拟合训练数据。这样的树可能会过拟合,因为它捕获的是噪声而不是信号
这导致高方差和较差的泛化
-
-
剪枝(控制复杂度):
- 代价复杂度剪枝 Cost-Complexity Pruning (the weakest link pruning):
$ C_{\alpha}(T) = \text{RSS} + \alpha |T| $- α \alpha α:权衡模型复杂度与拟合度的调参参数
- ∣ T ∣ |T| ∣T∣:子树节点数
- 代价复杂度剪枝 Cost-Complexity Pruning (the weakest link pruning):
使用决策树进行预测
我们将预测空间划分为:
𝑋1,𝑋2,…,𝑋𝑝的可能值的集合,分为𝐽不同的和不重叠的区域,𝑅1,𝑅2,…,𝑅𝐽。
对于每个落在𝑅𝑗区域的观测值,我们做相同的预测,这只是𝑅𝑗中训练观测值的响应值的平均值。
线性模型与树模型的对比

-
图1(Graph 1)展示了当特征与响应变量之间的关系可被线性模型很好拟合时,线性模型的表现优于树模型。
-
图2(Graph 2)展示了树模型拟合的结果,虽然逼近了线性边界,但由于分段结构,表现稍差于线性模型。
-
图3(Graph 3)和图4(Graph 4)展示了特征与响应之间的复杂非线性关系:
- 线性模型(图3)无法很好捕捉这种非线性边界。
- 树模型(图4)通过分区分割能更灵活地拟合复杂形状,表现更合适。
总结:
- 如果数据关系接近线性,线性模型更优。
- 如果数据关系复杂且非线性,树模型更适合。
树模型的优缺点
优点(Advantages)
- 树模型非常容易向人解释。
- 有人认为决策树与人类的决策过程较为接近。
- 树模型可以图形化展示,直观易懂。
- 能处理不同类型的数据,不需要进行数据缩放。
缺点(Disadvantages)
- 树模型的预测准确度通常不及其他一些回归和分类方法。
- prone to over-fitting
树模型集成方法详解
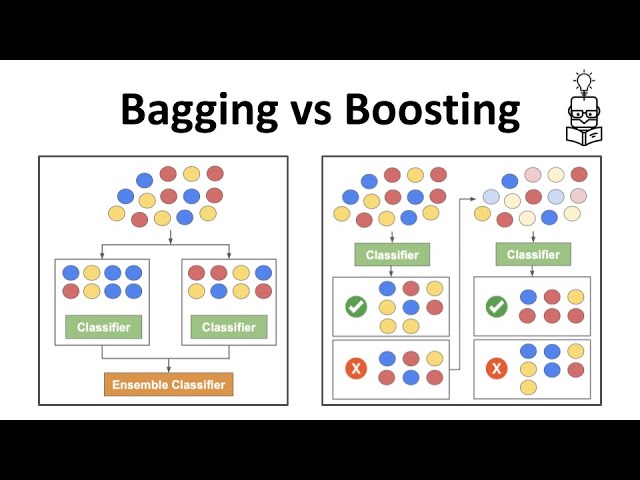
树模型集成(Ensemble of Trees)
- 构建多个决策树
- 结合多个树的结果,形成更稳定、更准确的预测器
关键思想
- 对树进行采样(如自助采样 bootstrap)
- 每次分裂时使用随机子集特征
- 聚合预测结果:
- 分类任务采用多数投票
- 回归任务采用平均值
常用方法
- Bagging:并行构建多棵树并平均结果
- 随机森林(Random Forest):Bagging 加上随机特征选择
- Boosting:序列式构建树以改进误差
集成方法的优势在于通过聚合降低方差,提高模型鲁棒性。
Bagging(Bootstrap Aggregating)
- Bagging是一种降低模型方差的通用方法,特别适用于决策树。
- 原理是对训练数据集进行多次自助采样,生成多个训练子集。
- 对每个子集训练独立的树模型,最终对预测结果求平均。
Bagging的方差原理
- 给定 n n n个独立样本,均值的方差是 σ 2 / n \sigma^2 / n σ2/n。
- 通过平均多个样本,减少方差。
- 由于只有一个训练集,使用bootstrap采样制造多个训练集。
Bagging流程
-
从原始训练集采样 B B B个bootstrap样本。
-
训练 B B B个树模型,记第 b b b个树的预测为 f ^ b ∗ ( x ) \hat{f}_b^*(x) f^b∗(x)。
-
集成预测为:
f ^ ( x ) = 1 B ∑ b = 1 B f ^ b ∗ ( x ) \hat{f}(x) = \frac{1}{B} \sum_{b=1}^B \hat{f}_b^*(x) f^(x)=B1b=1∑Bf^b∗(x)
OOB误差估计(Out-of-Bag Error)
-
由于每棵树仅使用约 2 / 3 2/3 2/3的样本进行训练,剩余 1 / 3 1/3 1/3样本称为OOB样本。
OOB(Out-Of-Bag)样本是在bagging过程中划分的,具体来说:
- 在bagging时,每棵树的训练数据是通过bootstrap采样从原始训练集中随机有放回抽取的一个子样本。
- 由于是有放回抽样,平均而言,大约2/3的样本会被抽到用于训练该树。
- 剩下的约1/3样本没有被抽中,这部分样本就是对应这棵树的OOB样本。
换句话说,OOB样本是bagging抽样后自动形成的,它不是提前划分的固定测试集,而是每棵树“未见过”的样本。
利用这些OOB样本,可以在训练阶段对模型性能进行无偏估计,相当于一种交叉验证。
总结:
OOB样本是在bagging采样时自然划分出来的,属于bagging过程的一部分,而不是在bagging前固定划分的。 -
利用OOB样本对对应未训练该样本的树进行预测,取平均值作为该样本的预测。
-
OOB误差相当于一种留一交叉验证(LOO CV)误差估计,且计算方便。
随机森林(Random Forest)
- 随机森林在Bagging基础上,增加分裂时随机选取 m m m个特征作为候选变量。
- 每次分裂只从这 m m m个特征中选最佳分裂变量,降低树间相关性,进一步减少方差。
- 通常 m ≈ p m \approx \sqrt{p} m≈p,其中 p p p为总特征数。
随机森林伪代码
设置模型数B
for i = 1 to B:
生成bootstrap样本
训练决策树:
每次分裂:
从p个特征中随机选m个
选择最佳分裂特征
endfor
Boosting方法
- Boosting是另一种集成思想,树模型按序列顺序依次训练。
- 每棵树使用之前树的错误信息,重点拟合残差。
- 通过逐步修正误差,提高整体预测性能。
Boosting基本思想
- 与Bagging不同,Boosting模型是依赖的序列结构。
- 最终模型为多个弱学习器的加权和。
- 通过学习率 λ \lambda λ控制每一步改进的幅度,防止过拟合。
Boosting流程(回归树示例)
-
初始化预测模型 f ^ ( 0 ) ( x ) = 0 \hat{f}^{(0)}(x) = 0 f^(0)(x)=0,残差 r i = y i r_i = y_i ri=yi。
-
对 b = 1 , . . . , B b=1,...,B b=1,...,B:
-
拟合树模型 f ^ b \hat{f}_b f^b到残差 r r r。
-
更新模型:
f ^ ( b ) ( x ) = f ^ ( b − 1 ) ( x ) + λ f ^ b ( x ) \hat{f}^{(b)}(x) = \hat{f}^{(b-1)}(x) + \lambda \hat{f}_b(x) f^(b)(x)=f^(b−1)(x)+λf^b(x) -
更新残差:
r i ← r i − λ f ^ b ( x i ) r_i \leftarrow r_i - \lambda \hat{f}_b(x_i) ri←ri−λf^b(xi)
-
-
最终模型为所有加权树的和。
需要调节的参数
- 树的个数 B B B
- 学习率 λ \lambda λ(通常为0.001到0.01)
- 树的深度 d d d(如 d = 1 d=1 d=1即树桩)
其他Boosting变体
- AdaBoost:针对分类,重加权错误样本,组合弱分类器。
- 随机梯度提升(Stochastic Gradient Boosting):每次迭代使用训练集子样本,增强泛化能力。
- XGBoost:高效的梯度提升实现,支持正则化,处理缺失值,广泛应用。
Bagging与Boosting对比
| 特性 | Bagging | Boosting |
|---|---|---|
| 学习器训练方式 | 独立、并行 independently | 序列式依赖 sequentially |
| 树的复杂度 | 复杂树 | 通常为弱学习器(树桩) |
| 参数调节 | 参数较少 | 参数较多,需细调 |
| 目标 | 降低方差 | 降低偏差和方差 |
总结
- 决策树简单易解释,但单棵树性能有限。
- Bagging通过并行构建多棵树降低方差。
- 随机森林在Bagging基础上增加特征随机化,进一步提升性能。
- Boosting通过序列训练和残差拟合,提升预测准确度。
- 随机森林和Boosting是监督学习中效果领先的方法,但解释性较弱。
- 可通过变量重要性(如基尼指数减少)评估特征影响。