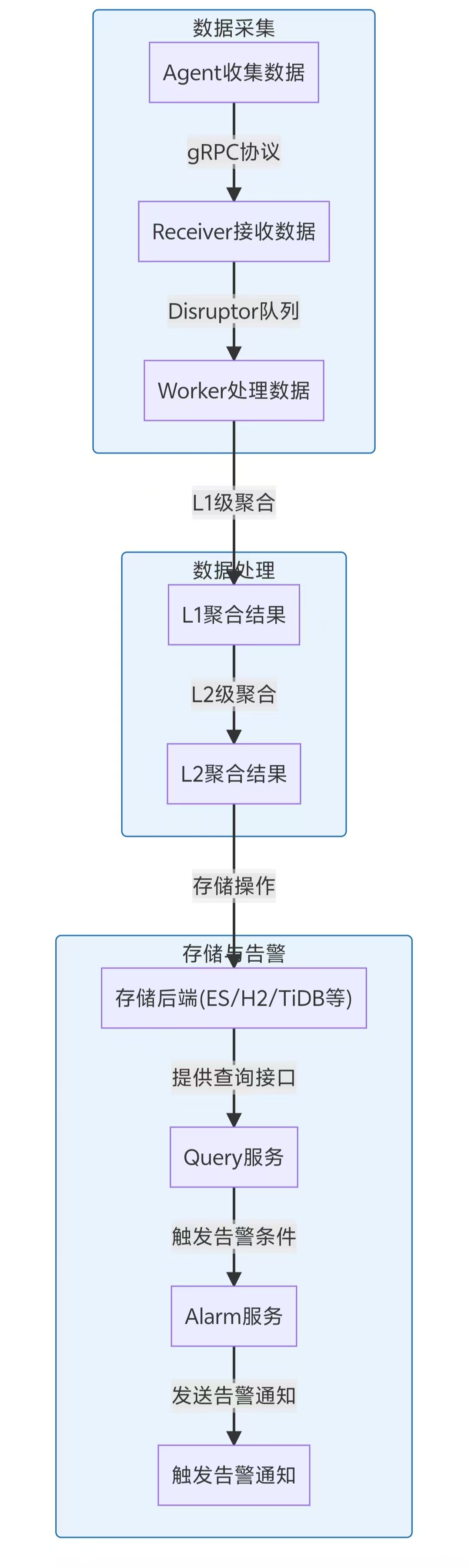
算法概览

排序算法	平均时间复杂度	最坏时间复杂度	空间复杂度	稳定性	适用场景
插入排序	O(n²)	O(n²)	O(1)	稳定	小规模/基本有序
希尔排序	O(n log n)	O(n²)	O(1)	不稳定	中等规模
冒泡排序	O(n²)	O(n²)	O(1)	稳定	教学/小规模
堆排序	O(n log n)	O(n log n)	O(1)	不稳定	大规模数据
选择排序	O(n²)	O(n²)	O(1)	不稳定	小规模
快速排序	O(n log n)	O(n²)	O(log n)	不稳定	通用场景
归并排序	O(n log n)	O(n log n)	O(n)	稳定	大数据/外部排序
计数排序	O(n+k)	O(n+k)	O(k)	稳定	整数/小范围数据

一、插入排序（Insertion Sort）

原理与特点

插入排序的工作方式类似于整理扑克牌：将未排序元素逐个插入到已排序序列的正确位置。它的优势在于处理小规模或基本有序数据时效率高。

void InsertSort(int* a, int n) {
    for(int i = 0; i < n - 1; i++) {
        int end = i;
        int tmp = a[end + 1];  // 待插入元素
        // 寻找插入位置并移动元素
        while (end >= 0) {
            if (a[end] > tmp) {
                a[end + 1] = a[end];  // 元素后移
                end--;
            } else break;
        }
        a[end + 1] = tmp;  // 插入元素
    }
}

特点分析：

• 稳定排序算法

• 自适应：数据越有序，效率越高

• 当n≤1000时效率优于复杂排序算法

二、希尔排序（Shell Sort）

原理与特点

希尔排序是插入排序的改进版，通过将数组分组进行插入排序，逐步减小分组间隔，最终实现整体有序。它突破了O(n²)的时间复杂度瓶颈。

void ShellSort(int* a, int n) {
    int gap = n;
    while(gap > 1) {
        gap = gap / 2;  // 动态缩小间隔
        for (int i = 0; i < n - gap; i++) {
            int end = i;
            int tmp = a[end + gap];
            // 组内插入排序
            while (end >= 0) {
                if (a[end] > tmp) {
                    a[end + gap] = a[end];
                    end -= gap;  // 跨步比较
                } else break;
            }
            a[end + gap] = tmp;
        }
    }
}

特点分析：

• 第一个突破O(n²)的排序算法

• 间隔序列的选择影响效率（本例使用Knuth序列）

• 中等规模数据排序的理想选择

三、冒泡排序

原理与特点

冒泡排序是最基础的排序算法之一，通过不断比较相邻元素并交换位置，使较大元素逐渐"浮"到数组末尾，如同气泡上升的过程。其名称就来源于这种元素移动的特性。

void BubbleSort(int* a, int n) {
    for(int j = 0; j < n; j++) {
        int exchange = 0;  // 交换标志位
        
        // 单趟冒泡：将最大元素移到末尾
        for (int i = 1; i < n - j; i++) {
            // 相邻元素比较交换
            if (a[i - 1] > a[i]) {
                Swap(&a[i - 1], &a[i]);
                exchange = 1;  // 标记发生交换
            }
        }
        
        // 提前终止优化：未发生交换说明已有序
        if (exchange == 0) break;
    }
}

关键优化点

1. 提前终止机制：

   • 通过exchange标志检测是否发生交换

   • 当某趟未发生交换时，说明数组已完全有序

   • 对基本有序数组效率显著提升

2. 逐步缩小范围：

   • 每完成一趟排序，待排序范围缩小一位

   • n - j确保已排序部分不再参与比较

四、堆排序（Heap Sort）

原理与特点

利用堆数据结构实现的排序算法，通过构建大顶堆，不断将堆顶元素（最大值）与末尾元素交换，然后调整剩余元素为堆。

// 向下调整堆
void AdjustDown(int* a, int n, int parent) {
    int child = parent * 2 + 1;
    while (child < n) {
        // 选择较大的子节点
        if (child + 1 < n && a[child] < a[child + 1]) 
            child++;
        // 父子节点交换
        if (a[child] > a[parent]) {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        } else break;
    }
}

void HeapSort(int* a, int n) {
    // 从最后一个非叶节点建堆
    for (int i = (n - 1 - 1) / 2; i >= 0; i--) 
        AdjustDown(a, n, i);
    
    // 排序过程
    int end = n - 1;
    while (end > 0) {
        Swap(&a[0], &a[end]);  // 堆顶元素移到末尾
        AdjustDown(a, end, 0);  // 调整剩余堆
        end--;
    }
}

特点分析：

• 原地排序，空间复杂度O(1)

• 适合处理超大规模数据

• 常用于优先级队列实现

 

五、快速排序（Quick Sort）

原理与特点

采用分治策略的排序算法，通过选取基准值将数组划分为两个子数组，递归排序子数组。

 经典实现（双指针法）

void QuickSort(int* a, int left, int right) {
    if (left >= right) return;
    
    if (right - left + 1 < 10) {  // 小区间优化
        InsertSort(a + left, right - left + 1);
    } else {
        int midi = GetMidi(a, left, right);
        Swap(&a[left], &a[midi]);  // 基准值放最左
        
        int keyi = left;
        while (left < right) {
            while (left < right && a[right] >= a[keyi]) right--;
            while (left < right && a[left] <= a[keyi]) left++;
            Swap(&a[left], &a[right]);
        }
        Swap(&a[left], &a[keyi]);  // 基准值归位
        QuickSort(a, begin, left - 1);  // 递归左子数组
        QuickSort(a, left + 1, end);    // 递归右子数组
    }
}

 前后指针法（更高效）

void QuickSort2(int* a, int left, int right) {
    if (left >= right) return;
    
    int keyi = left;
    int prev = left, cur = left + 1;
    while (cur <= right) {
        if (a[cur] < a[keyi] && ++prev != cur)
            Swap(&a[prev], &a[cur]);
        cur++;
    }
    Swap(&a[keyi], &a[prev]);  // 基准值归位
    QuickSort2(a, left, prev - 1);
    QuickSort2(a, prev + 1, right);
}

六、归并排序（Merge Sort）

原理与特点

采用分治策略的稳定排序算法，将数组递归分割，然后合并有序子数组。本文提供递归和非递归两种实现。

void _MergeSort(int* a, int begin, int end, int* tmp) {
    if (begin >= end) return;
    
    int mid = (begin + end) / 2;
    // 递归分割
    _MergeSort(a, begin, mid, tmp);
    _MergeSort(a, mid + 1, end, tmp);
    
    // 合并有序数组
    int begin1 = begin, end1 = mid;
    int begin2 = mid + 1, end2 = end;
    int i = begin;
    while (begin1 <= end1 && begin2 <= end2) {
        tmp[i++] = a[begin1] <= a[begin2] 
                 ? a[begin1++] 
                 : a[begin2++];
    }
    // 处理剩余元素
    while (begin1 <= end1) tmp[i++] = a[begin1++];
    while (begin2 <= end2) tmp[i++] = a[begin2++];
    
    memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

void MergeSort(int* a, int n) {
    int* tmp = malloc(sizeof(int) * n);
    _MergeSort(a, 0, n - 1, tmp);
    free(tmp);
}

特点分析：

• 稳定排序算法

• 适合外部排序（大数据文件）

• 链表排序的最佳选择

七、计数排序

void CountSort(int* a, int n) {
    // 确定数据范围
    int min = a[0], max = a[0];
    for (int i = 1; i < n; i++) {
        if (a[i] > max) max = a[i];
        if (a[i] < min) min = a[i];
    }
    int range = max - min + 1;
    
    // 创建计数数组
    int* count = malloc(sizeof(int) * range);
    memset(count, 0, sizeof(int) * range);
    
    // 统计元素频次
    for (int i = 0; i < n; i++) 
        count[a[i] - min]++;
    
    // 回写排序结果
    int j = 0;
    for (int i = 0; i < range; i++) {
        while (count[i]--) 
            a[j++] = i + min;
    }
    free(count);
}

适用场景：

• 数据范围为有限整数

• 数据范围远小于数据量（k << n）

• 需要稳定排序的场景

八、如何选择排序算法

1. 小规模数据：插入排序

2. 通用场景：快速排序（需随机化基准）

3. 内存受限环境：堆排序

4. 稳定排序需求：归并排序

5. 已知数据范围：计数排序

6. 链表排序：归并排序

7. 外部排序：多路归并排序