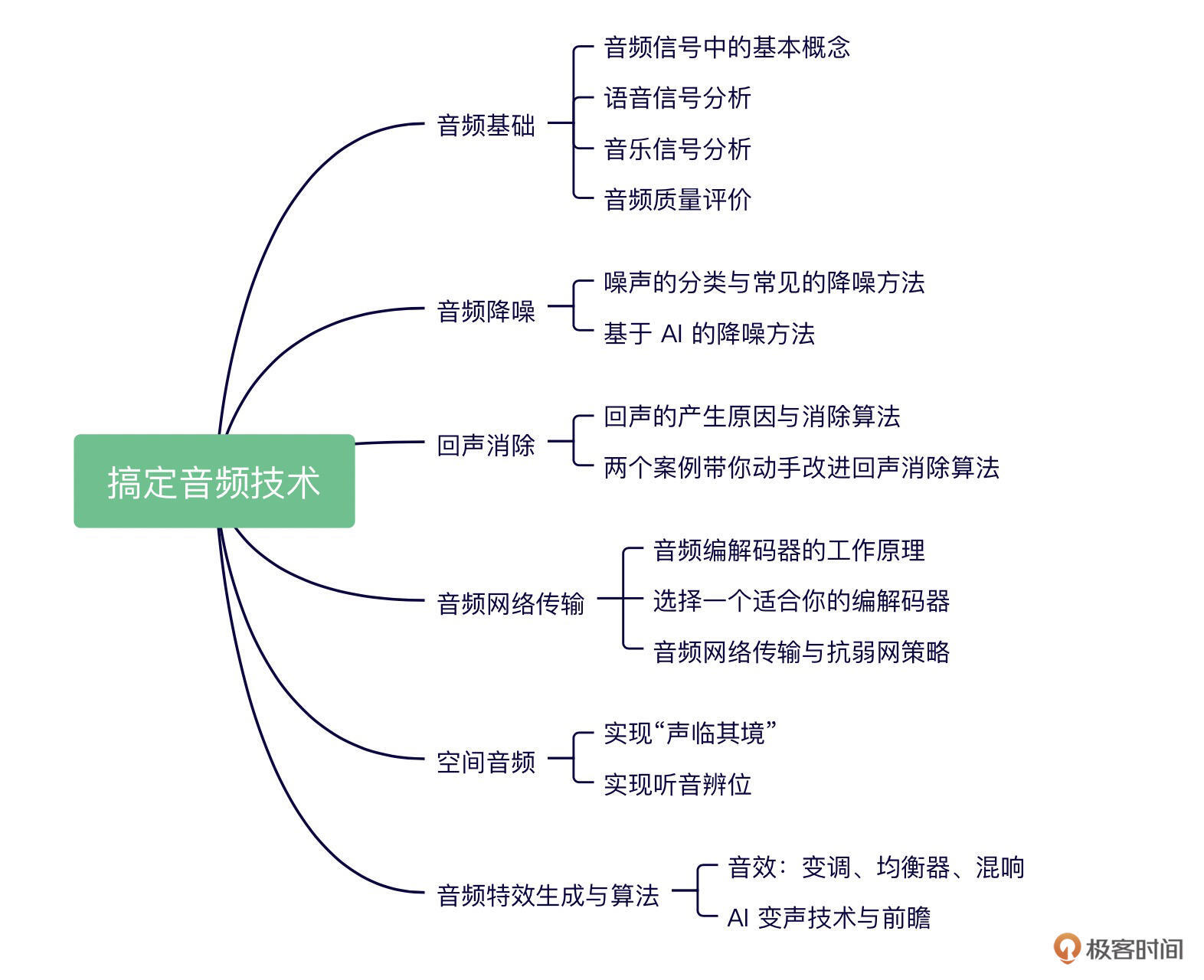
2021年由Hashim等人提出(论文:Honey Badger Algorithm: A New Metaheuristic Algorithm for Solving Optimization Problems)。模拟蜜獾在自然界中的智能捕食行为,属于群体智能优化算法(与粒子群PSO、遗传算法GA同属一类),适用于连续优化问题。
一 行为模型
蜜獾的两种主要行为驱动算法设计:
(1)挖掘模式:
针对地下猎物:通过嗅觉定位 + 动态挖掘路径。
(2)采蜜模式:
跟随导蜜鸟定位蜂巢 → 直接奔袭蜜源。
二 数学模型与迭代步骤
2.1关键变量定义:
蜜獾位置:候选解向量
猎物强度(I):
:个体
的目标函数值(如适应度)
:当前种群中最小和最大函数值,两者做差可以将
进行归一化处理。
:极小常数(防止分母为零)
上述公式代标强度的范围最大是1+,最小是
。
函数值 反映解的质量。优化问题中,
越小(化最小问题)表示解越优,更优解代表更接近全局最优解,代表与“猎物”的隐含距离更小,因此隐含距离越小,强度越小,接近程度越大。
| 个体 | 函数值 F(x)F(x)F(x) | 与最优解距离 | 计算强度 IiI_iIi | 强度 vs 距离关系 |
|---|---|---|---|---|
| A(最优) | 最近 | 强度最小 | ||
| B | 中等 | 强度中等 | ||
| C(最差) | 最远 | 强度最大 |
强度越小越好。
距离大 ⇒ F(xi)差 ⇒ (F(xi)−Fmin) ↑ ⇒ ↑ ⇒ 算法反馈:加大搜索步长
这种设计以极低计算代价实现了蜜獾“嗅到远距离猎物时采取更大动作”的生物智能模拟。
为什么不用几何距离?
避免高维距离计算、函数值差距能推广到离散/非几何空间,泛用性高、算法运行中已计算 ,复用数据无需额外开销,效率高。
2.2探索阶段(Exploration)- 气味扩散
基于猎物强度的全局搜索:
:当前最佳猎物位置
:控制搜索方向(±1随机切换)
:随机向量
:密度因子(随迭代递减)
强度的作用:
大(解质量差、距离远)→ 乘以
后步长增大 → 加强全局探索
小(解质量好、距离近)→ 乘以
后步长减小 → 精细局部开发
2.3开发阶段(Exploitation)- 精确捕食
局部挖掘(模拟蜜獾洞穴内捕猎):
:随机向量
:个体到猎物的距离
通过密度因子 动态平衡探索与开发:
( 为常数,
为当前迭代,
为最大迭代)
决策规则:若 (
为切换阈值),使用挖掘模式;否则使用采蜜模式。
三 实现方法
3.1过程示例
初始化种群位置 x_i, i=1,2,...,N
计算适应度值 F(x_i)
while t < T_max:
更新密度因子 α
计算猎物强度 I_i
for each 蜜獾个体:
if rand < δ:
执行探索阶段(气味扩散)
else:
执行开发阶段(挖掘捕食)
更新当前位置 x_i
计算新适应度 F(x_i)
更新全局最优解 x_prey
t = t + 1
返回最优解 x_prey
3.2参数设置
| 参数 | 意义 | 推荐值 |
|---|---|---|
| 种群规模 | 30~50 | |
| 模式切换阈值 | 0.8 | |
| 密度衰减常数 | 2.0 | |
| 最大迭代次数 | 100~500 |
3.3优势和局限性
| 优势 | 局限性 |
|---|---|
| 全局探索能力强(气味机制) | 对高维问题敏感 |
| 局部开发高效(动态密度因子) | 参数需经验调整(如δ) |
| 收敛速度快于传统算法(PSO等) | 易陷局部最优的改进变体 |
| 代码实现简单 |
四 应用场景
工程优化:结构设计、PID控制器调参
人工智能:神经网络超参数优化
能源管理:光伏阵列最大功率点跟踪(MPPT)
研究方向:离散化改进(如HBA-TSP)、多目标版本(MO-HBA)
五 在CEC2017测试函数集上使用HBA的python代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
class HBA:
def __init__(self, obj_func, dim=30, pop_size=100, max_iter=1000, lb=-100, ub=100, C=2, delta=0.8):
"""
蜜獾算法 (Honey Badger Algorithm)
参数:
obj_func -- 目标函数
dim -- 问题维度
pop_size -- 种群大小
max_iter -- 最大迭代次数
lb -- 变量下界
ub -- 变量上界
C -- 密度因子常数
delta -- 模式切换阈值
"""
self.obj_func = obj_func
self.dim = dim
self.pop_size = pop_size
self.max_iter = max_iter
self.lb = lb
self.ub = ub
self.C = C
self.delta = delta
# 初始化种群
self.positions = np.random.uniform(lb, ub, (pop_size, dim))
self.fitness = np.zeros(pop_size)
self.best_position = np.zeros(dim)
self.best_fitness = np.inf
self.convergence_curve = np.zeros(max_iter)
def evaluate(self):
"""评估所有个体适应度"""
for i in range(self.pop_size):
self.fitness[i] = self.obj_func(self.positions[i])
if self.fitness[i] < self.best_fitness:
self.best_fitness = self.fitness[i]
self.best_position = self.positions[i].copy()
def optimize(self):
"""执行优化过程"""
self.evaluate() # 初始评估
for t in range(self.max_iter):
# 1. 计算猎物强度
f_min = np.min(self.fitness)
f_max = np.max(self.fitness)
I = (self.fitness - f_min) / (f_max - f_min + 1e-25) # 避免除零
I = 1 + I # 确保强度至少为1
# 2. 更新密度因子
alpha = self.C * np.exp(-t / self.max_iter)
# 3. 更新每个个体位置
for i in range(self.pop_size):
# 为每个个体生成随机方向因子
F = 1 if np.random.rand() < 0.5 else -1 # 随机方向(在循环内部重新定义)
if np.random.rand() < self.delta: # 挖掘模式(探索)
r1, r2, r3 = np.random.rand(3) # 只需要3个随机数
# 气味导向的位置更新
new_pos = self.best_position + F * r1 * alpha * I[i] * \
np.abs(np.cos(2 * np.pi * r2) * (1 - np.cos(2 * np.pi * r3)))
else: # 采蜜模式(开发)
r4 = np.random.rand()
# 动态挖掘的位置更新
new_pos = self.best_position + F * r4 * alpha * np.abs(self.best_position - self.positions[i])
# 越界处理
new_pos = np.clip(new_pos, self.lb, self.ub)
# 计算新位置适应度
new_fitness = self.obj_func(new_pos)
# 更新个体位置和适应度
if new_fitness < self.fitness[i]:
self.positions[i] = new_pos
self.fitness[i] = new_fitness
if new_fitness < self.best_fitness:
self.best_position = new_pos.copy()
self.best_fitness = new_fitness
# 记录当前最优解
self.convergence_curve[t] = self.best_fitness
print(f"Iteration {t + 1}/{self.max_iter} - Best Fitness: {self.best_fitness:.6e}")
return self.best_position, self.best_fitness, self.convergence_curve
# ===================== CEC2017测试函数集实现 ========================
def cec17_f1(x):
"""Shifted and Rotated Bent Cigar Function (Function 1)"""
d = len(x)
z = x - 100 # Shift to new optimum
rotated_z = z @ rot_matrix[d] if d in rot_matrix else z # Rotation
return rotated_z[0] ** 2 + 1e6 * np.sum(rotated_z[1:] ** 2) + 100
def cec17_f3(x):
"""Shifted and Rotated Rosenbrock's Function (Function 3)"""
d = len(x)
z = 0.5 * (x - 40) # Shift and scale
rotated_z = z @ rot_matrix[d] if d in rot_matrix else z # Rotation
sum_val = 0
for i in range(d - 1):
sum_val += 100 * (rotated_z[i] ** 2 - rotated_z[i + 1]) ** 2 + (rotated_z[i] - 1) ** 2
return sum_val + 300
def cec17_f5(x):
"""Shifted and Rotated Ackley's Function (Function 5)"""
d = len(x)
z = x + 50 # Shift to new optimum
rotated_z = (z @ rot_matrix[d]) if d in rot_matrix else z # Rotation
sum1 = np.sum(rotated_z ** 2)
sum2 = np.sum(np.cos(2 * np.pi * rotated_z))
return -20 * np.exp(-0.2 * np.sqrt(sum1 / d)) - np.exp(sum2 / d) + 20 + np.e + 500
# ===================== 辅助函数 ========================
def generate_rotation_matrix(dim):
"""生成随机旋转矩阵(模拟CEC2017的旋转特性)"""
H = np.random.randn(dim, dim)
Q, R = np.linalg.qr(H)
return Q
def plot_results(convergence, func_name, dim):
"""绘制收敛曲线"""
plt.figure(figsize=(10, 6))
plt.semilogy(convergence, 'b-', linewidth=2)
plt.title(f'HBA on {func_name} - Dimension {dim}\nFinal Fitness: {convergence[-1]:.4e}', fontsize=12)
plt.xlabel('Iteration', fontsize=12)
plt.ylabel('Fitness (log scale)', fontsize=12)
plt.grid(True, which='both', linestyle='--')
plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True))
plt.tight_layout()
plt.show()
# ===================== 主程序 ========================
if __name__ == "__main__":
# 实验参数
dim = 30 # 问题维度
max_iter = 1000 # 最大迭代次数
pop_size = 100 # 种群大小
# 预生成旋转矩阵 (模拟CEC2017特性)
np.random.seed(42)
rot_matrix = {
dim: generate_rotation_matrix(dim)
}
# 定义要测试的函数
test_functions = {
"CEC2017 F1 (Bent Cigar)": cec17_f1,
"CEC2017 F3 (Rosenbrock)": cec17_f3,
"CEC2017 F5 (Ackley)": cec17_f5
}
# 对每个测试函数运行HBA
results = {}
for name, func in test_functions.items():
print(f"\n{'=' * 80}")
print(f"Optimizing Function: {name}")
print(f"{'=' * 80}")
# 初始化并运行HBA
optimizer = HBA(
obj_func=func,
dim=dim,
pop_size=pop_size,
max_iter=max_iter,
lb=-100,
ub=100
)
best_sol, best_fit, convergence = optimizer.optimize()
results[name] = convergence
# 打印最终结果
print(f"\n{'*' * 80}")
print(f"{name} Optimization Result:")
print(f"Best Solution: {best_sol[:5]}...") # 只打印前5维
print(f"Best Fitness: {best_fit:.6e}")
print(f"Optimal Value Found: {func(best_sol):.6e}")
print(f"{'*' * 80}\n")
# 绘制收敛曲线
plot_results(convergence, name, dim)
# 比较所有函数的收敛曲线
plt.figure(figsize=(12, 8))
for name, conv in results.items():
plt.semilogy(conv, label=name, linewidth=2)
plt.title(f'HBA Performance on CEC2017 Functions (Dim={dim})', fontsize=16)
plt.xlabel('Iteration', fontsize=12)
plt.ylabel('Fitness (log scale)', fontsize=12)
plt.legend(fontsize=12)
plt.grid(True, which='both', linestyle='--')
plt.tight_layout()
plt.savefig('hba_cec2017_convergence.png', dpi=300)
plt.show()
输出值为:


 通过增加迭代次数和种群大小可以更加接近最优解。
通过增加迭代次数和种群大小可以更加接近最优解。