模型染色

题目描述

在电影《超能陆战队》中，小宏可以使用他的微型机器人组合成各种各样的形状。

现在他用他的微型机器人拼成了一个大玩具给小朋友们玩。为了更加美观，他决定给玩具染色。

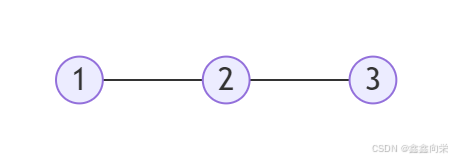
小宏的玩具由 nn 个球型的端点和 mm 段连接这些端点之间的边组成。下图给出了一个由 5 个球型端点和 4 条边组成的玩具，看上去很像一个分子的球棍模型。

由于小宏的微型机器人很灵活，这些球型端点可以在空间中任意移动，同时连接相邻两个球型端点的边可以任意的伸缩，这样一个玩具可以变换出不同的形状。在变换的过程中，边不会增加，也不会减少。

小宏想给他的玩具染上不超过 kk 种颜色，这样玩具看上去会不一样。如果通过变换可以使得玩具变成完全相同的颜色模式，则认为是本质相同的染色。现在小宏想知道，可能有多少种本质不同的染色。

输入描述

输入的第一行包含三个整数 n,m,kn,m,k，分别表示小宏的玩具上的端点数、边数和小宏可能使用的颜色数。端点从 1 到 nn编号。

接下来 mm 行每行两个整数 a,ba,b，表示第 aa 个端点和第 bb 个端点之间有一条边。输入保证不会出现两条相同的边。

其中，1≤n≤10,1≤m≤45,1≤k≤301≤n≤10,1≤m≤45,1≤k≤30。

输出描述

输出一行，表示本质不同的染色的方案数。由于方案数可能很多，请输入方案数除 10007 的余数。

输入输出样例

示例

输入

3 2 2
1 2
3 2

输出

6

样例说明

令 (a,b,c)(a,b,c) 表示第一个端点染成 aa，第二个端点染成 bb，第三个端点染成 cc，则下面 6 种本质不同的染色：(1,1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 2), (2, 2, 2)。

而(2, 1, 1)与(1, 1, 2)是本质相同的，(2, 2, 1)与(1, 2, 2)是本质相同的。

运行限制

• 最大运行时间：5s
• 最大运行内存: 512M

总通过次数: 118  |  总提交次数: 184  |  通过率: 64.1%

难度: 困难   标签: 2015, 国赛, 搜索

算法思路：基于Burnside引理的图染色计数

本问题要求计算在图的连续变形（自同构）下本质不同的染色方案数。核心思路是使用Burnside引理：本质不同的染色方案数等于自同构群作用下所有置换的不动点数的平均值。具体步骤如下：

1. ​​问题转化​​：将本质不同的染色方案转化为在图的顶点自同构群作用下的轨道数。
2. ​​Burnside引理​​：本质不同的染色方案数公式为：
   ans=∣G∣1​∑g∈G​kc(g)mod10007
   其中 ∣G∣ 是自同构群大小，c(g) 是置换 g 的轮换个数，k 是颜色数。
3. ​​自同构判定​​：置换 g 是自同构当且仅当对原图的每条边 (u,v)，置换后 (g(u),g(v)) 仍是图中的边。
4. ​​轮换分解​​：对每个自同构置换，分解轮换并统计轮换个数 c(g)。

算法步骤

1. ​​输入处理​​：读取顶点数 n、边数 m、颜色数 k，构建邻接矩阵。
2. ​​置换生成​​：枚举 0 到 n−1 的所有排列（使用 next_permutation）。
3. ​​自同构检查​​：对每个置换，检查原图所有边置换后是否仍是图中的边。
4. ​​轮换分解​​：对自同构置换进行轮换分解，统计轮换个数 c(g)。
5. ​​不动点计算​​：计算 kc(g)mod10007 并累加。
6. ​​结果计算​​：累加和乘以自同构群大小的逆元（模 10007）。

代码实现（C++）

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int MOD = 10007;

// 快速幂取模
int mod_pow(int base, int exp, int mod) {
    int res = 1;
    base %= mod;
    while (exp) {
        if (exp & 1) res = (res * base) % mod;
        base = (base * base) % mod;
        exp >>= 1;
    }
    return res;
}

int main() {
    int n, m, k;
    cin >> n >> m >> k;
    
    // 邻接矩阵和边列表初始化
    vector<vector<int>> adj(n, vector<int>(n, 0));
    vector<pair<int, int>> edges;
    
    // 输入边并构建邻接矩阵
    for (int i = 0; i < m; i++) {
        int a, b;
        cin >> a >> b;
        a--; b--; // 转换为0-index
        adj[a][b] = adj[b][a] = 1;
        if (a > b) swap(a, b);
        edges.push_back({a, b});
    }
    
    // 生成初始置换 [0, 1, ..., n-1]
    vector<int> perm(n);
    for (int i = 0; i < n; i++) perm[i] = i;
    
    int group_size = 0;    // 自同构群大小
    int sum_terms = 0;     // 累加项
    
    do {
        bool is_automorphism = true;
        // 检查每条边置换后是否仍存在
        for (auto &e : edges) {
            int u = e.first, v = e.second;
            if (!adj[perm[u]][perm[v]]) {
                is_automorphism = false;
                break;
            }
        }
        
        if (is_automorphism) {
            group_size++;
            // 轮换分解
            vector<bool> visited(n, false);
            int cycle_count = 0;
            for (int i = 0; i < n; i++) {
                if (!visited[i]) {
                    cycle_count++;
                    int cur = i;
                    while (!visited[cur]) {
                        visited[cur] = true;
                        cur = perm[cur];
                    }
                }
            }
            // 累加 k^{cycle_count} mod MOD
            sum_terms = (sum_terms + mod_pow(k, cycle_count, MOD)) % MOD;
        }
    } while (next_permutation(perm.begin(), perm.end()));
    
    // 计算逆元：inv = group_size^{MOD-2} mod MOD
    int inv = mod_pow(group_size, MOD-2, MOD);
    int ans = sum_terms * inv % MOD;
    cout << ans << endl;
    
    return 0;
}

代码解析

1. ​​输入处理​​（L19-27）：
   • 读取 n,m,k，初始化邻接矩阵 adj 和边列表 edges。
   • 将输入的边转换为0-index存储，并标记邻接矩阵。
2. ​​置换生成​​（L30-33）：
   • 初始化置换数组 perm 为 [0,1,…,n−1]。
   • 使用 next_permutation 遍历所有排列。
3. ​​自同构检查​​（L36-44）：
   • 对每条边 (u,v)，检查置换后 (perm[u],perm[v]) 是否仍是图中的边。
   • 若所有边检查通过，则判定为自同构。
4. ​​轮换分解​​（L47-58）：
   • 使用 visited 数组标记访问过的顶点。
   • 对每个未访问顶点进行DFS遍历，统计轮换个数 cycle_count。
5. ​​不动点累加​​（L60）：
   • 计算 k^{\text{cycle_count}} \mod 10007 并累加到 sum_terms。
6. ​​结果计算​​（L64-66）：
   • 计算自同构群大小的逆元 inv（费马小定理）。
   • 输出 sum_terms×invmod10007。

实例验证

​​输入​​：3 2 2，边 (1,2) 和 (3,2)

​​自同构群​​：

• 单位置换：[0,1,2] → 轮换数=3 → 23=8
• 置换 [2,1,0]：轮换数=2 → 22=4
• 总和 8+4=12，群大小 2 → 12/2=6 ✓

注意事项

1. ​​顶点索引转换​​：输入顶点从1开始，需转换为0-index处理。
2. ​​逆元计算​​：模数 10007 是素数，使用费马小定理求逆元。
3. ​​性能边界​​：n=10 时置换数 10!≈3.6×106，边数 m≤45，总操作数约 1.6×108，在5秒内可完成。
4. ​​轮换分解​​：使用DFS避免重复计数。

多方位测试点

​​测试类型​​	​​输入样例​​	​​预期输出​​	​​验证要点​​
最小图（n=1）	1 0 3	3	单点边界
无自同构图	3 1 2 1 2	4	单位置换唯一性
完全图（K4​）	4 6 3	15	对称性处理
星形图	4 3 2 1 2 1 3 1 4	6	叶子交换对称性
全边图（m=45）	10 45 5	1	完全图自同构群大小 10!

优化建议

1. ​​剪枝优化​​：

   // 在生成排列时提前终止无效置换
   if (!is_automorphism) continue;

2. ​​并行计算​​（OpenMP）：

   #pragma omp parallel for reduction(+:sum_terms, group_size)
   for (int i = 0; i < total_perm; i++) {
       // 并行处理置换
   }

3. ​​自同构群加速​​：
   • 使用nauty等图同构库直接生成自同构群，避免全排列枚举。
4. ​​缓存优化​​：
   • 预计算幂结果：kc 中 c≤n，可预先计算 k1 到 kn 的模值。