Sparse Crosscoders for Cross-Layer Features and Model Diffing

Abstract

本说明介绍了稀疏跨编码器(sparse crosscoders)，它是一种稀疏自编码器(sparse autoencoders)或transcoders的变体，旨在用于理解叠加中的模型结构。SAEs是在单一层中编码和预测激活值，transcoders则使用某一层的激活来预测下一层的激活，而crosscoders则可以读取和写入多个层。

Crosscoders可以在多个层甚至多个模型之间提取共享特征，具有以下几个应用场景：

1. 跨层特征：Crosscoders将特征视为在多个层之间传播，从而解决跨层叠加问题，并跟踪残差流中持续存在的特征。
2. 路径简化：通过跟踪在残差流中持续存在的特征，crosscoders可以从分析中剔除“重复特征”，允许特征在多个不重要的恒等路径连接中“跳跃”，从而整体上简化路径结构。
3. 模型差异分析：Crosscoders可以在多个模型间提取共享的特征集。这包括同一模型在训练或微调过程中的变化，也包括结构完全不同的独立模型之间的比较。

本说明将首先介绍一些激发crosscoders设计的理论示例，随后展示其在跨层叠加和模型差异分析中的初步实验结果。我们还将简要讨论crosscoders如何有助于简化路径分析的理论，但相关结果将留待后续更新中详述。

1 Motivating Examples

1.1 Cross-Layer Superposition

根据叠加假设，神经网络通过允许特征之间非正交，从而表示的特征数量超过其神经元数量。这一假设的一个结果是，大多数特征是由多个神经元的线性组合表示的：

图1：在基本的叠加中，一个特征是通过某一层中多个神经元的线性组合计算出来的。

这种跨层传播的叠加概念可能会显得奇怪。但在具有合理层数的 Transformer 中，这实际上是相当自然的。
Transformer 的一个有趣特性是：由于残差流是线性的，可以将其绘制成不同但等价的图结构。下面的图突出了一个观点，即两个层可以被看作“几乎是并行的分支”，只不过它们之间多了一条边，使得较早的层可以影响较晚的层。

图2：由于残差流是加性的，在较大的 Transformer 中，相邻的层可以被视为“几乎是并行的”，只是多了一条路径，使得前一层可以影响后一层。

如果考虑一个只需一步就能计算出某个特征的路径，可以想一种实现方式：该路径被拆分到两个层中，但在功能上是并行的。如果模型的层数多于它要计算的路径长度，那么这种实现方式是相当自然的。

图3：
(左2)叠加机制将特征分布在多个神经元上。
(左3)如果我们以“几乎并行分支”的形式绘制 Transformer，自然会想到这些神经元可以存在于不同的层中。
(左4)普通的 Transformer 形式中，这种结构看起来是这样的。

如果特征是由多层共同表示的，并且其中一部分激活可以理解为并行存在的，那么将字典学习方法联合应用于这些层就是一种自然的做法。将这种设置称为crosscoder。

图4：如果将相邻的层视为“几乎并行的分支”，且它们之间可能存在叠加现象，那么将字典学习联合应用于这些层就是一种自然而然的做法。

当模型确实具有带有跨分支叠加的并行分支时，对多个向量联合应用字典学习正是本文所做的事情。

1.2 Persistent Features and Circuit Complexity

当存在跨层叠加时，crosscoders可以派上用场，但当一个计算出的特征在残差流中持续存在多层时，它们同样也能发挥作用。
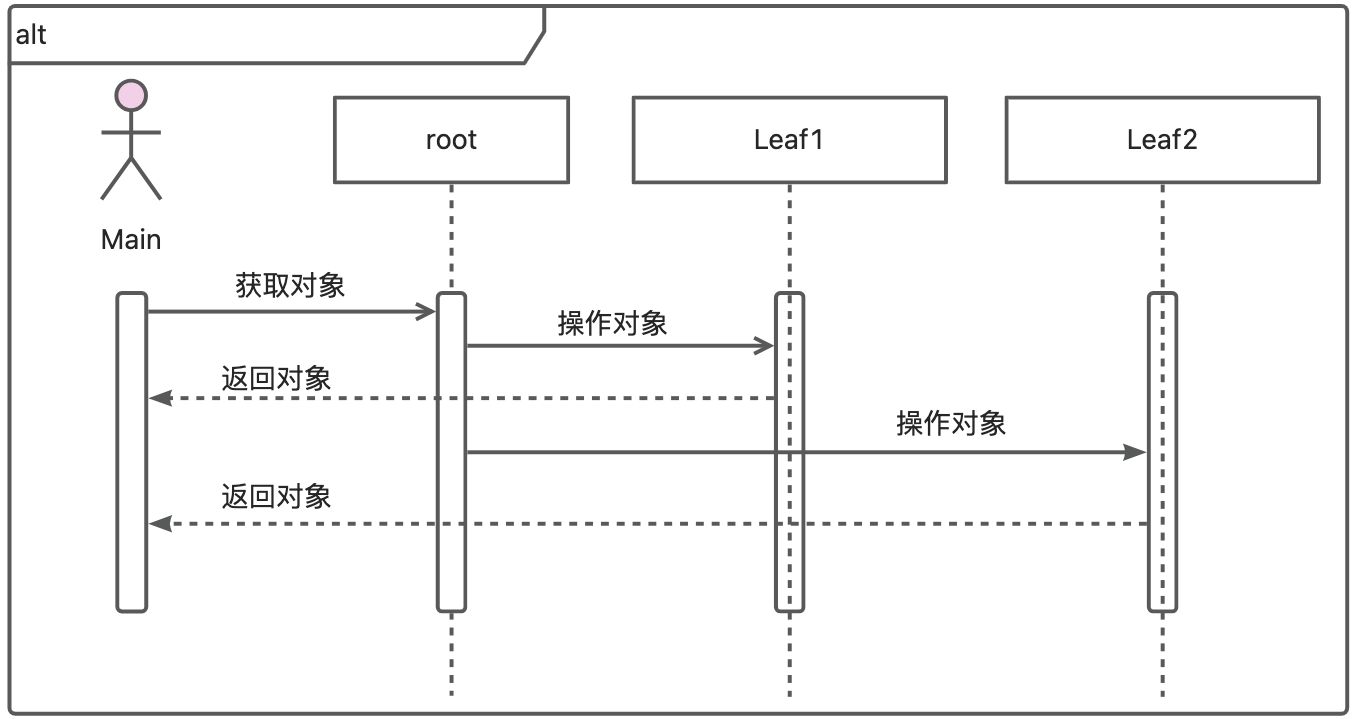
请考虑以下通过残差流的假设“特征生命周期”：

图5。

如果试图从每一层的残差流特征角度来理解这个过程，就会在各层之间出现大量重复的特征。这可能导致路径看起来比实际需要的复杂得多，如图6所示。

图6。

这意味着，如果我们采用合适的架构，比如如上图所示，让特征编码器从单一的残差流层读取信息，而解码器写入到下游层，crosscoder也可能提供一种极大简化路径的策略。

举个例子，假设我们有特征$i$，它的编码器位于第10层；还有特征$j$，它的编码器位于第1层（但解码器会投影到所有后续层）。假设我们通过消融实验、梯度归因或其他方法确定，特征$i$的激活强烈归因于特征$j$中解码到第10层的部分。Crosscoder允许我们立即“跳回去”，将这种归因直接分配给在第1层计算出的特征$j$的激活，而不是通过一连串每层的SAE传播同一基础特征$i$来归因。这样做，有可能发现那些深度远小于模型层数的路径。

不过，这种方法存在一些概念上的风险——它提供的因果描述很可能与底层模型的真实因果关系不同。

2 Crosscoder Basics

SAEs对单层的激活进行编码和预测，而transcoders则利用一层的激活来预测下一层的激活，crosscoders则可以读取和写入多层。
可以将SAEs和transcoders看作是crosscoders的特例。

图7

交叉编码器的基本设置如下。
首先，通过对不同层的激活$a^l(x_j)$($l\in L$)的贡献求和，计算数据点$x_j$上的特征的激活向量$f(x_j)$：
$$f(x_j)=\text{ReLU}(\sum _{l\in L}{W}_{\text{enc}}^l{a}^l(x_j)+b_{\text{enc}})\text{\hspace{1em}(1)}$$
其中$W_{\text{enc}}^l$是layer $l$的编码器权重，$a^l(x_j)$是layer $l$在数据点$x_j$处的激活。
尝试来重建layer $l$中近似的$a^{l^{\prime }}(x_j)$激活值：
$$a^{l^{\prime }}(x_j)=W_{\text{dec}}^{l}f(x_j)+b_{\text{dec}}^l\text{\hspace{1em}(2)}$$
损失函数：
$$L=\sum _{l\in L}\Vert a^l(x_j)-a^{l^{\prime }}(x_j){\Vert }^2+\sum _{l\in L}\sum _i{f}_i(x_j)\Vert W_{\text{dec},i}^l\Vert \text{\hspace{1em}(3)}$$
正则化项可以改写为：
$$\sum _{l\in L}\sum _i{f}_i(x_j)\Vert W_{\text{dec},i}^l\Vert =\sum _i{f}_i(x_j)(\sum _{l\in L}\Vert W_{\text{dec},i}^l\Vert )\text{\hspace{1em}(4)}$$
用每层解码器权重范数的L1范数(${\sum }_{l\in L}\Vert W_{\text{dec},i}^l\Vert$)，其中 $\Vert W_{\text{dec},i}^l\Vert$ 是模型某一层中单个特征解码器向量的L2范数。与用每层范数的 L2 范数($\sqrt{{\sum }_{l\in L}\Vert W_{\text{dec},i}^l{\Vert }^2}$) 相比，使用L1的好处有以下两点：

1. 基线损失对比：L1 范数版本使得 crosscoder 与单层 SAE（或 transcoder）之间的损失可以进行直接比较——crosscoder 的损失可以直接与在相同层上训练的每层 SAE 损失之和进行比较。如果我们改用 L2 范数版本，crosscoder 所得到的损失会远低于每层 SAE 损失之和，因为它通过将特征分布到多个层中，实质上获得了一个“损失减免”的优势。
2. 逐层稀疏性揭示层特异特征：使用 L2 版本会鼓励特征在多个层中展开分布，因为一旦某个特征在某些层上已有非零的解码器范数，再扩展到更多层时对整体 L2 范数的增幅就会减小。相比之下，L1 范数版本不会显式鼓励特征在层之间“扩散”。在实际中，我们发现，在模型差异对比（model diffing）任务中，L1 范数版本有时能更有效地揭示感兴趣的现象——特别是它能同时揭示出共享特征和模型特异特征，而 L2 范数版本往往只能揭示共享特征。

另一方面，L2 范数版本在优化模型所有层的 MSE 与全局 L0 之间的权衡边界方面更有效。因此，在一些应用中，如果不需要揭示特定层或特定模型的特征，也不需要将损失值与每层 SAE 进行比较，那么 L2 范数版本可能更为合适。在本报告中，所有实验均采用了 L1 范数版本。

2.1 Crosscoder Variants

上述这个基础版本称之为“非因果型 crosscoder”。实际上有很多变体，尤其是在以下几个关键维度上：

• 跨层方式：使用 crosscoder，还是普通的 SAE？
• 因果性：是否希望采用一种让早期激活预测后期激活的设置，类似于 transcoder？
• 局部性：将 crosscoder 应用于所有层，还是只应用于部分层？又或者应用于来自不同模型的层？
• 目标对象：建模残差流（residual stream）还是各层的输出？
  

图8：跨层方法
(1) Per-Layer SAEs：在每一层要分析的位置训练一个不同的稀疏自动编码器。这是当前的“标准”方法。
(2) Shared SAE：在每一层使用相同的SAEs。这使得跨层特征具有一致的定义，其中一些特征只在某些层存在。然而，这种方式不允许特征在层之间发生旋转（这种旋转在某些情况下确实会发生）。
(3) Sparse Crosscoder (our focus)：稀疏编码器可以与多层进行交互，从而解决跨层叠加问题，并追踪特征在残差流中的传播。它们可以是一个或多个SAEs，并且可以从不同的层读取和写入。

图9：因果关系
(1) 反因果(Acausal)：每个稀疏编码器同时观察并预测过去、现在和未来的各层。通常只使用一个大型编码器。特征不固定在某一特定层上，这对于分析存在哪些特征以及它们如何分布非常方便，但会使路径分析变得非常困难。
(2) 弱因果(Weakly Causal)：每个编码器既接收来自某一层的激活，也预测当前层和未来层的激活。这使得识别哪些特征是真正“新出现”的变得容易，并且对无法被计算出的特征（例如注意力机制中的）更具容错性。路径分析的难度为中等。
(3) 强因果(Strictly Causal)：每个编码器仅接收来自某一层的激活，并只预测未来层的激活。当可行时，这是最适合进行路径分析的设置。这可以被看作是跨层版的transcoder的一种推广。

图10：位置(Locality)
(1) 全局(Global)：每个编码器与所有层进行交互，除非被因果结构所限制。
(2) 局部/卷积层(Local/“Conv”)：每个编码器只与一个有限范围的层进行交互。
(3) 跳跃层(Skip Layer)：Crosscoder 可以跳过某些层以节省计算资源，但这在严格因果的模型中效果不佳。
(4) 跨模型(Cross Model)：Crosscoder 也可以与来自不同模型的层进行交互，以在它们之间构建标准的特征集。

图11：目标(target)
(1) 残差流(Residual Stream)：稀疏编码器预测残差流。
(2) 层输出(Layer Outputs)：稀疏编码器预测在加入残差流之前的 MLP 或注意力模块的输出。它们仍然可以从残差流中读取信息。

在路径研究中，弱因果和强因果的crosscoders都有助于简化特征交互图，但如何对这些分析结果进行可靠验证仍需探讨。
需要注意的是，这里所描述的强因果crosscoders无法捕捉注意力层所执行的计算。正在探索的几种可能性包括：

1. 使用强因果crosscoders来捕捉 MLP 的计算，并将注意力层执行的计算视为线性（通过在给定提示下对经验注意力模式进行条件化）；
2. 将用于 MLP 输出的强因果crosscoders与用于注意力输出的弱因果crosscoders结合使用；
3. 设计可解释的注意力替代层，与强因果crosscoders结合形成一个“替代模型”。

3 Cross-Layer Features

3.1 Performance and Efficiency of Crosscoders vs SAEs.

Crosscoders能否揭示跨层结构？为探究这个问题，首先在一个18层模型的所有残差流激活上训练了一个全局、非因果(acausal)的crosscoder。将其性能与18个分别在每一层残差流上训练的SAEs进行比较。使用固定的 L1 系数作为稀疏性惩罚。

对于每种方法，在训练步数和总特征数量上进行了grid search，以在不同的 FLOPS 预算下选出最优的特征数量。
关注的是：crosscoders/所有 SAE 的总特征数如何影响字典性能，以及训练中使用的计算资源对性能的影响。请注意，对于一个有$L$层的模型，一个拥有$F$个总特征的全局、非因果crosscoder，其训练所需的 FLOPS 与一个由$L$个分别拥有$F$个特征的 SAE 所组成的集合相同（即总共有$L\times F$个特征）。换句话说，一个由若干单层 SAE 组成、总共拥有 F 个字典特征的集合，其训练所需 FLOPS 只有一个拥有$F$个字典特征的crosscoder的$\frac{1}{L}$。因此，如果crosscoder要在 FLOPS 预算下具备竞争力，就必须在“每个特征的效率”上显著优于 SAE。

首先测量两种方法在验证集上的损失（包括 MSE 和由解码器权重加权的 L1 正则项，跨层求和）：

图12

在控制总特征数量一致的情况下，crosscoder在验证损失上明显优于逐层 SAE。
这一结果表明：
各层之间存在显著的冗余结构（即线性相关），而crosscoders能够将其解释为跨层特征。然而，就训练所需的 FLOPS 而言，在达到相同验证损失时，crosscoder的效率低于逐层 SAE，在高计算预算下，其效率大约是 SAE 的一半。

换句话说，在总特征数量固定的情况下，crosscoder能够通过识别各层之间的共享结构，更高效地利用其资源。它可以将多层中相同的特征归并为一个跨层特征，从而释放出资源用于捕捉其他特征。但识别这些结构在训练阶段需要消耗更多计算资源。

不过，验证损失只是衡量crosscoder实用性的一种方式。
由于损失函数将稀疏性惩罚项按各层的解码器范数加权，它实际上衡量的是（特征，层）二元组的稀疏性（即其 L1 松弛形式）。因此，它反映了模型中任意一层是否可以由crosscoder特征稀疏表示得较好，或者由 SAE 特征表示得更好。
然而，也要关注整个模型的所有层的活动是否可以整体地由crosscoder特征稀疏表示得更好，而不是仅看单层表现。

为此，关注每种方法的（MSE，L0）指标，其中 L0 表示非零特征的数量。在逐层 SAE 的情况下，将所有 SAE 的 L0 范数求和。下图展示了在不同训练 FLOPS 预算下、SAE 和crosscoder各自训练损失最优时的（MSE，L0）值。

图13

从这个角度来看，crosscoders相较于逐层 SAE 展现出显著优势。通过整合各层之间的共享结构，crosscoders对整个模型的激活进行了更少冗余（因此更简洁）的分解。理论上，这种结构整合也许可以通过对 SAE 特征的事后分析来实现，例如通过对激活相似的特征进行聚类。但在实践中，这种分析可能较为困难，尤其是由于 SAE 训练中的随机性影响。crosscoders则是在训练阶段就“内嵌”了这种聚类过程。

从整体上总结结果，crosscoders和逐层 SAE 的效率可以从两个方面进行比较：
在重建单层活动时，crosscoders在特征使用的稀疏性和重建误差之间的权衡上能更高效地利用字典特征，但在训练 FLOPS 的使用效率上不如 SAE；
而在重建整个模型活动时，crosscoders通过消除跨层冗余结构，在重建误差与稀疏性之间的权衡中展现出明确的优势。

3.2 Analysis of Crosscoder Features

本节对crosscoder的特征进行了一些基础分析，特别关注特征在各层之间的表现：
(1) crosscoder的特征是否倾向于只出现在少数几层，还是会跨越整个模型？
(2) crosscoder特征的解码器向量方向在各层之间是否保持稳定，或者说相同的特征在不同层是否会指向不同的方向？

针对问题 (1)，下图中绘制了模型各层中 50 个随机抽样的跨编码器特征的解码器权重范数（这些特征的趋势在整体特征集合中具有代表性）。为了便于可视化比较，将每个特征的范数重新缩放，使其最大值为 1。
可以看到，大多数特征在某一特定层达到最大强度，并在较早和较晚的层中逐渐减弱。有时这种衰减很突然，表示特征较为局部化，但更多时候是逐渐变化，许多特征在大多数甚至全部层中仍保有较大的范数。

图14

Crosscoder认为，只要一个特征在不同层中对相同的数据点激活，就属于相同的特征。关键在于，crosscoder允许特征的方向在各层之间发生变化（即“特征漂移”），接下来将看到，这种漂移似乎非常重要。

回到上面的图，特征在多层中逐渐形成的现象是否是跨层叠加(cross-layer superposition)的证据？虽然这确实与该假设一致，但也可能有其他解释。例如，一个特征可以在某一层明确地产生，然后在下一层被放大。要想更有信心地解释特征逐渐形成的意义，还需要更多研究——理想情况下是路径级别的分析。

现在回到最初提出的第二个问题：关于crosscoder特征的嵌入方向。下面是一些具体的跨编码器特征示例，我们展示了：

上方图表：该特征在每一层的解码器范数强度（如前所示）、其强度峰值所处的层、以及该特征在峰值层的解码方向与其他层的解码方向之间的余弦相似度。
下方图表：特征在第 i 层的解码器向量在第 j 层解码器方向上的投影（因此，每个图的对角线表示该特征在每一层的解码器向量范数）。

最左边一列展示的是一个特征，其解码方向在多个层中缓慢漂移，与其范数衰减的空间尺度大致一致；中间一列展示的是一个特征，其解码方向在其具有显著范数的层之间保持较为稳定；最右边一列展示的是一个在整个模型中始终存在的特征，但其解码方向变化非常快。

图15

总体来看，大多数特征的解码方向在各层之间的稳定性远高于随机预期，但它们在各层之间仍存在显著的漂移，即使在特征解码范数仍然较强的层中也是如此。这种具体行为在不同特征之间差异很大。这表明，crosscoder 所发现的跨层特征并不是仅通过残差连接被被动传递的。

在本研究中并未系统分析特征的可解释性。从一些个别观察来看，crosscoder 的特征与SAE的特征在可解释性方面相似，且在某一层中达到峰值的 crosscoder 特征在语义上与在该层训练的稀疏自动编码器所获得的特征类似。计划在未来的研究中对 crosscoder 特征的可解释性进行更严格的评估。

3.3 Masked Crosscoders

3.3.1 Locality Experiments

本文尝试了带有局部掩码的“卷积式” crosscoder 变体，在这种变体中，每个特征被分配一个包含 K 层的局部窗口，负责对这些层进行编码和解码。我们希望这种方法可以在保留 crosscoder 优势的同时，降低 crosscoder 训练时的 FLOPS 开销。

然而，我们发现当我们将卷积窗口 K 从 1（即每层独立 SAE 的情况）逐渐增大到 n_layers（即全局非因果 crosscoder）时，评估损失几乎呈线性变化——没有明显的拐点可以优化性能与计算成本之间的权衡。换句话说，局部掩码 crosscoder 的性能类似于一个更小、但 FLOPS 匹配的全局 crosscoder。

3.3.2 Causality Experiments

还尝试了“弱因果”（weakly causal）crosscoder 架构。特别关注这样一种结构：每个特征被分配一个编码器层 i ——其编码器只读取第 i 层的信息，而其解码器则尝试重建第 i 层及其之后的所有层。
在评估损失性能方面，这种架构的 FLOPS 效率介于每层 SAE（略差）与全局非因果 crosscoder（略好）之间。而在字典大小方面，它的性能比全局 crosscoder 落后了大约 3 到 4 倍。我们认为这种弱因果 crosscoder 架构在电路分析中很有前景（强因果方法似乎也同样具有潜力）。

还进行了初步实验，使用严格因果的cross-layer transcoders：其中每个特征从某一层 L 的残差流中读取信息，并尝试预测该层及其后续所有层(L、L+1、L+2、… NUM_LAYERS)的 MLP 输出。

分析这些特征的解码器范数，它们可以大致分为三类：

• 局部特征：主要预测紧接着的下一个 MLP 输出；
• 全局特征：以大致相同的强度预测所有后续层的 MLP 输出；
• 介于局部与全局之间的中间特征。

图16