算法学习--持续更新

news2025/6/4 5:57:06

算法

2025年5月24日

  • 完成：快速排序、快速排序基数优化、尾递归优化

    • 快排

      public class QuickSort {
    public void sort(int[] nums, int left, int right) {
        if(left>right){
            return;
        }
        int partiton = quickSort(nums,left,right);
        sort(nums,left,partiton-1);
        sort(nums,partiton+1,right);
    }
    int  quickSort(int[] nums, int left, int right) {
        int i = left,j=right;
        while (i<j){
            while (i<j&&nums[left]>=nums[j]) {//TODO nums[left]>nums[j]从大到小排序
                j--;
            }
            while (i<j && nums[left]<nums[i]) {
                i++;
            }
            swap(nums,i,j);
        }
        swap(nums,i,left);
        return left;
    }
    void swap(int[] nums,int left ,int right){
        int temp = nums[left];
        nums[left]= nums[right];
        nums[right] = temp;
    }
}

    • 快速排序基数优化：注意拿到mid之后要与left交换，后续不变。有一个取中位数的新方法

      int mid = midThree(nums, left, right, left + (right - left) / 2);
swap(nums,mid,left);//交换mid和left TODO 交换完成后以后需要用left

      left要与mid交换，后续直接依旧用left做基准。

      可一直用left做基准，通过修改left所对应的值来优化代码。

      int midThree(int[] nums,int num1,int num2,int num3){//取中位数
        int j = nums[num1],k=nums[num2],l=nums[num3];
        if ((j<=k&&j>=l)||(j>=k&&j<=l))
            return num1;
        if ((k<=j && k>=l)||(k>=j&&k<=l))
            return num2;
        return num3;
    }

    • 尾递归优化：排序算法的选择注意是

      //        if (left>right){
//            return;
//        }   TODO 不能写这种形式，原因为这种只计算一遍修改后的right和left并未递归
       while (left<right){//
           
           ...//用partition-left和right-partition来判断，选择短的进行计算
               
       }

leetcode100

1.两数之和easy

  • 暴力解法：开始想的先排序，后再判断target-nums[i]<nums[j],之后的直接不计算，但是这种方法也改了数组的下标，这种方法适合不用找下标的。

    class Solution {
    public int[] twoSum(int[] nums, int target) {
        //暴力 不可排序
        for (int j =0 ;j<nums.length;++j){
            for (int i = j+1; i < nums.length; ++i) {
                if (nums[i]==target-nums[j]){
                    return new int[]{j,i};
                }
            }
        }
        return null;
    }
}

    Arrays.sort(nums);//改变了下标
for (int j =0 ;j<nums.length-1;j++){
    for (int i = j+1; i < nums.length; i++) {
        if (nums[i]<target-nums[j]){
            continue;
        }if (nums[i]==target-nums[j]){
            return new int[]{j,i};
        }else
            break;
    }
}
return null;

    时间复杂度O(N2)—两次嵌套for循环

    空间复杂度O(1)—无需其他数组

    在这里插入图片描述

  • 哈希表：保证下标和数组一一对应，且可以快速找到。

    // TODO 哈希表解法
//写入哈希表 key--数组值  value--小标
//对于每一个 x，我们首先查询哈希表中是否存在 target - x，
// 然后将 x 插入到哈希表中，
HashMap<Integer,Integer> map = new HashMap<>();
for(int i = 0 ; i < nums.length ; i++){
    if (map.isEmpty()||!map.containsKey(target-nums[i]))//先判断是否存在再去放入map
        map.put(nums[i],i);								//可避免Value值一致所导致的key一致
    else
        return new int[]{map.get(target-nums[i]),i};
}
return new int[0];

    由题意可判断，出现两个相同的数必为解。因为题中说每一个target只有一个解，若两个相同的数非题解的话，则出现一个target有两个解。

    时间复杂度O(N)—一次循环处理

    空间复杂度O(N)—一个等长度的HashMap

    重点⭐：先检查是否有target - x，再插入map

2.字母异位词分组mid

要点⭐⭐：字母出现的次数相同

  • 排序法：将strs数组中的str进行排序，那么异位词之间的排序应该相同，则将这些排序作为key存入HashMap，value为字母异位次的List<String>列表。

    HashMap<String, List<String>>  map = new HashMap<>();
for (String str : strs){//此句的空间复杂度  n
    char[] arrs = str.toCharArray();
    Arrays.sort(arrs);//此句的空间复杂度 klogk
    String key = new String(arrs);//此处不可用arrs.toString()
    List<String> list = map.getOrDefault(key,new ArrayList<String>());
    list.add(str);
    map.put(key,list);//得到list之后要放入Map中
}
return new ArrayList<List<String>>(map.values());

    arrs.toString()的结果是：

    stdout:
    [C@20ad9418
    [C@31cefde0
    [C@439f5b3d
    [C@1d56ce6a
    [C@5197848c
    [C@17f052a3

在这里插入图片描述

时间复杂度：O(nklogk)—n为strs的长度，k为最大str的长度

​ 对于每个字符串，需要 O(klogk) 的时间进行排序–所以准确来说为O(nklogk);

空间复杂度：O(nk)

  • 计数法：通过计算每一个str中所含有字母的个数来判断，每一个str都计算一个26位的数组用来计数。通过构建字符串key=“[字母][个数][字母][个数]”的形式来构成HashMap的key，value为字母异位次的List<String>列表。

    HashMap<String, List<String>>  map = new HashMap<>();
for(String str : strs){//此句时间复杂度 n
    char[] arrs = str.toCharArray();//此句空间复杂度 n
    int[] count = new int[26];
    for (int i = 0; i < arrs.length; i++) { 此句空间复杂度 k 时间复杂度 k
        count[arrs[i]-'a']++;
    }
    StringBuilder sb = new StringBuilder();//使用builder来构建String
    for (int i = 0; i < 26; i++) {
        if (count[i]!=0){
            sb.append((char)i+'a');   //需注意区分i(--代表字母)和count[i](--代表个数)的含义
            sb.append(count[i]);
        }
    }
    String key = sb.toString();
    List<String> list = map.getOrDefault(key, new ArrayList<String>());
    list.add(str);
    map.put(key,list);
}
return new ArrayList<List<String>>(map.values());

    时间复杂度：O(nk)

    空间复杂度：O(nk)

在这里插入图片描述

3.最长连续序列mid

解决办法是连续序列就找这个连续中最小的值（若有当前值-1的值，则跳过），找到后再去找是否存在最小值+1的值。若存在则当前长度+1，再去找再+1的值，直至不存在。若不存在则将longestLength=Math.max(currentLength,LongestLength)赋值。

HashSet<Integer> setNum = new HashSet<>();//用来去重和找有否包含
//放入Set
for (int num:nums){
    setNum.add(num);
}
/**
 * 是否含有num-1，若有则跳过。
 * 若没有着当前长度为1，再寻找num+1，若有当前长度+1。
 * 若没有则当前长度传给总长度，当前长度清零。
 */
int longestLength = 0;
for (int num : setNum){//这里遍历的是set，去重之后运算时间更快
    int currentLength = 0;
    int currentNum = num;
    if (!setNum.contains(currentNum-1)) {
        currentLength++;
        while (setNum.contains(++currentNum)){
            currentLength++;
        }
        longestLength=Math.max(longestLength,currentLength);
    }

}
return longestLength;

时间复杂度和空间复杂度都为O(n)

在这里插入图片描述

找最小值

在这里插入图片描述

4.连续零easy

双指针：办法就是右指针遍历一遍，找到所有的非零值，然后依次放在左边⭐。左边每放一个值，左指针就往右移动一个。直到右指针走到数组的末尾，此时左指针指的是0的开始第一位，将左指针所指开始到结束所有位置写上零。

int left = 0,right = 0;
//找到第一个零，从第一个0开始
//while (left<nums.length&&nums[left]!=0){//加一句判断是否越界
  //  left++;
//}
//for (right=left+1; right < nums.length; right++) {
for (right=0; right < nums.length; right++) {//右指针从零开始，查询所有的非零数，查到之后直接写道左边
    if (nums[right]!=0){//用if，若是用while的话
        nums[left++]=nums[right];//这一句的left一直++
    }
}
while (left<nums.length){//左指针之后的所有数均为零。
    nums[left++]=0;
}

在这里插入图片描述

时间复杂度：O(n)

空间复杂度：O(1)

5.盛最多水的容器mid

双指针：数组左右两边一边一个指针，计算当前面积currentArea并于最大面积比较，将较大的值赋值给largestArea。然后，比较两个指针所对应的值，移动较小的那个指针⭐，再计算面积，再赋值。

int left = 0;
int right = height.length-1;
int currentArea = 0;
int largestArea = Integer.MIN_VALUE;
while (left<right){
    currentArea=(right-left)*Math.min(height[left],height[right]);
    largestArea=Math.max(largestArea,currentArea);
    if (height[left]<=height[right]){
        left++;
    }else
        right--;
}
return largestArea;

时间复杂度：O(n)

空间复杂度：O(1)

重点是⭐：两个指针放在左右两边，然后将较小的那个往中间移动。移动较大的话，最大也不会大于当前的值。

6.三数之和mid

最常见的就是一个遍历算法，三层遍历的方法。分别选出第一个第二个和第三个。

问题：

  • 这种算法不容易避免结果重复
  • 算法的时间复杂度将达到O(N3)

但是我们可以先对数组排序，依次遍历第一个和第二个数。知道第一个和第二个数之后，由于nums[first]+nums[second]+nums[third]=0可知，针对排序后的数组，去倒序遍历第三个数。三个数不重复的情况下便有first>second>third。则第三个数只需要遍历到second，若之后还未找到满足第三个数则第二个循环结束。

Arrays.sort(nums);//排完序从小到大 空间复杂度O(nlogn)
List<List<Integer>> res  =new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
    if (i>0&&nums[i]==nums[i-1]){  //第一个数，不取与上次相同的数。重点
        continue;
    }
    int k = nums.length-1;//第三个数声明在这，即第二个数依次增大，大于上一个的数不必要再取。
    for (int j = i+1; j < nums.length; j++) {
        if (j>i+1&&nums[j]==nums[j-1]) continue；//第一个数，不取与上次相同的数。
        while (k>j&&nums[k]>-nums[i]-nums[j]）{
            k--;
        }
        if (k<=j){  //若全是大于的数，则跳出第二个数的遍历。重点
            break;
        }
        if (nums[k]==-nums[i]-nums[j]){
            List<Integer> list = new ArrayList<>();
            list.add(nums[i]);
            list.add(nums[j]);
            list.add(nums[k]);
            res.add(list);
        }
    }
}
return res;

两次去重，可保证不再有重复的结果。

第三个数声明在第二次遍历之外，当第二次遍历second时。

  • 若第三个数一直大于-nums[second]-nums[third],则second之后的数也将找不到满足条件的数。所以跳出二次遍历。
  • 若第三个数找到满足条件的了，那么第二个数继续遍历，由于是排序之后的，则下一个second一定比当前的大。所以满足条件的third一定在当前third的左边，所以third不需要重置。

在这里插入图片描述

时间复杂度：O(n2)

​ 可将second遍历和third遍历看成一次。

空间复杂度：O(nlogn)/+O(n)

7.接雨水hard

在这里插入图片描述

  • 动态规划：采用两个数组left[]和right[]来记录第i个位置的左右边界，左边界的值从左往右遍历为left[i]=max(left[i-1],height[i])。右边界的值从右往左遍历为right[height.length-1-i] = Math.max(right[height.length-i],height[height.length-1-i]);。计算i位置的存水量为Math.min(left[i],right[i])-height[i];。并且两个数组的初始值为height[0],height[n-1]。

    //左右边界
int[] left = new int[height.length];
int[] right = new int[height.length];
int v=0;
Arrays.fill(left,0);
Arrays.fill(right,0);
//确定左右边界
left[0]=height[0];
right[right.length-1]=height[height.length-1];//初始化边界很重要
for (int i = 1; i < height.length; i++) {
    left[i] = Math.max(left[i-1],height[i]);
    right[height.length-1-i]=Math.max(right[height.length-i],height[height.length-1-i]);
}
//计算ide水量=
for (int i = 0; i < height.length; i++) {
    v+=Math.min(left[i],right[i])-height[i];
}
return v;

    时间复杂度：O(n)

    空间复杂度：O(n)

  • 单调栈：采用栈的形式，维护一个递减的单调栈。保证里面可以有一个凹陷，所以栈中最少有两个值。

    • 当栈为空时，直接将当前的i压入栈。

    • 当不为空时，只要当前的height[i]>height[stack.peek()]是一个升序，就可进行判断，是否要计算或者弹出。升序最起码证明出stack.peek()较小。只需证明除了栈顶元素栈内还有元素，就可证明栈内至少有两个元素。

      • 若没有两个元素，则当前栈内+当前这个为升序，所以弹出栈内元素，保证递减。重新压入当前的i。

      • 若有两个元素，则进行计算，并且弹出top。将left作为新的top。重新压入当前的i。（这两步无论走哪一条逻辑都有弹出元素，所以在判断之前先弹出栈顶。并且之后都要压入当前的元素，所以push放在最后统一执行。）

        在这里插入图片描述

        //单调栈,递减
Stack<Integer> stack = new Stack<>();
int v = 0;
for (int i = 0; i < height.length; i++) {
    if (stack.isEmpty()){
        stack.push(i);
        continue;
    }
    while (height[i]>height[stack.peek()]) {//只要满足此条件就一直执行，计算所有以heigh[i]作为右边界的所有区间
        int top = stack.pop();//先弹出栈顶，看能否剩下一个
        if (stack.isEmpty()) {//保证不会为空,判断是否多于两个
            break;
        }
        int left = stack.peek();
        v += (i - left - 1) * (Math.min(height[i], height[left]) - height[top]);//计算i位置的存水量。
    }
    stack.push(i);
}
return v;

  • 双指针：有动态规划推导而来。可见两个边界数组均为有序的，且一个递增一个递减。那我们可以用两个常量leftMax=max(leftMax,height[left])和rightMax=max(rightMax,height[right])来表示当前left位置的左边界和当前right位置的右边界。

    • 当leftMax<rightMax时，此时当前left位置左边界固定为leftMax，而右边界又为递增的，所以left的之后的右边界将一直大于leftMax，所以决定left位置的存水量的为leftMax。计算left位置存水量：leftMax-height[left];

    • 当leftMax>=rightMax时，此时right的右边界为rightMax，此后leftMax将一直增大。rightMax将限制right位置存水量，计算right位置的存水量为：rightMax-height[right];。

      //双指针
int heightLength = height.length;
int leftMax = 0,rightMax = 0;
int v = 0;
int left = 0,right=heightLength-1;//两个指针，从左从右遍历
while ( left<=right) {//直到相遇
    leftMax=Math.max(leftMax,height[left]);
    rightMax=Math.max(rightMax,height[right]);
    //left的村水量
    if (leftMax<rightMax){
        v+=leftMax-height[left];
        left++;//计算完left之后，计算下一个left
    }else {
        v+=rightMax-height[right];
        right--;
    }
}
return v;

      时间复杂度：O(n)

      空间复杂度：O(1)

    在这里插入图片描述

8.无重复数组的最长子串mid

采用滑动窗口的方法，使用HashSet结构记录当前窗口内所包含的不重复的子串。判断set中是否包含right的位置的字符。如果包含则移除set中arr[i],并且i++滑动窗口左边界向右移。如果不包含则将arr[right]加入set中，并扩展右边界right++，记录当前最长的子串。

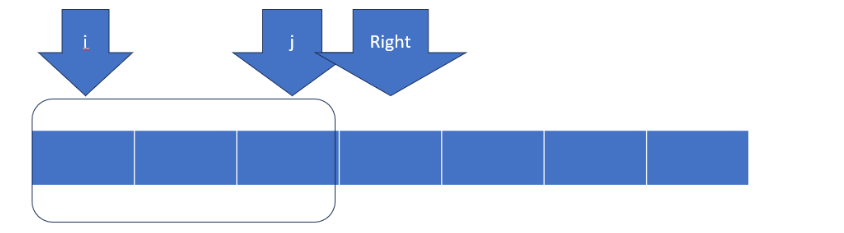
在这里插入图片描述

//选定一个开始，一个结尾。记录当前的子串长度
int longest = 0,current = 0;
int right = 0;
int sLength = s.length();
char[] arr = s.toCharArray();
Set<Character> set  = new HashSet<>();//去重set
for (int i = 0; i < sLength; i++) {
    while (right<sLength&&(set.isEmpty()||!set.contains(arr[right]))){//若right没到结尾，并且set为空（窗口为空）或者set不包含right位置的字符。则加入窗口，更新最大值。
        set.add(arr[right++]);
        current++;
        longest = Math.max(longest,current);
    }
    set.remove(arr[i]);//若有重复的则删除左边界，更新当前长度。
    current--;
}
return longest;

时间复杂度：O(n)

空间复杂度：O(n)

9.找到所有字符串中的字母异位词mid

采用计数的方式，pCount统计p中的每个字符个数。而s中则采用定长的滑动窗口。初始化之后，若pCount与sCount相同Arrays.equals(pCount,sCount)则记录当前的字符的下标。

在这里插入图片描述

public List<Integer> findAnagrams(String s, String p) {
    if (p.length()>s.length()){//判断是否合理
        return new ArrayList<>();//返回空List
    }
    //计数
    int[] countp = new int[26];
    int[] countstr = new int[26];//子串的计数
    List<Integer> list = new ArrayList<>();
    //p
    for (int i = 0; i < p.length(); i++) {//分别记录plength长度内字符出现的字数
        countp[p.charAt(i)-'a']++;
        countstr[s.charAt(i)-'a']++;//先记录0~plength-1内的
    }
    //
    if (Arrays.equals(countp,countstr)){//判断0~plength-1内有没有，有的话记录0
        list.add(0);
    }
    //
    for (int i = 0; i < s.length() - p.length(); i++) {//注意i的取值范围
        countstr[s.charAt(i)-'a']--;//去除滑动窗口左边的
        countstr[s.charAt(i+p.length())-'a']++;//加上滑动窗口右边的，因为要定长
        if (Arrays.equals(countp,countstr)){//走一下判断一下
            list.add(i+1);
        }
    }
    return list;
}

时间复杂度：O(n)??

p[p.charAt(i)-‘a’]++;
countstr[s.charAt(i)-‘a’]++;//先记录0~plength-1内的
}
//
if (Arrays.equals(countp,countstr)){//判断0~plength-1内有没有，有的话记录0
list.add(0);
}
//
for (int i = 0; i < s.length() - p.length(); i++) {//注意i的取值范围
countstr[s.charAt(i)-‘a’]–;//去除滑动窗口左边的
countstr[s.charAt(i+p.length())-‘a’]++;//加上滑动窗口右边的，因为要定长
if (Arrays.equals(countp,countstr)){//走一下判断一下
list.add(i+1);
}
}
return list;
}


> 时间复杂度：O(n)??
>
> 空间复杂度：O(1)??

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2396488.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Postman 发送 SOAP 请求步骤 归档

Postman 发送 SOAP 请求步骤 归档

0.来源 https://apifox.com/apiskills/sending-soap-requests-with-postman/?utm_sourceopr&utm_mediuma2bobzhang&utm_contentpostman 再加上自己一点实践经验 1. 创建一个新的POST请求 postman 创建一个post请求, 请求url 怎么来的可以看第三步 2. post请求设…
阅读更多...
Python Day39 学习（复习日志Day4）

Python Day39 学习（复习日志Day4）

复习Day4日志内容 浙大疏锦行 补充: 关于“类”和“类的实例”的通俗易懂的例子 补充&#xff1a;如何判断是用“众数”还是“中位数”填补空缺值&#xff1f; 今日复习了日志Day4的内容&#xff0c;感觉还是得在纸上写一写印象更深刻&#xff0c;接下来几日都采取“纸质化复…
阅读更多...
[Python] Python自动化：PyAutoGUI的基本操作

[Python] Python自动化：PyAutoGUI的基本操作

初次学习&#xff0c;如有错误还请指正 目录 PyAutoGUI介绍 PyAutoGUI安装 鼠标相关操作 鼠标移动 鼠标偏移 获取屏幕分辨率 获取鼠标位置 案例&#xff1a;实时获取鼠标位置 鼠标点击 左键单击 点击次数 多次有时间间隔的点击 右键/中键点击 移动时间 总结 鼠…
阅读更多...
应急响应靶机-web2-知攻善防实验室

应急响应靶机-web2-知攻善防实验室

题目&#xff1a; 前景需要&#xff1a;小李在某单位驻场值守&#xff0c;深夜12点&#xff0c;甲方已经回家了&#xff0c;小李刚偷偷摸鱼后&#xff0c;发现安全设备有告警&#xff0c;于是立刻停掉了机器开始排查。 这是他的服务器系统&#xff0c;请你找出以下内容&#…
阅读更多...
comfyui利用 SkyReels-V2直接生成长视频本地部署问题总结 1

comfyui利用 SkyReels-V2直接生成长视频本地部署问题总结 1

在通过桌面版comfyUI 安装ComfyUI-WanVideoWrapper 进行SkyReels-V2 生成长视频的过程中&#xff0c;出现了&#xff0c;很多错误。 总结一下&#xff0c;让大家少走点弯路 下面是基于搜索结果的 ComfyUI 本地部署 SkyReels-V2 实现长视频生成的完整指南&#xff0c;涵盖环境配…
阅读更多...
YOLOv8 实战指南：如何实现视频区域内的目标统计与计数

YOLOv8 实战指南：如何实现视频区域内的目标统计与计数

文章目录 YOLOv8改进 | 进阶实战篇&#xff1a;利用YOLOv8进行视频划定区域目标统计计数1. 引言2. YOLOv8基础回顾2.1 YOLOv8架构概述2.2 YOLOv8的安装与基本使用 3. 视频划定区域目标统计的实现3.1 核心思路3.2 完整实现代码 4. 代码深度解析4.1 关键组件分析4.2 性能优化技巧…
阅读更多...
matlab实现VMD去噪、SVD去噪，源代码详解

matlab实现VMD去噪、SVD去噪，源代码详解

为了更好的利用MATLAB自带的vmd、svd函数&#xff0c;本期作者将详细讲解一下MATLAB自带的这两个分解函数如何使用&#xff0c;以及如何画漂亮的模态分解图。 VMD函数用法详解 首先给出官方vmd函数的调用格式。 [imf,residual,info] vmd(x) 函数的输入&#xff1a; 这里的x是待…
阅读更多...
SQLite软件架构与实现源代码浅析

SQLite软件架构与实现源代码浅析

概述 SQLite 是一个用 C 语言编写的库&#xff0c;它成功打造出了一款小型、快速、独立、具备高可靠性且功能完备的 SQL 数据库引擎。本文档将为您简要介绍其架构、关键组件及其协同运作模式。 SQLite 显著特点之一是无服务器架构。不同于常规数据库&#xff0c;它并非以单独进…
阅读更多...
JAVA实战开源项目：精简博客系统 (Vue+SpringBoot) 附源码

JAVA实战开源项目：精简博客系统 (Vue+SpringBoot) 附源码

本文项目编号 T 215 &#xff0c;文末自助获取源码 \color{red}{T215&#xff0c;文末自助获取源码} T215&#xff0c;文末自助获取源码 目录 一、系统介绍二、数据库设计三、配套教程3.1 启动教程3.2 讲解视频3.3 二次开发教程 四、功能截图五、文案资料5.1 选题背景5.2 国内…
阅读更多...
通过openpyxl在excel中插入散点图

通过openpyxl在excel中插入散点图

实现代码 # -*- coding: utf-8 -*- """ Created on Sat May 31 23:30:12 2025author: anyone """from openpyxl import load_workbook from openpyxl.chart import ScatterChart, Reference, Series from openpyxl.chart.series import SeriesL…
阅读更多...
基于cornerstone3D的dicom影像浏览器 第二十五章 自定义VR调窗工具

基于cornerstone3D的dicom影像浏览器 第二十五章 自定义VR调窗工具

文章目录 前言一、三维调窗原理二、自定义三维调窗工具三、调用流程1. 修改mprvr.js2. 修改DispalyerArea3D.vue3. view3d.vue4. Toolbar3D.vue 总结 前言 从cornerstoneTools BaseTool派生VolumeShiftColorTool&#xff0c;实现鼠标键按下并移动时&#xff0c;对3D窗口的pres…
阅读更多...
经典面试题：一文了解常见的缓存问题

经典面试题：一文了解常见的缓存问题

在面试过程中&#xff0c;面试官的桌子上摆放着很多高频的面试题&#xff0c;能否顺利回答决定了你面试通过的概率。其中缓存问题就是其中的一份&#xff0c;可以说掌握缓存问题及解决方法是面试前必须准备的内容。那么缓存有什么典型的问题&#xff0c;出现的原因是什么&#…
阅读更多...
GC1267F：单相全波风扇电机预驱动芯片解析

GC1267F：单相全波风扇电机预驱动芯片解析

在现代电子设备中&#xff0c;风扇电机的驱动控制是散热系统的关键组成部分。GC1267F 是一款由浙江新麦科技有限公司生产的单相全波风扇电机预驱动芯片&#xff0c;适用于需要大风量和大电流的服务器以及消费类电器风扇电机驱动。 芯片特性 GC1267F 支持外部 PWM 信号的变速功…
阅读更多...
Linux --进程状态

Linux --进程状态

目录 进程状态(宏观) Linux进程状态 进程状态的查看 进程状态(宏观) 为了了解Linux的进程状态&#xff0c;首先我们得了解进程状态&#xff0c;因为不仅仅是在Linux下有进程状态&#xff0c;macos和windows下都有进程状态&#xff0c;这里先解释的是一个宏观概念下的&#xff…
阅读更多...
智能手机上用Termux安装php+Nginx

智能手机上用Termux安装php+Nginx

Termux的官方网站&#xff1a;Termux | The main termux site and help pages. 以下是在 Termux 上安装和配置 PHP Nginx 的完整流程总结&#xff0c;包含关键步骤和命令&#xff1a; 一、安装依赖 pkg update && pkg upgrade # 更新包列表和系统pkg install nginx p…
阅读更多...
Visual Studio 调试中 PDB 与图像不匹配

Visual Studio 调试中 PDB 与图像不匹配

Visual Studio 调试中 PDB 与图像不匹配 在使用 Visual Studio 进行本地或远程调试时&#xff0c;很多开发者会遇到 PDB 加载失败、符号不匹配的问题&#xff0c;甚至程序进程未退出&#xff0c;导致 .exe 文件无法成功覆盖。本文详细解析了从后台进程清理、构建产物验证、模块…
阅读更多...
设计模式——策略设计模式（行为型）

设计模式——策略设计模式（行为型）

摘要 策略设计模式是一种行为型设计模式&#xff0c;它定义了一系列算法并将每个算法封装起来&#xff0c;使它们可以相互替换。该模式让算法的变化独立于使用算法的客户&#xff0c;从而使得算法可以灵活地切换和扩展。其主要角色包括策略接口、具体策略类和环境类。策略模式…
阅读更多...
保持本地 Git 项目副本与远程仓库完全同步

保持本地 Git 项目副本与远程仓库完全同步

核心目标&#xff1a; 保持本地 Git 项目副本与 GitHub 远程仓库完全同步。 关键方法&#xff1a; 定期执行 git pull 命令。 操作步骤&#xff1a; 进入项目目录&#xff1a; 在终端/命令行中&#xff0c;使用 cd 命令切换到你的项目文件夹。执行拉取命令&#xff1a; 运行…
阅读更多...
设计模式——模版方法设计模式（行为型）

设计模式——模版方法设计模式（行为型）

摘要 模版方法设计模式是一种行为型设计模式&#xff0c;定义了算法的步骤顺序和整体结构&#xff0c;将某些步骤的具体实现延迟到子类中。它通过抽象类定义模板方法&#xff0c;子类实现抽象步骤&#xff0c;实现代码复用和算法流程控制。该模式适用于有固定流程但部分步骤可…
阅读更多...
Deepin 20.9社区版安装Docker

Deepin 20.9社区版安装Docker

个人博客地址&#xff1a;Deepin 20.9社区版安装Docker | 一张假钞的真实世界 注意事项 Deepin 20.9 社区版安装 Docker 需要注意两点&#xff1a; 因为某些原因&#xff0c;Docker 官方源基本不可用&#xff0c;所以需要使用镜像源进行安装。当然也可以用安装包直接安装&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023