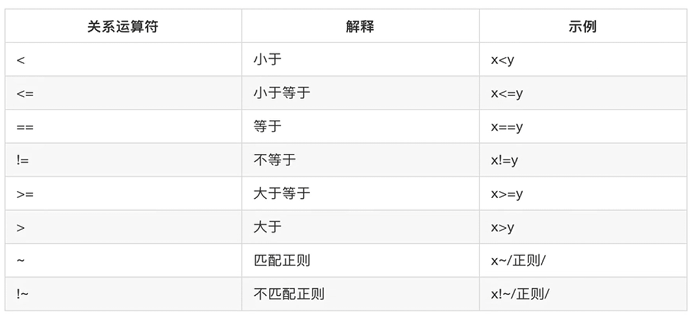
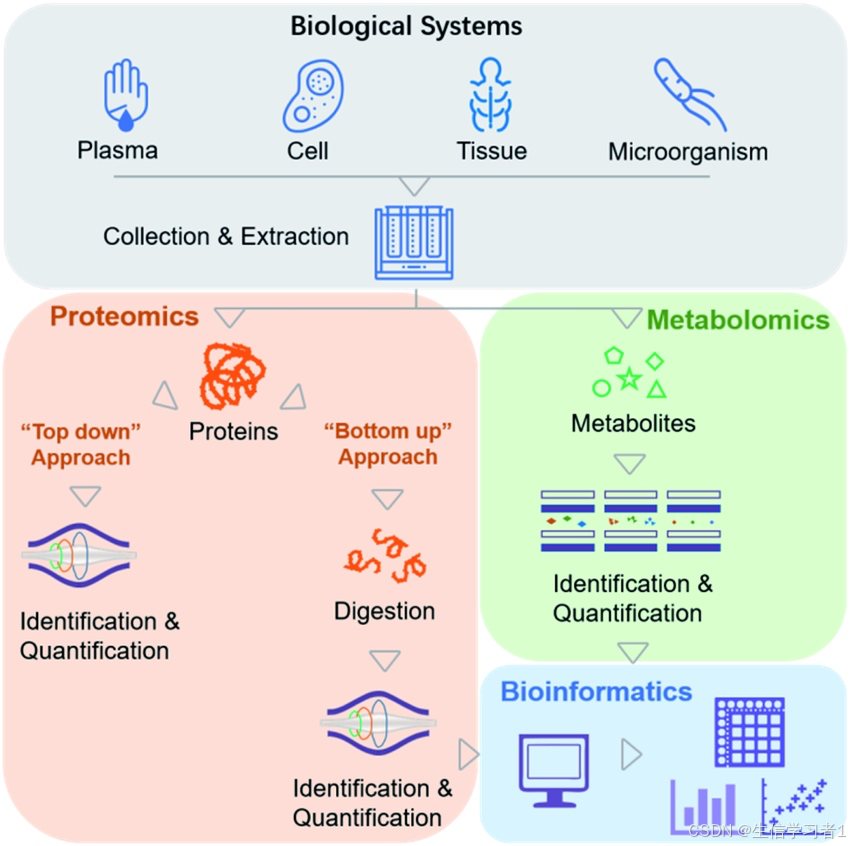
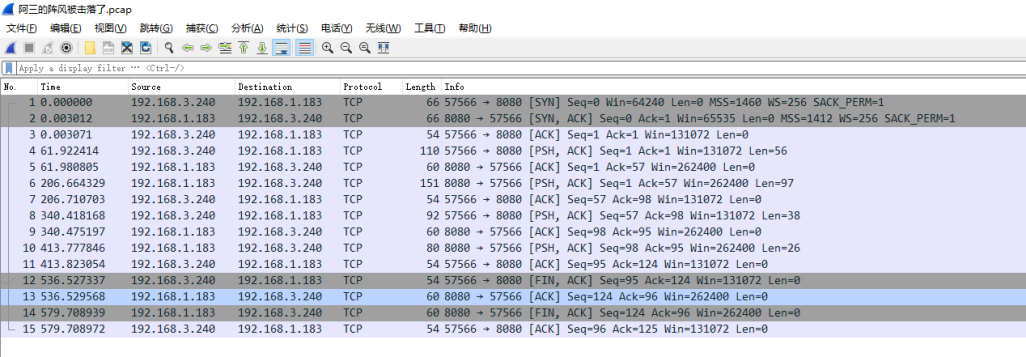
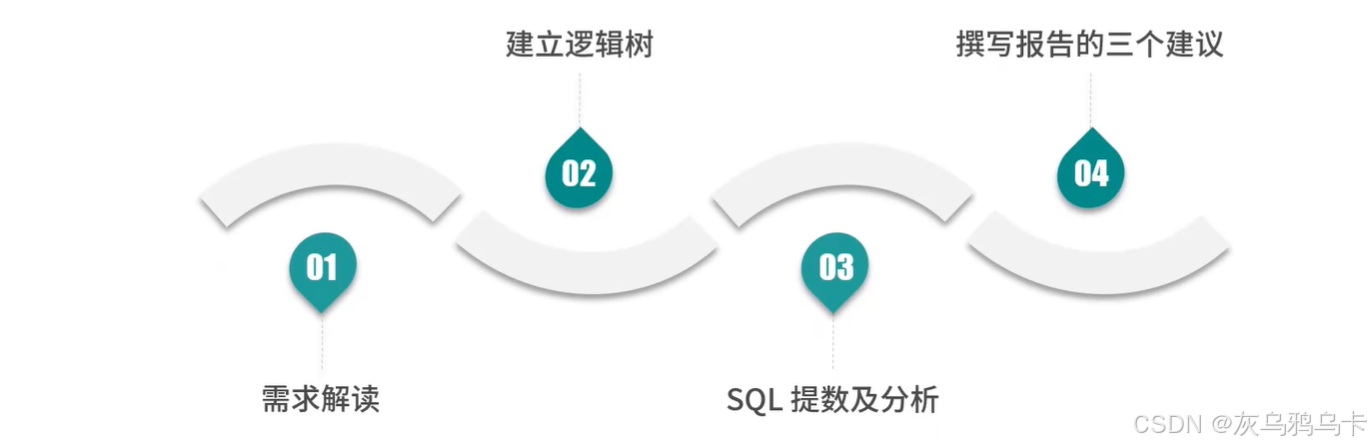
设总体 X ∼ N ( μ , σ 2 ) X \sim N(\mu, \sigma^2) X∼N(μ,σ2),其中 μ \mu μ 和 σ 2 \sigma^2 σ2 是未知参数,取样本观测值为 x 1 , x 2 , ⋯ , x n x_1, x_2, \cdots, x_n x1,x2,⋯,xn,求参数 μ \mu μ 和 σ 2 \sigma^2 σ2 的最大似然估计。
解
总体
X
X
X 的概率密度函数为
f
(
x
;
μ
,
σ
2
)
=
1
2
π
σ
e
−
(
x
i
−
μ
)
2
2
σ
2
(
−
∞
<
x
<
+
∞
)
,
f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x_i - \mu)^2}{2\sigma^2}} \quad (-\infty < x < +\infty),
f(x;μ,σ2)=2πσ1e−2σ2(xi−μ)2(−∞<x<+∞),
则似然函数为
L
(
μ
,
σ
2
)
=
∏
i
=
1
n
1
2
π
σ
e
−
(
x
i
−
μ
)
2
2
σ
2
=
(
2
π
σ
2
)
−
n
2
e
−
1
2
σ
2
∑
i
=
1
n
(
x
i
−
μ
)
2
,
L(\mu, \sigma^2) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x_i - \mu)^2}{2\sigma^2}} = (2\pi\sigma^2)^{-\frac{n}{2}} e^{-\frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2},
L(μ,σ2)=i=1∏n2πσ1e−2σ2(xi−μ)2=(2πσ2)−2ne−2σ21∑i=1n(xi−μ)2,
取对数,得对数似然函数
ln
L
(
μ
,
σ
2
)
=
−
n
2
ln
2
π
−
n
2
ln
σ
2
−
1
2
σ
2
∑
i
=
1
n
(
x
i
−
μ
)
2
,
\ln L(\mu, \sigma^2) = -\frac{n}{2} \ln 2\pi - \frac{n}{2} \ln \sigma^2 - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2,
lnL(μ,σ2)=−2nln2π−2nlnσ2−2σ21i=1∑n(xi−μ)2,
关于
μ
\mu
μ 和
σ
2
\sigma^2
σ2 分别求偏导,得似然方程组
{
∂
ln
L
(
μ
,
σ
2
)
∂
μ
=
1
σ
2
∑
i
=
1
n
(
x
i
−
μ
)
=
0
,
∂
ln
L
(
μ
,
σ
2
)
∂
σ
2
=
−
n
2
σ
2
+
1
2
σ
4
∑
i
=
1
n
(
x
i
−
μ
)
2
=
0.
\begin{cases} \frac{\partial \ln L(\mu, \sigma^2)}{\partial \mu} = \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \mu) = 0, \\ \frac{\partial \ln L(\mu, \sigma^2)}{\partial \sigma^2} = -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4} \sum_{i=1}^n (x_i - \mu)^2 = 0. \end{cases}
{∂μ∂lnL(μ,σ2)=σ21∑i=1n(xi−μ)=0,∂σ2∂lnL(μ,σ2)=−2σ2n+2σ41∑i=1n(xi−μ)2=0.
由此解得
μ
\mu
μ 及
σ
2
\sigma^2
σ2 的最大似然估计值分别为
{
μ
~
=
1
n
∑
i
=
1
n
x
i
=
x
ˉ
,
σ
2
~
=
1
n
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
,
\begin{cases} \tilde{\mu} = \frac{1}{n} \sum_{i=1}^n x_i = \bar{x}, \\ \tilde{\sigma^2} = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2, \end{cases}
{μ~=n1∑i=1nxi=xˉ,σ2~=n1∑i=1n(xi−xˉ)2,
最大似然估计量分别为
{
μ
~
=
1
n
∑
i
=
1
n
X
i
=
X
ˉ
,
σ
2
~
=
1
n
∑
i
=
1
n
(
X
i
−
X
ˉ
)
2
.
\begin{cases} \tilde{\mu} = \frac{1}{n} \sum_{i=1}^n X_i = \bar{X}, \\ \tilde{\sigma^2} = \frac{1}{n} \sum_{i=1}^n (X_i - \bar{X})^2. \end{cases}
{μ~=n1∑i=1nXi=Xˉ,σ2~=n1∑i=1n(Xi−Xˉ)2.
从例可以看到,正态总体参数的最大似然估计与矩估计是相同的。




![[嵌入式实验]实验四:串口打印电压及温度](https://i-blog.csdnimg.cn/direct/447a807c000f4538aa4f05dd4172c828.png)