【基础算法】高精度（加、减、乘、除）

news2025/6/2 12:12:19

文章目录

  • 什么是高精度
  • 1. 高精度加法
    • 解题思路
    • 代码实现
  • 2. 高精度减法
    • 解题思路
    • 代码实现
  • 3. 高精度乘法
    • 解题思路
    • 代码实现
  • 4. 高精度除法 (高精度 / 低精度)
    • 解题思路
    • 代码实现

什么是高精度

我们平时使用加减乘除的时候都是直接使用 + - * / 这些符号，前提是进行运算的数字在一定的范围之内。一旦这个数字非常大的时候，比如 10 10086 10^{10086} 1010086 这个样一个天文数字，普通的 int、long long 这些类型根本容不下它，像用它进行运算就更不可能了，所以这个时候我们就需要用到高精度算法来计算加减乘除。

高精度算法的核心有两步：

  1. 先用字符串读入这个数，然后用数组逆序存储该数的每⼀位；

  2. 利用数组，模拟小学就学过的加减乘除竖式运算过程。

1. 高精度加法

【题目链接】

P1601 A+B Problem（高精） - 洛谷

【题目描述】

高精度加法，相当于 a+b problem，不用考虑负数。

【输入格式】

分两行输入。 a , b ≤ 10 500 a,b \leq 10^{500} a,b≤10500。

【输出格式】

输出只有一行，代表 a + b a+b a+b 的值。

【示例一】

输入

1
1

输出

2

【示例二】

输入

1001
9099

输出

10100

【说明/提示】

20 % 20\% 20% 的测试数据， 0 ≤ a , b ≤ 10 9 0\le a,b \le10^9 0≤a,b≤109；

40 % 40\% 40% 的测试数据， 0 ≤ a , b ≤ 10 18 0\le a,b \le10^{18} 0≤a,b≤1018。

解题思路

  1. 先用字符串读入这个数，然后用数组逆序存储该数的每⼀位

我们可以在全局上设置三个数组 a[], b[], c[]，分别用于存储加法运算的左操作数、右操作数以及左后的结果的每一位（逆序）。比如 456 + 789 = 1245 456 + 789 = 1245 456+789=1245，对应 a[] = {6, 5, 4}, b = {9, 8, 7}, c = {5, 4, 2, 1}。同时，设置三个变量 la, lb, lc 用于记录数字的长度。

const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;

为什么要逆序？这是因为我们在人为计算竖式的时候是按照从个位到最高位去计算的，相当于逆序计算。当我们逆序存储后之后在模拟竖式计算的过程中就可以顺序遍历数组进行操作。

请添加图片描述

有了这几个变量之后就可以存储数字了，这个过程中，字符串的最后一位应存储在数组的第一位，以此类推。注意字符串中的每一位存储的是字符，而数组中存储的是数，所以在搬运各个位的时候要减去 '0' 转化成对应的数字。

string x, y;
cin >> x >> y;
la = x.size(), lb = y.size(), lc = max(la, lb); // 这里先暂时写成max(la, lb)
for(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0';
for(int i = 0; i < lb; ++i) b[lb - 1 - i] = y[i] - '0';
  1. 利用数组，模拟小学就学过的加减乘除竖式运算过程

用循环遍历数组，填写 c[] 中的每一位。

for(int i = 0; i < lc; ++i)
{
    c[i] += a[i] + b[i];  // 对应位相加，再加上进位(+=实际就是加上进位)
    c[i + 1] = c[i] / 10;  // 进到下一位去
    c[i] %= 10;  // 当前位对应的数
}

代码实现

#include<iostream>

using namespace std;

const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;

// 高精度加法
void add(int c[], int a[], int b[])
{
    // 模拟竖式运算
    for(int i = 0; i < lc; ++i)
    {
        c[i] += a[i] + b[i];  // 对应位相加，再加上进位
        c[i + 1] = c[i] / 10;  // 处理进位
        c[i] %= 10;  // 当前位对应的数
    }

    // 如果最后一位进位了，那么c的长度+1
    if(c[lc]) ++lc;
}

int main()
{
    string x, y;
    cin >> x >> y;

    // 拆分每一位数字，并逆序放在数组中
    la = x.size(), lb = y.size(), lc = max(la, lb);
    for(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0';
    for(int i = 0; i < lb; ++i) b[lb - 1 - i] = y[i] - '0';

    // 高精度加法：c = a + b
    add(c, a, b);

    // 逆序输出
    for(int i = lc - 1; i >= 0; --i) cout << c[i];
    
    return 0;
}

2. 高精度减法

【题目链接】

P2142 高精度减法 - 洛谷

【题目描述】

高精度减法。

【输入格式】

两个整数 a , b a,b a,b（第二个可能比第一个大）。

【输出格式】

结果（是负数要输出负号）。

【示例一】

输入

2
1

输出

1

【说明/提示】

  • 20 % 20\% 20% 数据 a , b a,b a,b 在 long long 范围内；
  • 100 % 100\% 100% 数据 0 < a , b ≤ 10 10086 0<a,b\le 10^{10086} 0<a,b≤1010086。

解题思路

和高精度加法很类似，只不过这里要处理两个细节

  1. 结果可能为负数

当 x - y 的 x 比 y 小的时候，结果为负数，我们可以交换 x 和 y 的值然后在计算的结果后加上 - 即可。

而由于 x 和 y 是字符串，所以判断 x 和 y 的 “大小” 时需要考虑两个点：

  • 字符串长度长的对应的数一定更大。

  • 如果字符串长度一样，那么从前往后比较每一位的字典序（直接用 < 或 > 比较即可）。

  1. 可能出现前导 0

我们最终输出的数的位数由 lc 决定，如果我们让 lc 的值等于 max(la, lb) 而不做处理的话下面的运算结果就为 078 而不是 78。

请添加图片描述

所以这个时候我们就需要更新 lc，可以考虑从 c[] 数组的 c[lc - 1] 位置开始往前遍历，直到遇到第一个不是 0 的位置或者lc == 0 的时候结束，在这个过程中不断让 lc 减一。

while(lc > 1 && c[lc - 1] == 0) --lc;  // 处理前导0

注意不能是 lc > 0，因为有可能两数相等相减的最终结果为 0。

代码实现

#include<iostream>

using namespace std;

const int N = 1e6 + 10;

int a[N], b[N], c[N];
int la, lb, lc;

// 高精度减法
void sub(int c[], int a[], int b[])
{
    // 模拟竖式运算
    for(int i = 0; i < lc; ++i)
    {
        c[i] += a[i] - b[i];  // 对应位相减，并处理借位
        if(c[i] < 0)
        {
            c[i + 1] -= 1;  // 借位
            c[i] += 10;
        }
    }
    
    while(lc > 1 && c[lc - 1] == 0) --lc;  // 处理前导0
}

int main()
{
    string x, y;
    cin >> x >> y;

    // 计算 x - y
    // 如果 x 对应的数比 y 对应的数小，那么交换二者，并在结果前加上负号
    if(x.size() < y.size()
    || (x.size() == y.size() && x < y))
    {
        cout << '-';
        swap(x, y);
    }

    // 拆分每一位数字，并逆序放在数组中
    la = x.size(), lb = y.size(), lc = max(la, lb);
    for(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0';
    for(int i = 0; i < lb; ++i) b[lb - 1 - i] = y[i] - '0';

    sub(c, a, b);
    
    for(int i = lc - 1; i >= 0; --i) cout << c[i];
    
    return 0;
}

3. 高精度乘法

【题目链接】

P1303 A*B Problem - 洛谷

【题目描述】

给出两个非负整数，求它们的乘积。

【输入格式】

输入共两行，每行一个非负整数。

【输出格式】

输出一个非负整数表示乘积。

【示例一】

输入

1 
2

输出

2

【说明/提示】

每个非负整数不超过 10 2000 10^{2000} 102000。

解题思路

乘法也可以模拟普通竖式运算过程，但是这样会频繁地处理进位，因为我们也可以采取另一种方式：无进位相乘，相加到对应位上，最后再统一处理进位。

请添加图片描述

通过下标的对应关系我们可以发现， a[] 的第 i 个位置的数与 b[] 的第 j 个位置的数相乘恰好就加在 c[] 的第 i + j 位置上。

for(int i = 0; i < la; ++i)
    for(int j = 0; j < lb; ++j)
        c[i + j] += a[i] * b[j];

当我们相加之后，再来处理进位。

for(int i = 0; i < lc; ++i)
{
    c[i + 1] += c[i] / 10;
    c[i] %= 10;
}

同样可能出现前导 0 的问题，比如 10000 * 0，于是我们采用相同的方法处理：

while(lc > 1 && c[lc - 1] == 0) --lc;

代码实现

#include<iostream>

using namespace std;

const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;

void mul(int c[], int a[], int b[])
{
    // 无进位相乘，相加到对应位上
    for(int i = 0; i < la; ++i)
    	for(int j = 0; j < lb; ++j)
        	c[i + j] += a[i] * b[j];
    
    // 处理进位
    for(int i = 0; i < lc; ++i)
    {
        c[i + 1] += c[i] / 10;
        c[i] %= 10;
    }
	
    // 处理前导0
    while(lc > 1 && c[lc - 1] == 0) --lc;
}

int main()
{
    string x, y;
    cin >> x >> y;

    la = x.size(), lb = y.size(), lc = la + lb;  // 两数相乘长度最多不超过la + lb
    for(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0';
    for(int i = 0; i < lb; ++i) b[lb - 1 - i] = y[i] - '0';

    mul(c, a, b);

    for(int i = lc - 1; i >= 0; --i) cout << c[i];

    return 0;
}

4. 高精度除法 (高精度 / 低精度)

【题目链接】

P1480 A/B Problem - 洛谷

【题目描述】

输入两个整数 a , b a,b a,b，输出它们的商。

【输入格式】

两行，第一行是被除数，第二行是除数。

【输出格式】

一行，商的整数部分。

【示例一】

输入

10
2

输出

5

【说明/提示】

0 ≤ a ≤ 10 5000 0\le a\le 10^{5000} 0≤a≤105000， 1 ≤ b ≤ 10 9 1\le b\le 10^9 1≤b≤109。

解题思路

由于遇到较多的一般是高精度 / 低精度，所以这里就只讲这种情况。

模拟除法的竖式运算时，实际上会用到多次除法运算，我们可以用一个变量 t 来记录每次的被除数，除出来的商放在 c[] 中的对应位置，然后更新 t，总共除 la 次。最后处理前导 0 即可。

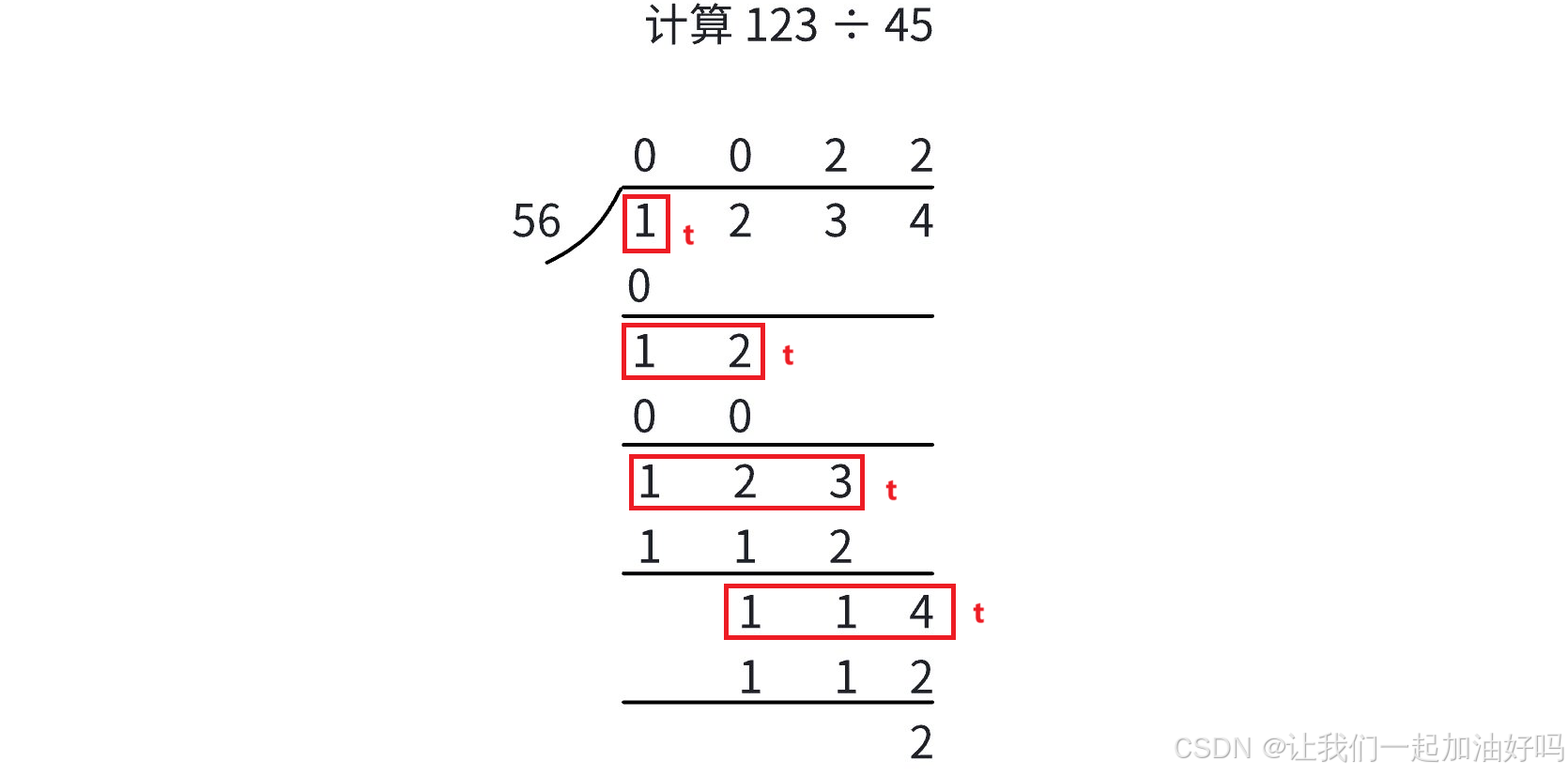
请添加图片描述

注意数据范围，b 最大是 10 9 10^9 109，而 t 可能是 b 的几倍，所以 t 可以用 long long 来存储。

代码实现

#include<iostream>

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;
int a[N], b, c[N];
int la, lc;

// 高精度除法(高精度 / 低精度)
void div(int c[], int a[], int b)
{
    LL t = 0;
    for(int i = la - 1; i >= 0; --i)
    {
        t = t * 10 + a[i];  // 计算当前的被除数
        c[i] = t / b;
        t %= b;
    }

    // 处理前导0
    while(lc > 1 && c[lc - 1] == 0) --lc;
}

int main()
{
    string x; cin >> x;
    int b; cin >> b;

    la = x.size(), lc = la;
    for(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0'; 

    div(c, a, b);

    for(int i = lc - 1; i >= 0; --i) cout << c[i];

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2394314.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Windows最快速打开各项系统设置大全

Windows最快速打开各项系统设置大全

目录 一、应用背景 二、设置项打开方法 2.1 方法一界面查找&#xff08;最慢&#xff09; 2.2 方法二cmd命令&#xff08;慢&#xff09; 2.3 方法三快捷键&#xff08;快&#xff09; 2.4 方法四搜索栏&#xff08;快&#xff09; 2.5 方法五任务栏&#xff08;最快&am…
阅读更多...
嵌入式编译工具链熟悉与游戏移植

嵌入式编译工具链熟悉与游戏移植

在自己的虚拟机Ubuntu系统下&#xff0c;逐步编译 mininim源码(波斯王子重制开源版&#xff09; 指令流程 sudo apt-get remove liballegro5-dev liballegro-image5-dev \liballegro-audio5-dev liballegro-acodec5-dev liballegro-dialog5-dev sudo apt-get install automak…
阅读更多...
DeepSeek-R1-0528，官方的端午节特别献礼

DeepSeek-R1-0528，官方的端午节特别献礼

DeepSeek&#xff1a;端午安康&#xff01;刻在国人骨子里的浪漫 2025 年 05 月 28 日 | DeepSeek 端午特别献礼 当粽叶飘香时&#xff0c;DeepSeek 悄然带来一份节日惊喜 版本号 DeepSeek-R1-0528 正式上线 官方赋予它的灵魂是&#xff1a; 思考更深 推理更强 用户通过官网…
阅读更多...
001 flutter学习的注意事项及前期准备

001 flutter学习的注意事项及前期准备

在学习flutter之前&#xff0c;还需要进行一些初始的配置&#xff0c;然后才可以学习flutter 1.安装flutter 国内官网&#xff1a;https://flutter.cn​​​​​​ 国际官网&#xff1a;https://flutter.dev 安装完成后&#xff0c;按照官网上面的操作步骤进行配置&#xf…
阅读更多...
CS144 - Lecture 1 记录

CS144 - Lecture 1 记录

CS144 - Lecture 1 由于没讲义&#xff0c;全看课了&#xff0c;系统性的总结有点难&#xff0c;记一些有趣的东西吧。 数据链路和网络层的传输 我们可以看见&#xff0c;对于发送方&#xff0c;我们的数据链路层为我们的网络层提供服务&#xff0c;在经过路由的时候&#xf…
阅读更多...
【数据结构】——二叉树--链式结构

【数据结构】——二叉树--链式结构

一、实现链式结构二叉树 二叉树的链式结构&#xff0c;那么从名字上我们就知道我们这个二叉树的底层是使用链表来实现的&#xff0c;前面我们的二叉树是通过数组来实现的&#xff0c;那么在其是完全二叉树的情况下&#xff0c;此时我们使用数组来实现就会使得其空间浪费较少&a…
阅读更多...
充电便捷，新能源汽车移动充电服务如何预约充电

充电便捷，新能源汽车移动充电服务如何预约充电

随着新能源汽车的普及&#xff0c;充电便捷性成为影响用户体验的关键因素之一。传统的固定充电桩受限于地理位置和数量&#xff0c;难以完全满足用户需求&#xff0c;而移动充电服务的出现&#xff0c;为车主提供了更加灵活的补能方式。通过手机APP、小程序或在线平台&#xff…
阅读更多...
基于 Chrome 浏览器扩展的Chroma简易图形化界面

基于 Chrome 浏览器扩展的Chroma简易图形化界面

简介 ChromaDB Manager 是基于 Chrome 浏览器扩展的一款 ChromaDB&#xff08;一个流行的向量数据库&#xff09;的数据查询工具。提供了一个用户友好的界面&#xff0c;可以直接从浏览器连接到本地 ChromaDB 实例、查看集合信息和分片数据。本工具特别适合开发人员快速查看和…
阅读更多...
IM系统的负载均衡

IM系统的负载均衡

1.IM场景的负载均衡 2.方案总览 SDK层想要连接一个TCP网关或者WebSocket网关的方案 SDK单地址：在SDK中写死某个网关的IP或者域名，缺点是更换地址需要重新打包SDK SDK多地址：防止某一个地址嗝屁了写上多个地址用足保持高可用 暴露接口给客户端：SDK层访问接口动态获得地址 注…
阅读更多...
使用 Zabbix 监控 MySQL 存储空间和性能指标的完整实践指南

使用 Zabbix 监控 MySQL 存储空间和性能指标的完整实践指南

目录 引言 一、最终目标支持功能 二、监控方案设计 2.1 技术选型 2.2 设计思路 三、实现步骤 3.1 准备工作 3.11 创建 MySQL 监控账号 3.12 配置 .my.cnf 文件 3.2 编写统一脚本 3.3 配置 Zabbix Agent UserParameter 3.4 Zabbix 前端配置建议 四、总结 引言 MySQL …
阅读更多...
【技能拾遗】——家庭宽带单线复用布线与配置（移动2025版）

【技能拾遗】——家庭宽带单线复用布线与配置（移动2025版）

&#x1f4d6; 前言&#xff1a;在家庭网络拓扑中&#xff0c;客厅到弱电箱只预埋了一根网线&#xff0c;由于已将广电的有线电视取消并改用IPTV。现在需要解决在客厅布置路由器和观看IPTV问题&#xff0c;这里就用到单线复用技术。 目录 &#x1f552; 1. 拓扑规划&#x1f55…
阅读更多...
异步日志监控：FastAPI与MongoDB的高效整合之道

异步日志监控：FastAPI与MongoDB的高效整合之道

title: 异步日志监控：FastAPI与MongoDB的高效整合之道 date: 2025/05/27 17:49:39 updated: 2025/05/27 17:49:39 author: cmdragon excerpt: FastAPI与MongoDB整合实现日志监控系统的实战指南。首先配置MongoDB异步连接，定义日志数据模型。核心功能包括日志写入接口、聚合…
阅读更多...
在 Android 上备份短信：保护您的对话

在 Android 上备份短信：保护您的对话

尽管我们的Android手机有足够的存储空间来存储无数的短信&#xff0c;但由于设备故障、意外删除或其他意外原因&#xff0c;您可能会丢失重要的对话。幸运的是&#xff0c;我们找到了 5 种有效的 Android SMS 备份解决方案&#xff0c;确保您的数字聊天和信息保持安全且可访问。…
阅读更多...
标题：2025海外短剧爆发年：APP+H5双端系统开发，解锁全球流量与变现新大陆

标题：2025海外短剧爆发年：APP+H5双端系统开发，解锁全球流量与变现新大陆

描述&#xff1a; 2025年出海新风口&#xff01;深度解析海外短剧系统开发核心&#xff08;APPH5双端&#xff09;&#xff0c;揭秘高效开发策略与商业化路径&#xff0c;助您抢占万亿美元市场&#xff01; 全球娱乐消费模式正在剧变。2025年&#xff0c;海外短剧市场已从蓝海…
阅读更多...
解决RAGFlow（v0.19.0）有部分PDF无法解析成功的问题。

解决RAGFlow（v0.19.0）有部分PDF无法解析成功的问题。

ragflow版本为&#xff1a;v0.19.0 1.解析的时候报错&#xff1a;Internal server error while chunking: Coordinate lower is less than upper。 看报错怀疑是分片的问题&#xff0c;于是把文档的切片方法中的“建议文本块大小”数值&#xff08;默认512&#xff09;调小&…
阅读更多...
c#基础08(数组)

c#基础08(数组)

文章目录 数组数组概念声明数组初始化数组赋值给数组访问数组元素 集合动态数组(ArrayList)使用foreach循环C#数组细节多维数组传递数组给函数参数数组 数组 数组概念 数组是一个存储相同类型元素的固定大小的顺序集合。数组是用来存储数据的集合&#xff0c;通常认为数组是一…
阅读更多...
嵌入式学习--江协stm32day3

嵌入式学习--江协stm32day3

这是我目前为止认为最重要的模块--TIM定时器&#xff0c;这里我们主要学习通用定时器 最小的计数计时单元为时基单元&#xff0c;包括PSC&#xff0c;ARR&#xff0c;CNT CK_PSC&#xff08;Prescaler&#xff0c;预分频器&#xff09;&#xff1a;作用是对输入时钟信号进行分…
阅读更多...
4.8.1 利用Spark SQL实现词频统计

4.8.1 利用Spark SQL实现词频统计

在利用Spark SQL实现词频统计的实战中&#xff0c;首先需要准备单词文件并上传至HDFS。接着&#xff0c;可以通过交互式方法或创建Spark项目来实现词频统计。交互式方法包括读取文本文件生成数据集&#xff0c;扁平化映射得到新数据集&#xff0c;然后将数据集转成数据帧&#…
阅读更多...
PyTorch中nn.Module详解

PyTorch中nn.Module详解

直接print(dir(nn.Module))&#xff0c;得到如下内容&#xff1a; 一、模型结构与参数 parameters() 用途&#xff1a;返回模块的所有可训练参数&#xff08;如权重、偏置&#xff09;。示例&#xff1a;for param in model.parameters():print(param.shape)named_parameters…
阅读更多...
动态表单开发避坑：改变input的值不会触发change事件即时修复策略-WdatePicker ——仙盟创梦IDE

动态表单开发避坑：改变input的值不会触发change事件即时修复策略-WdatePicker ——仙盟创梦IDE

原始传统模式 onchange <input onchange"未来之窗东方仙盟change(this)" oni > <script>function 未来之窗东方仙盟change(onj){console.log("未来之窗东方仙盟change",onj.value)} </script> 测试 原始传统模式 oninput <input …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023