图论part08

拓扑排序精讲

代码随想录讲解链接
题目链接

思路

• 在这个题目之中，个别文件的处理依赖于别的文件，因此，文件的处理顺序十分重要。
• 我们用图来表示文件的处理顺序，文件s指向文件t，则说明如果要正确的处理文件t，那么就必须先处理文件s。换句话说，文件t所对应的入度为1，当我们处理好文件s之后，文件t的入度就变成0，于是就可以处理文件t了。
• 同理，当我们将文件t处理之后，文件t指向的下一个文件x也就可以正常处理了（x入度为0），以此类推，最终根据结果集之中的文件个数可以正确的判断是否能够成功处理。

import java.util.*;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);

        int N = sc.nextInt();
        int M = sc.nextInt();
        // 构建图从而记录文件之间的依赖关系
        List<List<Integer>> umap = new ArrayList<>();
        // 记录每个文件的入度
        int[] inDegree = new int[N];

        
        for(int i = 0 ; i < N ; i++)
            umap.add(new ArrayList<>());

        // 填充边的关系
        for(int i = 0 ; i < M ; i++){
            int s = sc.nextInt();
            int t = sc.nextInt();
            umap.get(s).add(t); //表示s指向t
            inDegree[t] ++; //由于s指向t，所以t的入度加一
        }


        Queue<Integer> queue = new LinkedList<>();
        // 找出所有节点之中入度为0的节点
        for(int i = 0 ; i < N ; i++){
            if(inDegree[i] == 0){
                queue.add(i);
            }
        }
        List<Integer> result = new ArrayList<>();

        // 拓扑排序流程
        while(!queue.isEmpty()){
            int cur = queue.poll();
            result.add(cur);
            // 上面将节点cur加入到结果集之后，cur指向的所有节点的入度都应该减1
            for(int nextNode : umap.get(cur)){
                inDegree[nextNode] --;
                // 当某个节点的入度为0的时候，将其添加到队列之中
                if(inDegree[nextNode] == 0){
                    queue.add(nextNode);
                }
            }
        }
        // 在这里如果结果集之中的记录个数等于文件个数，则证明这些文件可以正常处理。
        // 若果结果集之中的记录个数小于文件个数，这证明这些文件的依赖一定存在环。
        if(result.size() == N){
            for(int i = 0 ; i < N - 1 ; i++){
                System.out.print(result.get(i)+" ");
            }
                System.out.print(result.get(N - 1 ));
        }else{
            System.out.println(-1);
        }
    }
}

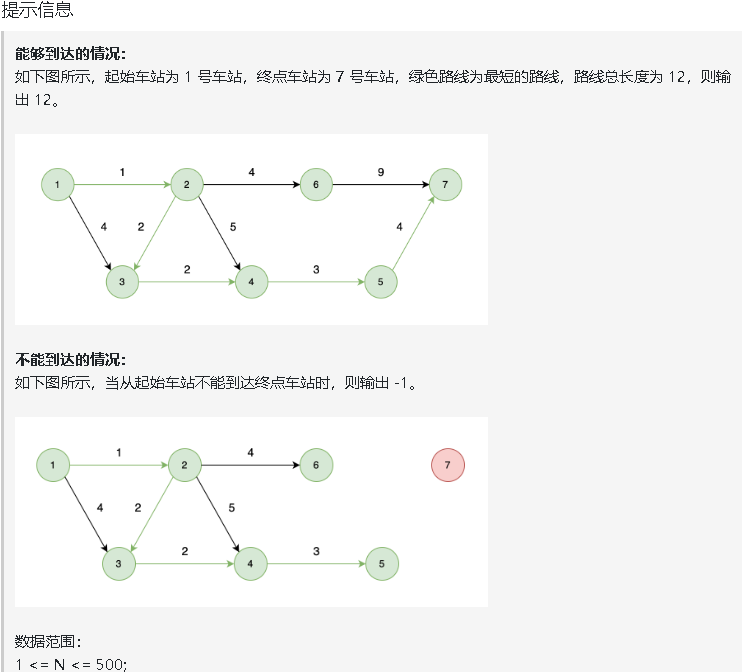
dijkstra（朴素版）精讲

代码随想录链接
题目链接

import java.util.*;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();

        int[][] graph = new int[n+1][n+1];

        for(int i = 0 ; i <= n ; i++)
            Arrays.fill(graph[i],Integer.MAX_VALUE);

        for(int i = 0 ; i < m ; i++){
            int s = sc.nextInt();
            int t = sc.nextInt();
            int val = sc.nextInt();
            graph[s][t] = val;
        }
        int start = 1;
        int end = n;

        // 存储原点到每个节点的最短距离
        int[] minDis = new int[n + 1];
        Arrays.fill(minDis,Integer.MAX_VALUE);


        // 判断当前的节点是否已经被访问过

        boolean[] visted = new boolean[n+1];

        // 原点到自身的距离为0
        minDis[start] = 0;

        for(int i = 1 ; i <= n ; i++){
            // 初始化用于记录的最小值和当前节点

            int minVal = Integer.MAX_VALUE;
            int cur = 1;


            // 寻找val最小的边
            for(int v = 1 ; v <= n ; v++){
                if(!visted[v] && minDis[v] < minVal){
                    cur = v;
                    minVal = minDis[v];
                }
            }

            visted[cur] = true;

            // 更新minDis数组

            for(int v = 1 ; v <= n ; v++ ){
                if(!visted[v] && graph[cur][v] != Integer.MAX_VALUE && minDis[cur] + graph[cur][v] < minDis[v] ){
                    minDis[v] = minDis[cur] + graph[cur][v];
                }
            }
        }

        if (minDis[end] == Integer.MAX_VALUE) {
            System.out.println(-1); // 不能到达终点
        } else {
            System.out.println(minDis[end]); // 到达终点最短路径
        }
    }
}