一、一元函数:
在实际应用中,经常需要近似计算函数y=f(x)的增量Δy=f(x)-f(x0)=f(x0+Δx)-f(x0),其中一种近似称为函数的微分。
定义:若函数y=f(x)在点x0处的增量Δy可表达为自变量增量Δx的线性函数AΔx和Δx的高阶无穷小量之和,即Δy=f(x0+Δx)-f(x0)=AΔx+o(Δx),(Δx->0)
其中,A是不依赖于Δx的某一常数,则称函数y=f(x)在点x0处可微,并记函数y=f(x)在点x0处的微分为dy|x=x0=df|x=x0=AΔx=Adx
定理:函数y=f(x)在点x0处可微的充要条件为函数y=f(x)在点x0处可导,且dy|x=xo=f'(x0)dx
函数可微性的几何意义:函数在某点附近可用其切线近似表示(不是等于,极限也不相等)(当Δx->0,(Δy-dy)/Δx->0)
函数的导数y'=dy/dx可用函数微分dy和自变量微分dx之比表示
(1)为什么可微一定可导?
对于一元函数f(x),若在x=a处可微,表函数在该点有一个局部线性化的形式,存在一个常数f'(a),使得在a点附近,函数值的变化可以通过下式近似:f(a+h)~~f(a)+f'(a)h(当h->0时),也就是说,函数的增量可以通过线性项f'(a)h来近似。f'(a)即是f(x)在x=a处的导数。
(2)为什么可导一定可微?
可微:函数f(x)在某点x=a处可微,意味着函数在该点具有一个明确的局部线性逼近,存在切线。即,函数可以写成:f(a+h)≈f(a)+f′(a)h
更严格地说,如果函数可微,那么存在常数f'(a),使得:
f(a+h)-f(a)-f'(a)h
lim ________________=0
h->0 h
推导过程:
1、根据导数定义,函数在点x=a处可导,意味着:
f(a+h)-f(a)
f'(a)=lim_______________
h->0 h
现在要证明函数在点a处是可微,即证明:
f(a+h)-f(a)-f'(a)h
lim ________________=0
h->0 h
这意味着函数在a点处的增量可以被线性化,剩下的误差项趋于 0。
2、先将增量f(a+h)-f(a)分解成两部分:
f(a+h)-f(a)=f'(a)h+o(h)
其中,o(h)表示高阶无穷小,意味着o(h)相对于h增长得更慢(即o(h)/h→0当h→0时)。【为什么可以这样分?】(资料上说:导数的定义和极限的性质)
3、代入:
f(a+h)-f(a)-f'(a)h o(h)
________________ = ________
h h
4、由于o(h)是高阶无穷小,满足o(h)/h->0当h->0时,因此:
o(h)
lim ___ =0
h->0 h
这就证明了:
f(a+h)-f(a)-f'(a)h
lim ________________ =0
h->0 h
从而证明了函数在点a处是可微的。
(3)可导一定连续。连续不一定可导(y=|x|在x=0处不可导)。
证明:由于,f'(x0)存在,所以
f'(x0)=lim*{x->x0} [f(x)-f(x0)]/(x-x0)存在,从而
lim*{x->x0} [f(x)-f(x0)]=lim*{x->x0} [f(x)-f(x0)]/(x-x0) • (x-x0)=0
即 lim*{x->x0} f(x)=f(x0)
所以,f(x)在点x0处连续
二、二元函数
(1)可微必连续(连续必可微??)
多元函数连续性定义:
设函数f(x,y)在点p。(x。,y。)的某个邻域内有定义,如果limf(x,y)=f(x。,y。),则称函数f(x,y)在点p。处连续。 x->x。
y->y。
证明:
根据可微性的定义:
f(a+Δx,b+Δy)−f(a,b)=fx(a,b)Δx+fy(a,b)Δy+o(ρ)
其中 o(ρ) 是比ρ更小 的高阶无穷小。
两边取极限:
Δx,Δy→0lim[f(a+Δx,b+Δy)−f(a,b)]=Δx,Δy→0lim[fx(a,b)Δx+fy(a,b)Δy+o(ρ)]
由于Δx,Δy→0时fx(a,b)Δx和 fy(a,b)Δy也趋于 0,而 o(ρ) 是高阶无穷小,也趋于 0,因此右边极限为 0。
所以我们得到:limΔx,Δy→0[f(a+Δx,b+Δy)−f(a,b)]=0
这正是函数f(x,y)在(a, b)处连续性的定义:(x,y)->(a,b)limf(x,y)=f(a,b)
(2)可微必可导


(3)可导不一定可微,可导不一定连续(连续必可导??)
xy
_______
x^2+y^2 ,x^2+y^2<>0
例如f(x,y)={
0, x^2+y^2=0
f(x,y)在原点(0,0)处的两个导数:fx(0,0)=Δx->0lim[f(0+Δx,0)-f(0,0)]/Δx=0同理fy(0,0)=0
都存在,但在原点(0,0)处不连续,从而在原点(0,0)处不可微。这是因为:假如函数f(x,y)在原点(0,0)处可微,则它必连续,从而矛盾。
三、偏导数
(1)偏导数的几何意义
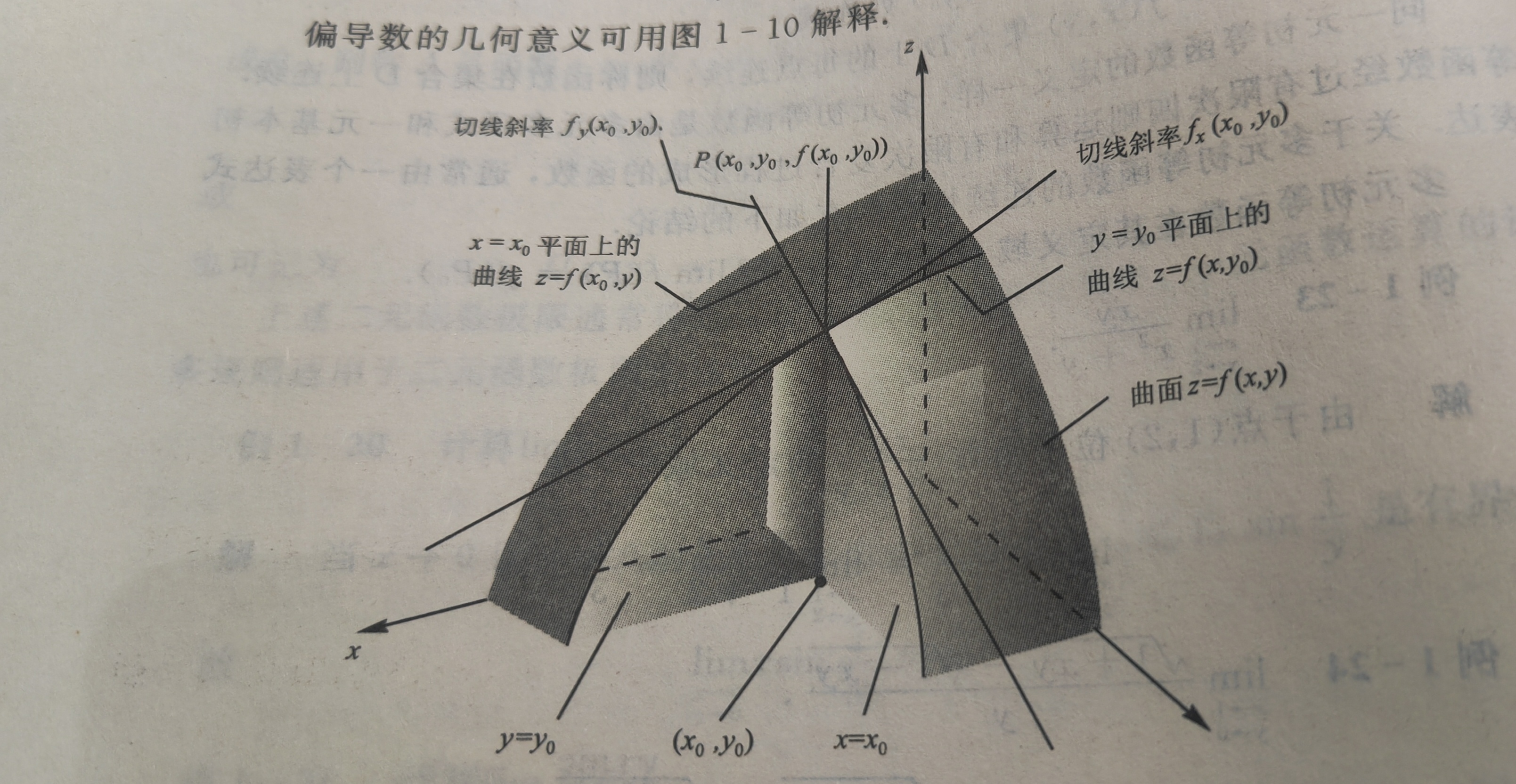
(2)证明:函数z=√(x^2+y^2)在(0,0)处连续,但两个偏导数都不存在。
1)原函数的图像是一个以原点(0,0,0)为顶点的圆锥面。无论从任何方向接近顶点,高度z都会逐渐降低到0,没有跳跃或空洞。这种几何形状表明,函数在原点处是平滑连接的因此连续
2)
(1)当点(x,y)接近于0时,距离公式的值趋近于0。
(2)计算极限值:
lim*(x,y)->(0,0)√(x^2+y^2)=√(0^2+0^2)=0
(3)比较极限值与函数值:
f(0,0)=0
结论:极限值等于函数值,因此函数在(0,0)处连续
3)
(a)对x的偏导数:
fx(0,0)=lim*h->0(f(h,0)-f(0,0))/h=lim*h->0(
√h^2-0)/h=lim*h->0(|h|/h)
当 h -> 0^+ 时,|h|/h = 1 ;
当 h ->0^- 时,|h|/h} = -1 。
由于左右极限不相等,极限不存在,故fx在(0,0)处极限不存在。
(b)
同理:对y的偏导数fy在(0,0)处也不存在。
(3)复合函数和隐函数的偏导数
(1)F(x)=0对定义域的所有x恒成立,则F'(x)=0(理解:导数是函数值随x的变化率)
(2)应用:单位圆方程x^2+y^2=1确定了一个y(x)的隐函数。
F(x,y)=x^2+y^2-1
dF[x,y(x)]/dx=0 理解:此时看作对x求导,y看作关于x的中间变量
2x+2y*(dy/dx)=0 理解:隐函数求导结果包含y,不用化简
结论1:
隐函数是一元函数
dy/dx=-Fx/Fy
Fx是二元函数对x的偏导,Fy是二元函数对xpy的偏导
结论2:
隐函数是二元函数
∂z/∂x=-Fx/Fz
∂z/∂y=-Fy/Fz
四、偏导数的应用-极值与最值
a.一元函数:
极值含义:1)
函数y=f(x)在点x0的某邻域(x0-Δx,x0+Δx)中有定义,x0是函数在(x0-Δx,x0+Δx)内的最值点
最值:连续函数y=f(x)在区间[a,b]上的最大值(最小值类似)问题时,最大值只能是函数的驻点,不可导点或区间的端点
设函数f(x)在点x0处取到极值,且y=f(x)在点x0处可导,则必有f'(x0)=0
若x0是极值点,则要么f'(x0)=0,要么函数y=f(x)在x0处不可微,驻点不一定是极值点(y=x^3,x=0)
函数的极值点通常出现在驻点或不可导点(??)
设函数y=f(x)在点xo的某邻域(x0-Δx,x0+Δx)上有定义,且x0是y=f(x)的驻点或 y=f(x)在点x0处不可导,则:
如果f'(x0)=0,且f''(x0)<0,则x=x0为函数y=f(x)的极大值点(极小值点类似)??
b.二元函数的极值与最值:
设f(x0,y0)是函数z=f(x,y)的极值点,且函数z=f(x,y)在点(x0,y0)处偏导数存在,则fx(x0,y0)=0,fy(x0,y0)=0;
类似于一元函数的讨论,同时使得fx(x,y)=0,fy(x,y)=0的点(x0,y0)称为函数z=f(x,y)的驻点(在函数可导的条件下,极值点必为驻点);
在极值点处函数的所有偏导数必定为0或至少一个偏导数不存在(z=✔️(x^2+y^2))。但驻点却不一定是极值点(z=y^2-x^2)。
五、偏导数的应用—梯度
设z=f(x,y)在平面区域D上有定义,点(x,y)属于D,l是一个向量,记l的方向余弦为(cosa,sina),即(cosa,sina)=l,其中a为从x轴正向到向量l的转角。

 例1:
例1:

 例2:
例2:

 六、偏导数的应用—切平面和法平面
六、偏导数的应用—切平面和法平面
1)法平面


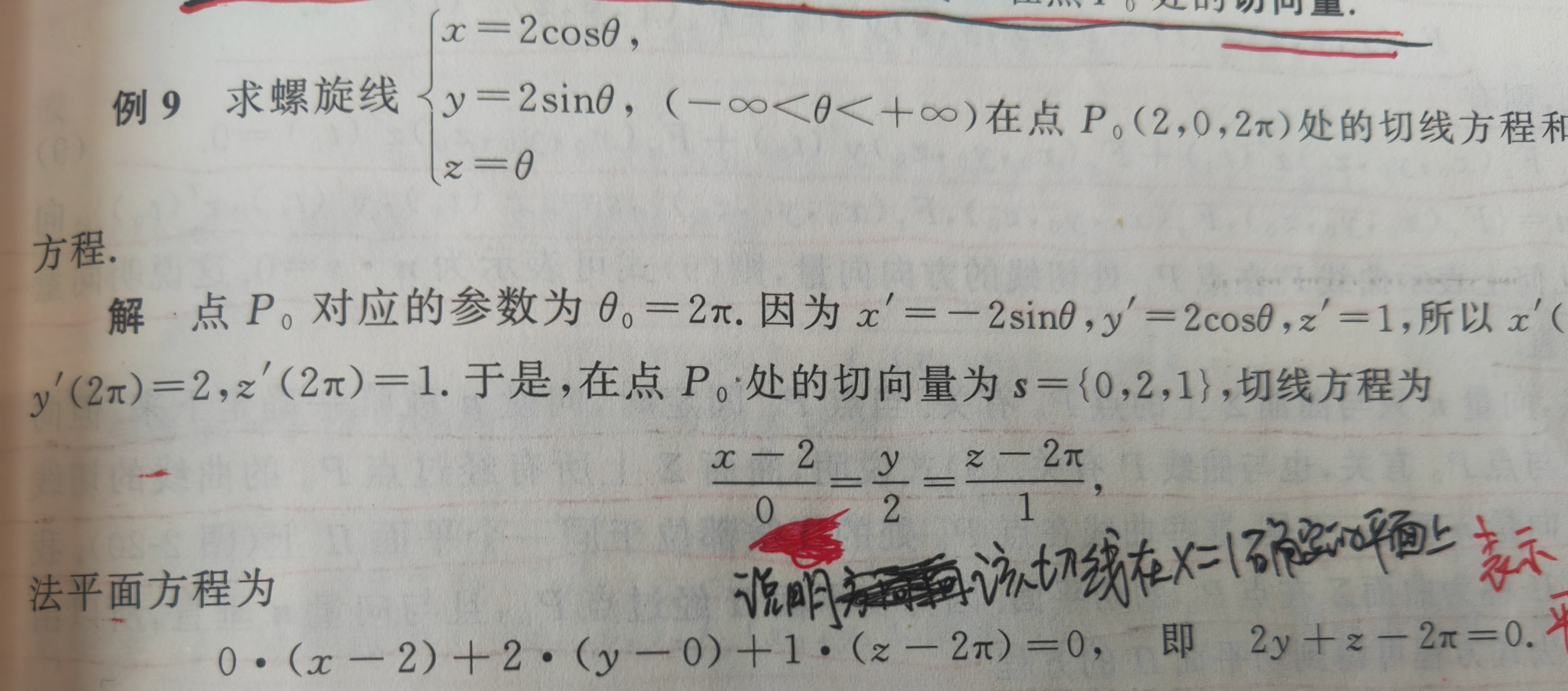
2)切平面
设曲面Σ的一般方程为F(x,y,z)=0,其中F(x,y,z)具有连续的偏导数。设曲面上过点P0(x0,y0,z0)的曲线
x=x(t)
{ y=y(t) 满足x(t0)=x0,y(t0)=y0,z(t0)=z0。由于曲线在曲面Σ上,则F(x(t),y(t),z(t))=0,对t求导得:
z=z(t)
Fxx'(t)+Fyy'(t)+Fzz'(t)=0
令t=t0得
Fx(P0)x'(t0)+Fy(P0)y'(t0)+Fz(P0)z'(t0)=0
上式表明向量(Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0))垂直于曲面上任意过点P0(x0,y0,z0)处的曲线的切向量,因此(Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0))就是曲面在点P0(x0,y0,z0)处的切平面π的法向量,即曲面上点P0(x0,y0,z0)处的法向量n
由此得到曲面上的点P0(x0,y0,z0)处的切平面π方程为Fx(P0)(x-x0)+Fy(P0)(y-y0)+Fx(P0)(z-z0)=0
法线方程:(x-x0)/Fx(P0)=(y-y0)/Fy(P0)=(z-z0)/Fz(P0)
若曲面方程为一般方程:f(x,y)-z=0 法向量为n=(fx(x0,y0),fy(x0,y0),-1),切平面方程为fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0)-(z-f(x0,y0))=0
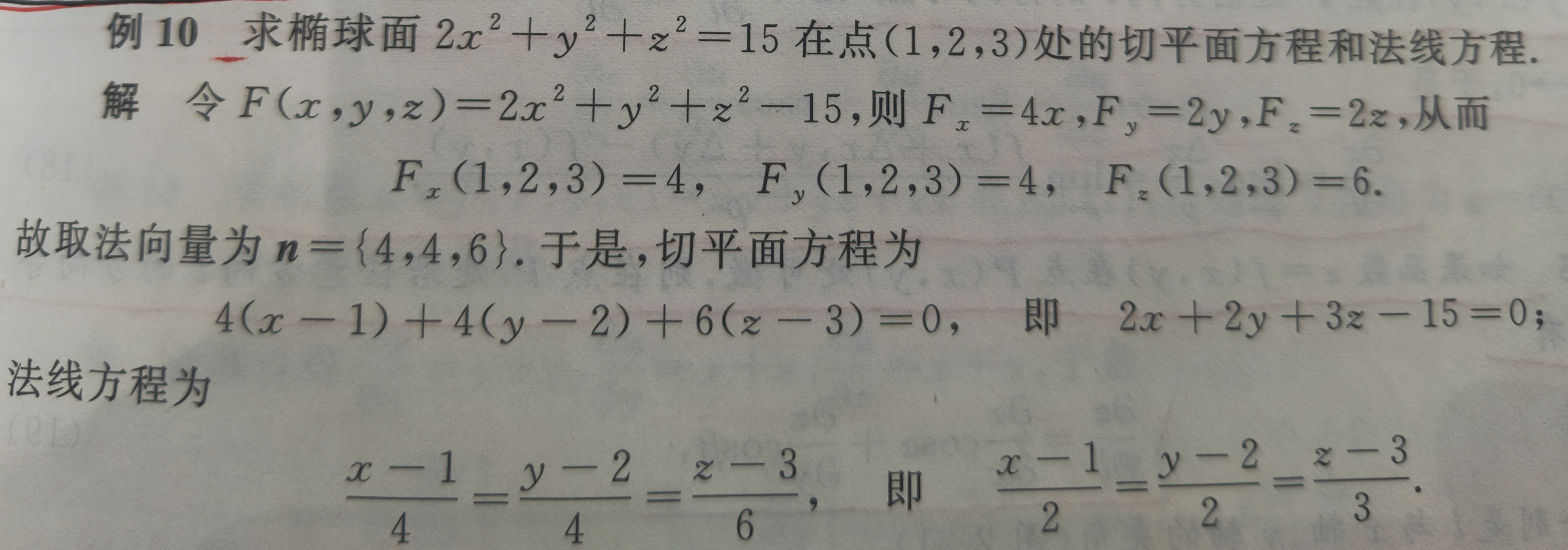



注:(1)曲面上一点的法向量(根据曲面函数的偏导函数计算)只与点的坐标有关,只要点的坐标确定,该法向量就确定,法向量的方向余弦同样只与点的坐标有关,所以曲面上点的法向量的方向余弦是关于x,y(针对曲面由方程z=f(x,y)给出)的二元函数。