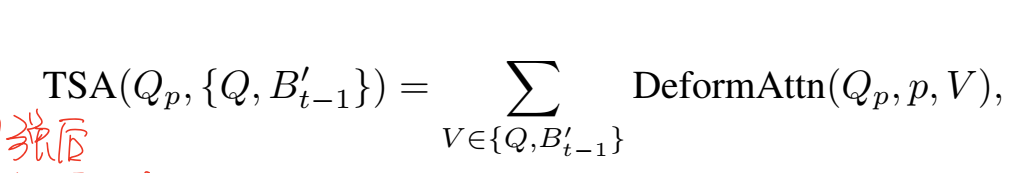题目列表
3541. 找到频率最高的元音和辅音
3542. 将所有元素变为 0 的最少操作次数
3543. K 条边路径的最大边权和
3544. 子树反转和
一、找到频率最高的元音和辅音

分别统计元音和辅音的出现次数最大值,然后相加即可,代码如下
// C++
class Solution {
const string str = "aeiou";
public:
int maxFreqSum(string s) {
int cnt[26]{};
int mx1 = 0, mx2 = 0;
for(auto & e : s){
cnt[e - 'a']++;
if(str.find(e) == string::npos){
mx1 = max(mx1, cnt[e - 'a']); // 更新辅音
}else{
mx2 = max(mx2, cnt[e - 'a']); // 更新辅音
}
}
return mx1 + mx2;
}
};
# Python
class Solution:
def maxFreqSum(self, s: str) -> int:
cnt = [0] * 26
mx1 = 0
mx2 = 0
for e in s:
x = ord(e) - ord('a')
cnt[x] += 1
if e in "aeiou":
mx1 = max(mx1, cnt[x])
else:
mx2 = max(mx2, cnt[x])
return mx1 + mx2
二、将所有元素变为 0 的最少操作次数

本题的难点在于一旦我们将区间内的最小值变为 0,那么剩余的不为 0 的数字就会被分成一段一段的区间,此时,我们需要在这些区间内再去进行操作,而这需要我们维护区间内的最小值,显然很困难,那有没有什么其他的思路?
-
思路
对于一个数字x来说,只有当它是区间内的最小值时,才可以通过操作被置为0,而从贪心的角度来说,这个区间越大,则置为0的数越多,所进行的操作就会越少。所以我们只要计算对于同一个数字x,它需要被分为多少个区间,才能让所有的x全部变为0,而它分出的区间数就是它需要进行的最少操作次数。统计所有的数字对于答案的贡献即可- 这里暗含一个贪心的策略,优先将小的数字置为
0会更优,因为小的数字置为0,它依旧是小的数字,不会影响大的数字的分区个数,但是反过来,大的数字置为0,就有可能将小的数字分成更多的区间,导致操作次数变多 - 故这里我们计算出每个数字区间个数后直接相加,看似不论顺序,实质是从小的数字开始进行操作
- 求解
x为最小数字的区间,本质是求距离x最近的比它小的数字下标,可以用单调栈来求解
- 这里暗含一个贪心的策略,优先将小的数字置为
// C++
class Solution {
public:
int minOperations(vector<int>& nums) {
int n = nums.size();
stack<int> st;
vector<int> left(n, -1), right(n, n);
// 计算区间
for(int i = 0; i < n; i++){
while(st.size() && nums[st.top()] > nums[i]){
right[st.top()] = i;
st.pop();
}
st.push(i);
}
st = stack<int>();
for(int i = n - 1; i >= 0; i--){
while(st.size() && nums[st.top()] > nums[i]){
left[st.top()] = i;
st.pop();
}
st.push(i);
}
unordered_map<int,set<pair<int,int>>> mp;
for(int i = 0; i < n; i++){
mp[nums[i]].emplace(left[i], right[i]);
}
int ans = 0;
for(auto& [x, st] : mp){
if(x){ // x = 0 不需要进行操作
ans += st.size();
}
}
return ans;
}
};
-
优化
- 对于求区间个数的操作,我们可以在一次循环中得到,具体如下
// C++
class Solution {
public:
int minOperations(vector<int>& nums) {
int n = nums.size(), ans = 0;
stack<int> st; // 单调递增 & 栈中无重复数字 & 不包含 0
for(int i = 0; i < n; i++){
while(st.size() && nums[st.top()] >= nums[i]){
// 这里只统计一定需要进行一次操作的数字个数,即左右边界已经明确的数字
// 和 nums[i] 相同的数字,由于右边界还不确定,此处不统计,等区间明确后在统计
if(nums[st.top()] != nums[i]){
ans++;
}
st.pop();
}
if(nums[i]) // 0 不需要入栈
st.push(i);
}
// 栈中剩余的数字,此时右边界已经确定,也需要进行一次操作才能被置为 0
return ans + st.size();
}
};
#Python
class Solution:
def minOperations(self, nums: List[int]) -> int:
ans = 0
bottom, top = 0, 0 # 可以直接将 nums 当作栈进行使用,空间复杂度为 O(1)
for i in range(len(nums)):
while bottom != top and nums[top-1] >= nums[i]:
if nums[top-1] != nums[i]:
ans += 1
top -= 1
if nums[i] > 0:
nums[top] = nums[i]
top += 1
return ans + top - bottom
三、K 条边路径的最大边权和

本题先建图,然后直接用 dfs 进行遍历即可,注意,为了防止重复遍历某个状态,需要记忆化已经遍历过的状态,代码如下
// C++
class Solution {
public:
int maxWeight(int n, vector<vector<int>>& edges, int k, int t) {
vector<vector<pair<int,int>>> g(n);
for(auto& e : edges){
g[e[0]].emplace_back(e[1], e[2]);
}
int ans = -1;
set<tuple<int,int,int>> st; // 记忆化遍历过的状态
auto dfs = [&](this auto&& dfs, int x, int d, int s)->void{
if(d == k){
ans = max(ans, s);
return;
}
if(st.count({x, d, s}))
return;
st.emplace(x, d, s);
for(auto& [y, w] : g[x]){
if(s + w < t){
dfs(y, d + 1, w + s);
}
}
};
for(int i = 0; i < n; i++){
dfs(i, 0, 0);
}
return ans;
}
};
# Python
class Solution:
def maxWeight(self, n: int, edges: List[List[int]], k: int, t: int) -> int:
g = [[] for _ in range(n)]
for x, y, w in edges:
g[x].append((y, w))
ans = -1
@cache
def dfs(x:int, d:int, s:int):
if d == k:
nonlocal ans
ans = max(ans, s)
return
for y, w in g[x]:
if w + s < t:
dfs(y, d + 1, w + s)
for i in range(n):
dfs(i, 0, 0)
return ans
四、子树反转和

本题的反转操作有距离限制,也就是说对当前结点进行反转操作之后,与它距离小于 k 的结点就不能进行反转操作了,所以我们在 dfs 遍结点的时候,需要增加两个参数 mul : 表示当前的结点取正还是取负,cd : 多少距离后,就能再次进行反转操作,故我们有 dfs(x,fa,mul,cd)
- 当
x结点不反转时, d f s ( x , f a , m u l , c d ) = s u m ( d f s ( y , x , m u l , ( c d ? c d − 1 , 0 ) ) ) + ( m u l ? n u m s [ x ] : − n u m s [ x ] ) dfs(x,fa,mul,cd)=sum(dfs(y,x,mul,(cd\ ?\ cd-1,0)))+(mul\ ?\ nums[x]\ : \ -nums[x]) dfs(x,fa,mul,cd)=sum(dfs(y,x,mul,(cd ? cd−1,0)))+(mul ? nums[x] : −nums[x]),其中y是结点x的所有子节点 - 当
x结点反转且cd == 0时, d f s ( x , f a , m u l , c d ) = s u m ( d f s ( y , x , ! m u l , k − 1 ) ) + ( m u l ? − n u m s [ x ] : n u m s [ x ] ) dfs(x,fa,mul,cd)=sum(dfs(y,x,!mul,k-1))+(mul\ ?\ -nums[x]\ : \ nums[x]) dfs(x,fa,mul,cd)=sum(dfs(y,x,!mul,k−1))+(mul ? −nums[x] : nums[x]),其中y是结点x的所有子节点
代码如下
// C++
class Solution {
public:
long long subtreeInversionSum(vector<vector<int>>& edges, vector<int>& nums, int k) {
int n = nums.size();
vector<vector<int>> g(n);
for(auto & e : edges){
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
vector memo(n, vector(2, vector<long long>(k, -1)));
auto dfs = [&](this auto&& dfs, int x, int fa, bool mul, int cd)->long long{ // f0, cd0, f1
if(memo[x][mul][cd] != -1) return memo[x][mul][cd];
long long res = mul ? nums[x] : -nums[x];
for(int y : g[x]){
if(y != fa){
res += dfs(y, x, mul, (cd ? cd - 1 : 0));
}
}
if(cd == 0){
long long res2 = mul ? -nums[x] : nums[x];
for(int y : g[x]){
if(y != fa){
res2 += dfs(y, x, !mul, k - 1);
}
}
res = max(res, res2);
}
return memo[x][mul][cd] = res;
};
return dfs(0, -1, true, 0);
}
};
# Python
class Solution:
def subtreeInversionSum(self, edges: List[List[int]], nums: List[int], k: int) -> int:
n = len(nums)
g = [[] for _ in range(n)]
for x,y in edges:
g[x].append(y)
g[y].append(x)
memo = {}
def dfs(x:int, fa:int, mul:bool, cd:int)->int:
t = (x, mul, cd)
if t in memo:
return memo[t]
res = nums[x] if mul else -nums[x]
for y in g[x]:
if y != fa:
res += dfs(y, x, mul, cd - 1 if cd > 0 else 0)
if cd == 0:
res2 = -nums[x] if mul else nums[x]
for y in g[x]:
if y != fa:
res2 += dfs(y, x, not mul, k - 1)
res = max(res, res2)
memo[t] = res
return res
return dfs(0, -1, True, 0)





![【离散化 线段树】P3740 [HAOI2014] 贴海报|普及+](https://i-blog.csdnimg.cn/img_convert/6d5e5f1ce0c750699da2fc655a991b4c.png)