参考程序：

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <string>
#include <map>
#include <iostream>
#include <cmath>
#include <vector>
#include <queue>
using namespace std;
const int N = 100005;
int fa[N], sz[N], dep[N], son[N], tp[N], mxId[N];
// fa[i]：i的父节点编号（管理者）
// sz[i]：以i为根的子树大小
// dep[i]：i节点的深度
// son[i]：i的重儿子（子树最大的儿子）
// tp[i]：i所在重链的顶端节点
// mxId[i]：从根走到i路径上的最大编号员工

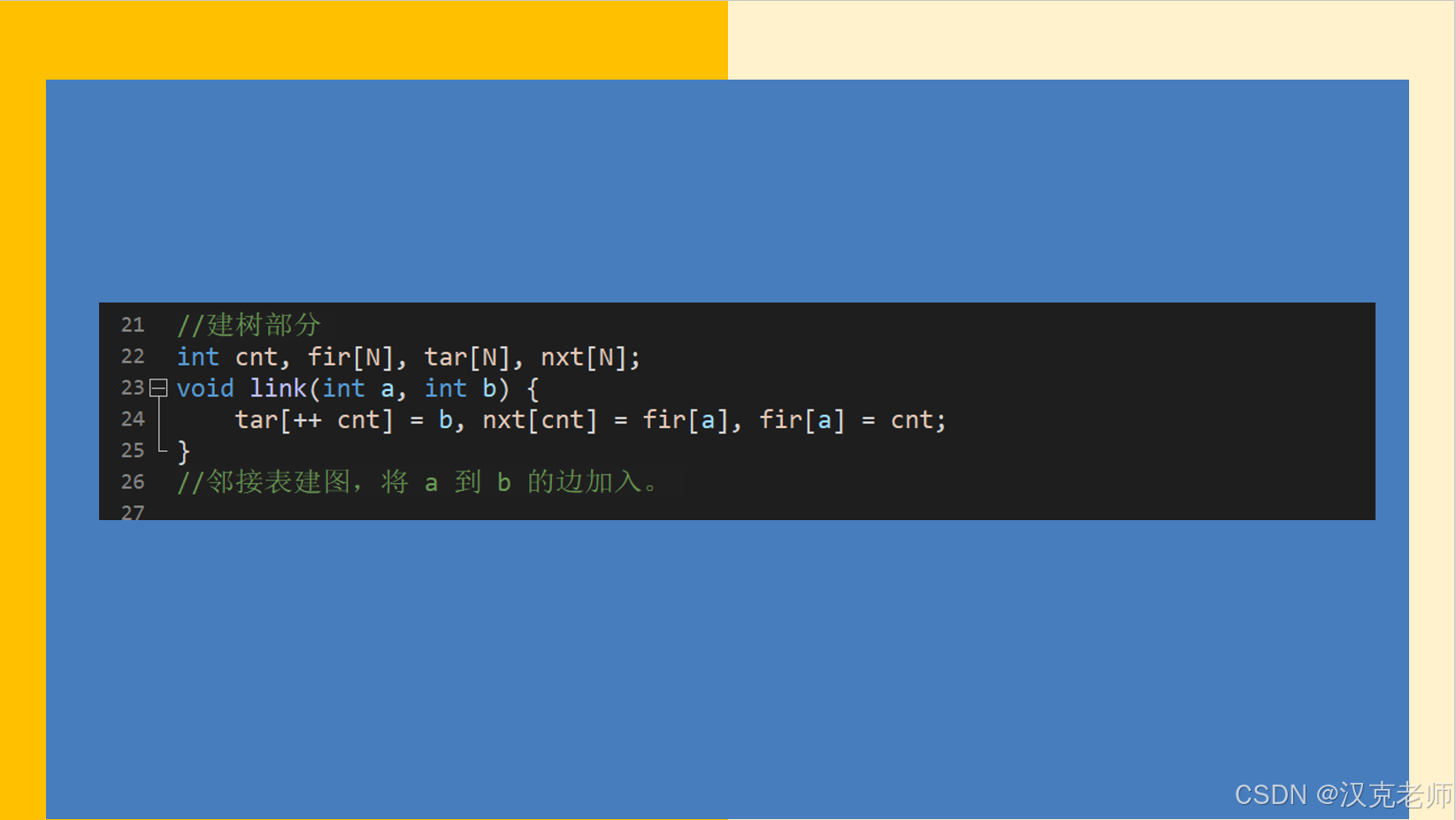
//建树部分 
int cnt, fir[N], tar[N], nxt[N];
void link(int a, int b) {
	tar[++ cnt] = b, nxt[cnt] = fir[a], fir[a] = cnt;
}  
//邻接表建图，将 a 到 b 的边加入。 

//树形DP初始化 + 最大编号路径记录
void dfs(int x, int mxid) {
    int Mx = 0;                          // 用来记录最大的子树大小
    sz[x] = 1;                           // 初始化 x 的子树大小为 1（自己本身）
    mxId[x] = max(x, mxid);             // 更新从根到 x 路径上的最大编号

    for (int i = fir[x]; i; i = nxt[i]) {
        dep[tar[i]] = dep[x] + 1;        // 设置子节点的深度
        dfs(tar[i], mxId[x]);            // 递归子节点，传入当前路径的最大编号
        sz[x] += sz[tar[i]];             // 回溯后更新当前节点的子树大小
        if (Mx < sz[tar[i]])
            Mx = sz[son[x] = tar[i]];    // 找到最大的子树，作为重儿子
    }
}

//DFS 过程中完成：
//子树大小 sz[x] 计算；
//深度 dep[x] 记录；
//重儿子 son[x] 查找；
//从根到当前节点路径上的最大编号员工 mxId[x] 记录。

//重链剖分中的 top 结点标记
void gettp(int x) {
    tp[x] = x;
    if (son[fa[x]] == x)
        tp[x] = tp[fa[x]];  // 若是重儿子，则继承父亲的链头
    for (int i = fir[x]; i; i = nxt[i])
        gettp(tar[i]);
}

//用于 LCA 快速跳链优化。

//最近公共祖先（LCA）
int lca(int x,int y){
    while (tp[x] != tp[y])  // 不在同一条链
        dep[tp[x]] > dep[tp[y]] ? x = fa[tp[x]] : y = fa[tp[y]];
    return dep[x] < dep[y] ? x : y;
}
//利用重链剖分实现 LCA 查询。
//时间复杂度为 O(logN)。


int main() {
    int n;
    scanf("%d", &n);
    for(int i = 2; i <= n; i ++)
        scanf("%d", &fa[i]), link(++ fa[i], i);  // 注意索引偏移：fa[i] + 1（因为原始编号0开始）

    dfs(1, 1), gettp(1);

    int q;
    scanf("%d", &q);
    while(q --) {
        int m, x, y;
        scanf("%d%d", &m, &x), x ++;  // 统一编号 +1
        for(int i = 2; i <= m; i ++) {
            scanf("%d", &y);
            x = lca(x, ++ y);  // 所有员工的公共祖先
        }
        cout << mxId[x] - 1 << endl;  // 注意编号减回去
    }
    return 0;
}