数据结构-非线性结构-二叉树

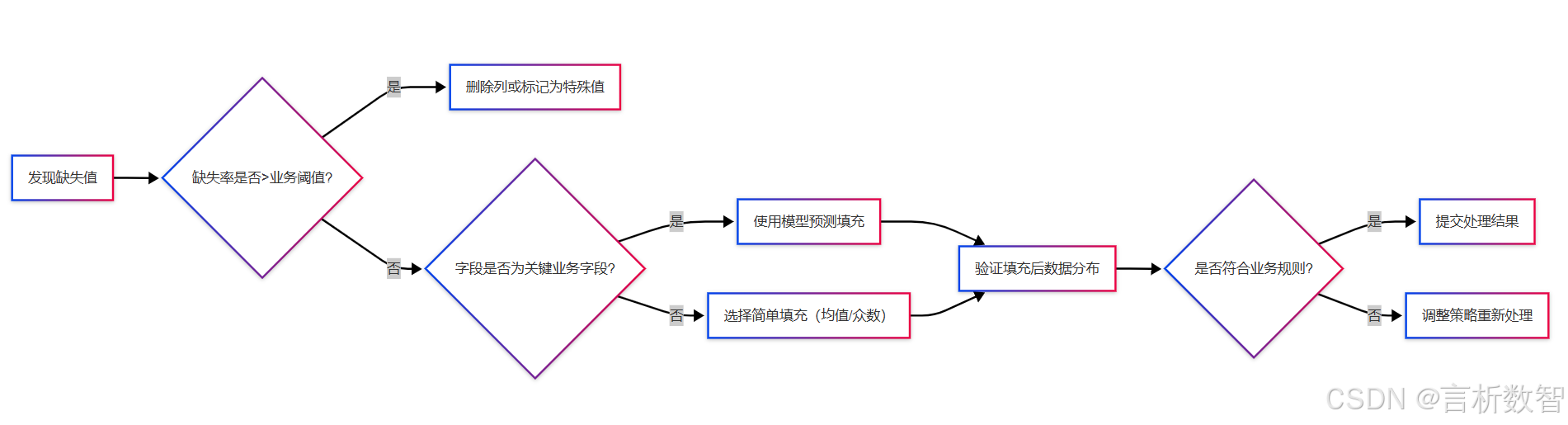
概述

/**

* 术语

* 根节点（root node）：位于二叉树顶层的节点，没有父节点。

* 叶节点（leaf node）：没有子节点的节点，其两个指针均指向 None 。

* 边（edge）：连接两个节点的线段，即节点引用（指针）。

* 节点所在的层（level）：从顶至底递增，根节点所在层为 1 。

* 节点的度（degree）：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。

* 二叉树的高度（height）：从根节点到最远叶节点所经过的边的数量。

* 节点的深度（depth）：从根节点到该节点所经过的边的数量。

* 节点的高度（height）：从距离该节点最远的叶节点到该节点所经过的边的数量。

*/

/**

* 二叉树遍历：【前序、中序、后序】->【递归遍历实现、非递归遍历实现（栈实现）】、层次遍历（队列实现）

* 二叉查找树：具有性质如下的二叉树：对于任一结点，如果它包含的数据元素为data，

* 那么它的左子树（如果非空）只包含小于data的元素，并且它的右子树（如果非空）只包含大于或等于data的元素。

* 中序遍历二叉查找树将会得到从小到大排列的结点序列。

* 二叉线索树：通过利用原本指向空子节点（即 NULL 指针）的空间来指向前驱或后继节点，从而在遍历时不需要使用额外的栈或递归。

* 这种结构特别适用于那些需要频繁遍历而修改较少的应用场景。

* 平衡二叉树：AVL树、红黑树

* 关键特性：左右子树高度差的绝对值不超过1

* 完全二叉树：主要用于实现堆（最大堆、最小堆）、哈夫曼编码

* 关键特性：按层次填充，每一层（除了最后一层）都完全填满，最后一层从左到右依次填充，没有间断

* 满二叉树：一种特殊的二叉树，每一层的节点都完全填满的二叉树

*/

/**

* 递归遍历

* 前序遍历：访问顺序为“根-左-右”。即先访问根节点，然后依次递归遍历左子树和右子树。

* 中序遍历：访问顺序为“左-根-右”。即先递归遍历左子树，然后访问根节点，最后递归遍历右子树。

* 后序遍历：访问顺序为“左-右-根”。即先递归遍历左子树，然后递归遍历右子树，最后访问根节点。

*/

/**

* 红黑树

* 红黑树的一些基本特性和规则：

* 每个节点要么是红色，要么是黑色。

* 根节点是黑色。

* 所有叶子节点（NIL节点，通常不显示在图中）都是黑色的。

* 如果一个节点是红色，则它的两个子节点都是黑色（即不能有两个连续的红色节点）。

* 从任一节点到其每个叶子的所有路径都包含相同数量的黑色节点。

*/

// 难点：遍历、旋转、删除

common.h

#pragma once

#define TRUE 1
#define FALSE 0

// 定义节点数据类型
#define DATA_TYPE int

二叉树插入、删除、递归遍历

BinaryTree.h

#pragma once

#include "common.h"

typedef struct Node
{
    DATA_TYPE data;
    struct Node *left;
    struct Node *right;
} Node;

// 创建一个树结点
static Node *newBinaryTreeNode(DATA_TYPE data)
{
    Node *node = malloc(sizeof(Node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 旋转节点使二叉树平衡
Node *rotate(Node *node);

// 向二叉树插入数据 平衡化重构
Node *insertNode(Node *T, DATA_TYPE data); // 递归

void insertNode_root(DATA_TYPE data); // 插入、从root开始
void insertData(DATA_TYPE data);           // 迭代 不会选择平衡化

// 返回二叉树结点数
int size();

// 节点高度
int height(Node *T);

// 前序、中序、后序遍历
void preOrder(Node *T);
void inOrder(Node *T);
void postOrder(Node *T);
// 逆中序打印二叉树
void printTree(Node *T, int level);

// 判断二叉树是否平衡
int is_balanced(Node *T);

// 查找数据是否在二叉树中
int search_val(DATA_TYPE val);

// 二叉树的root结点
Node *getRoot();

// 删除节点
Node *delete_data(DATA_TYPE val);

// 清空二叉树
void clear();

void test_binary_tree();

BinaryTree.c

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#include "BinaryTree.h"

#define MAX_LINE 1024 // 定义二叉树每行包含节点的最大个数 2的指数

static Node *root = NULL;
static int node_size = 0;

/*********************二叉树平衡化*********************/
// 获取平衡因子
static int balanceFactor(Node *node)
{
    if (node == NULL)
    {
        return 0;
    }
    return height(node->left) - height(node->right);
}

static Node *leftRotate(Node *node)
{
    Node *right = node->right;
    node->right = right->left;
    right->left = node;
    return right;
}

static Node *rightRotate(Node *node)
{
    Node *left = node->left;
    node->left = left->right;
    left->right = node;
    return left;
}

// 旋转节点使二叉树平衡
Node *rotate(Node *node)
{
    int bf = balanceFactor(node);
    if (bf > 1) // 左子树
    {
        if (balanceFactor(node->left) >= 0) // 左子树
        {
            return rightRotate(node);
        }
        else
        {
            // 先左旋再右旋
            node->left = leftRotate(node->left);
            return rightRotate(node);
        }
    }
    else if (bf < -1) // 右子树
    {
        if (balanceFactor(node->right) <= 0) // 右子树
        {
            return leftRotate(node);
        }
        else
        {
            node->right = rightRotate(node->right);
            return leftRotate(node);
        }
    }
    return node;
}
/*********************二叉树平衡化*********************/

// 插入数据，迭代方式 不会选择平衡化
void insertData(DATA_TYPE data)
{
    if (root == NULL)
    {
        root = malloc(sizeof(Node));
        root->data = data;
        root->left = NULL;
        root->right = NULL;
        node_size++;
        return;
    }
    Node *node = root;
    while (node)
    {
        if (data < node->data)
        {
            if (node->left == NULL)
            {
                node->left = malloc(sizeof(Node));
                node->left->data = data;
                node->left->left = NULL;
                node->left->right = NULL;
                break;
            }
            else
            {
                node = node->left;
            }
        }
        else
        {
            if (node->right == NULL)
            {
                node->right = malloc(sizeof(Node));
                node->right->data = data;
                node->right->left = NULL;
                node->right->right = NULL;
                break;
            }
            else
            {
                node = node->right;
            }
        }
    }
    node_size++;
}

// 插入数据：递归方式 平衡化重构
Node *insertNode(Node *T, DATA_TYPE data)
{
    if (root == NULL)
    {
        root = malloc(sizeof(Node));
        root->data = data;
        root->left = NULL;
        root->right = NULL;
        node_size++;
        return root;
    }
    if (T == NULL)
    {
        Node *node = malloc(sizeof(Node));
        node->data = data;
        node->left = NULL;
        node->right = NULL;
        node_size++;
        return node;
    }
    if (data >= T->data)
    {
        T->right = insertNode(T->right, data);
    }
    else
    {
        T->left = insertNode(T->left, data);
    }
    T = rotate(T);
    return T;
}

void insertNode_root(DATA_TYPE data)
{
    root = insertNode(root, data);
}

void preOrder(Node *T)
{
    if (T)
    {
        printf("%d -> ", T->data);
        preOrder(T->left);
        preOrder(T->right);
    }
}
void inOrder(Node *T)
{
    if (T)
    {
        inOrder(T->left);
        printf("%d -> ", T->data);
        inOrder(T->right);
    }
}
void postOrder(Node *T)
{
    if (T)
    {
        postOrder(T->left);
        postOrder(T->right);
        printf("%d -> ", T->data);
    }
}

// 采用逆中序和按层次缩进，是因为把打印结果按顺时针方向旋转90度就能呈现出正常的二叉树形状
void printTree(Node *T, int level)
{
    if (T)
    {
        printTree(T->right, level + 1);
        for (int i = 0; i < level; i++)
        {
            printf("     ");
        }
        printf("%d\n", T->data);
        printTree(T->left, level + 1);
    }
}

int size()
{
    return node_size;
}

int height(Node *T)
{
    if (T == NULL)
    {
        return 0;
    }
    return __max(abs(height(T->left)), abs(height(T->right))) + 1;
}

static void insertToRoot(DATA_TYPE data)
{
    insertNode(root, data);
}

// 左右子树高度差小于等于1
int is_balanced(Node *T)
{
    if (T == NULL)
    {
        return TRUE; // 空树被认为是平衡的
    }
    return abs(height(T->left) - height(T->right)) <= 1 && is_balanced(T->left) && is_balanced(T->right);
}

static int search(Node *T, DATA_TYPE val)
{
    while (T)
    {
        if (T->data == val)
        {
            return TRUE;
        }
        T = (T->data > val) ? T->left : T->right;
    }
    return FALSE;
}

int search_val(DATA_TYPE val)
{
    return search(root, val);
}

Node *getRoot()
{
    return root;
}

/*********************删除元素*********************/
static Node *deleteLeftmost(Node *T)
{
    if (T->left == NULL)
    {
        return T->right;
    }
    else
    {
        T->left = deleteLeftmost(T->left);
        return T;
    }
}

static DATA_TYPE getLeftmost(Node *T)
{
    if (T->left == NULL)
    {
        return T->data;
    }
    else
    {
        return getLeftmost(T->left);
    }
}

static Node *deleteTopmost(Node *T)
{
    if (T->left == NULL)
    {
        return T->right;
    }
    else if (T->right == NULL)
    {
        return T->left;
    }
    else
    {
        T->data = getLeftmost(T->right);
        T->right = deleteLeftmost(T->right);
        return T;
    }
}

static Node *delete(Node *T, DATA_TYPE val)
{
    if (T)
    {
        if (T->data == val)
        {
            node_size--;
            return deleteTopmost(T);
        }
        else if (val < T->data)
        {
            T->left = delete(T->left, val);
        }
        else
        {
            T->right = delete(T->right, val);
        }
    }
    return T;
}

Node *delete_data(DATA_TYPE val)
{
    return delete(root, val);
}

void clear()
{
    free(root);
    root = NULL;
    node_size = 0;
}
/*********************删除元素*********************/

void test_binary_tree()
{
    printf("|***********************基础操作***********************|\n");
    // insertData(4); // root
    // insertData(2); // root left child
    // insertData(1); // 2 left child
    // insertData(3); // 2 right child
    // insertData(6); // root right child
    // insertData(5); // 6 left child
    // insertData(7); // 6 right child

    // insertToRoot(4); // root
    // insertToRoot(2); // root left child
    // insertToRoot(1); // 2 left child
    // insertToRoot(3); // 2 right child
    // insertToRoot(6); // root right child
    // insertToRoot(5); // 6 left child
    // insertToRoot(7); // 6 right child

    insertNode_root(4);
    insertNode_root(2);
    insertNode_root(1);
    insertNode_root(3);
    insertNode_root(6);
    insertNode_root(5);
    insertNode_root(7);

    insertNode_root(8);
    insertNode_root(9);
    insertNode_root(10);
    insertNode_root(11);
    insertNode_root(12);
    // insertNode_root(13);
    printf("逆中序打印：\n");
    printTree(root, 0);

    printf("结点数：%d\n", size());
    printf("是否包含[%d]:%d\n", 3, search_val(3));
    printf("是否包含[%d]:%d\n", 9, search_val(9));

    printf("前序遍历：");
    preOrder(root);
    printf("\n");
    printf("中序遍历：");
    inOrder(root);
    printf("\n");
    printf("后序遍历：");
    postOrder(root);
    printf("\n");
    printf("逆中序打印：\n");
    printTree(root, 0);
    printf("\n");
    int len = height(root);
    printf("二叉树高度：%d\n", len);
    printf("二叉树是否平衡：%d\n", is_balanced(root));

    printf("测试删除元素......");
    printf("\n");
    delete_data(4);
    printf("逆中序打印：\n");
    printTree(root, 0);

    printf("\n");
    delete_data(1);
    printf("逆中序打印：\n");
    printTree(root, 0);

    printf("\n");
    delete_data(5);
    printf("逆中序打印：\n");
    printTree(root, 0);

    clear();

    printf("\n");
    insertNode_root(10);
    insertNode_root(8);
    insertNode_root(15);
    insertNode_root(12);
    insertNode_root(19);
    insertNode_root(13); // 先右旋再左旋
    printf("逆中序打印：\n");
    printTree(root, 0);

    printf("|***********************平衡树***********************|\n");
}

二叉树层序遍历

BinaryTreeLevelOrder.h

#include "BinaryTree.h"

// 辅助队列节点--用于层序遍历
typedef struct QueueNode
{
    Node *data;
    struct QueueNode *next;
} QueueNode;

/********************辅助队列方法********************/
int is_queue_empty();
void enQueue(Node *T);
Node *deQueue();
/********************辅助队列方法********************/

// 二叉树层序遍历
DATA_TYPE **levelOrder(Node *T, int len /* 有多少层 */);

void test_binary_tree_level_order();

BinaryTreeLevelOrder.c

#include <stdio.h>
#include <stdlib.h>

#include "BinaryTreeLevelOrder.h"

// #define col_len (height(getRoot()))

// 层序遍历辅助队列结点数
static int queue_node_size = 0;
static QueueNode *Q = NULL;

// 存储二维数组每行有多少个列 即表示二叉树每一层有多少个节点
static int *col;
static int col_len = 0;

/********************辅助队列方法********************/
int is_queue_empty()
{
    return queue_node_size == 0 || Q == NULL;
}
void enQueue(Node *T)
{
    if (Q == NULL)
    {
        Q = malloc(sizeof(QueueNode));
        Q->data = T;
        Q->next = NULL;
        queue_node_size++;
        return;
    }
    QueueNode *q_node = Q;
    while (q_node->next != NULL)
    {
        q_node = q_node->next;
    }
    q_node->next = malloc(sizeof(QueueNode));
    q_node->next->data = T;
    q_node->next->next = NULL;
    queue_node_size++;
}
Node *deQueue()
{
    Node *val = Q->data;
    Q = Q->next;
    queue_node_size--;
    return val;
}
/********************辅助队列方法********************/

DATA_TYPE **levelOrder(Node *T, int len /* 有多少层 */)
{
    // int (*arr)[MAX_LINE] = malloc(sizeof(*arr) * MAX_LINE);
    // DATA_TYPE *arr;
    DATA_TYPE **arr = malloc(sizeof(DATA_TYPE *) * len);
    col = malloc(sizeof(int) * len);
    enQueue(T);
    while (!is_queue_empty())
    {
        int curr_queue_size = queue_node_size; // 每行节点个数
        DATA_TYPE *per_line = malloc(sizeof(DATA_TYPE) * curr_queue_size);
        int index = 0;
        for (int i = 0; i < curr_queue_size; i++)
        {
            Node *n = deQueue();
            per_line[index++] = n->data;
            // 从左到右收集节点
            if (n->left)
            {
                enQueue(n->left);
            }
            if (n->right)
            {
                enQueue(n->right);
            }
        }
        col[col_len] = index; // 每行有多少列
        arr[col_len] = per_line;
        col_len++;
    }
    return arr;
}

void test_binary_tree_level_order()
{
    printf("|***********************层序遍历***********************|\n");
    Node *root = getRoot();
    int len = height(root);
    DATA_TYPE **arr = levelOrder(root, len); // 锯齿形数组 需要额外数据结构（数组或链表）保存每行列数

    // col_len 等于 len 即二叉树的高度 即二叉树有几行
    for (int i = 0; i < col_len; i++)
    {
        printf("第%d行有结点数: %d\t", i + 1, col[i]);
    }
    printf("\n");

    for (int i = 0; i < len; i++)
    {
        int c = col[i];
        for (int j = 0; j < c; j++)
        {
            int x = arr[i][j];
            printf("arr[%d][%d] = %d\t", i, j, x);
        }
        printf("\n");
    }
}

二叉树非递归遍历

BinaryTreeNonRecursiveOrder.h

#include "BinaryTree.h"

// 辅助队列节点--用于层序遍历
typedef struct StackNode
{
    Node *data;
    struct StackNode *next;
} StackNode;

/********************辅助队列方法********************/
int is_stack_empty();
void push(Node *T);
Node *pop();
/********************辅助队列方法********************/

// 非递归前序遍历
DATA_TYPE *non_recursive_pre_order(Node *root, int node_size);
// 非递归中序遍历
DATA_TYPE *non_recursive_in_order(Node *root, int node_size);
// 非递归后序遍历
DATA_TYPE *non_recursive_post_order(Node *root, int node_size);

void test_binary_tree_non_recursive_order();

BinaryTreeNonRecursiveOrder.c

#include <stdio.h>
#include <stdlib.h>

#include "BinaryTreeNonRecursiveOrder.h"

static int stack_size = 0;
static StackNode *head = NULL;

/********************辅助栈方法********************/

static StackNode *newStackNode(Node *T)
{
    StackNode *node = malloc(sizeof(StackNode));
    node->data = T;
    node->next = NULL;
    return node;
}

int is_stack_empty()
{
    return stack_size == 0;
}
void push(Node *T)
{
    if (head == NULL)
    {
        head = newStackNode(T);
        stack_size++;
        return;
    }
    StackNode *node = newStackNode(T);
    node->next = head;
    head = node;
    stack_size++;
}
Node *pop()
{
    Node *node = head->data;
    head = head->next;
    stack_size--;
    return node;
}
/********************辅助栈方法********************/

DATA_TYPE *non_recursive_pre_order(Node *root, int node_size)
{
    if (root == NULL)
    {
        return NULL;
    }
    DATA_TYPE *result = malloc(sizeof(DATA_TYPE) * node_size);
    DATA_TYPE *p = result;
    while (root || !is_stack_empty())
    {
        if (root)
        {
            *p++ = root->data;
            push(root);
            root = root->left;
        }
        else
        {
            root = pop();
            root = root->right;
        }
    }
    return result;
}
DATA_TYPE *non_recursive_in_order(Node *root, int node_size)
{
    if (root == NULL)
    {
        return NULL;
    }
    DATA_TYPE *result = malloc(sizeof(DATA_TYPE) * node_size);
    DATA_TYPE *p = result;
    while (root || !is_stack_empty())
    {
        if (root)
        {
            push(root);
            root = root->left;
        }
        else
        {
            root = pop();
            *p++ = root->data;
            root = root->right;
        }
    }
    return result;
}

// 非递归后序遍历
DATA_TYPE *non_recursive_post_order(Node *root, int node_size)
{
    if (root == NULL)
    {
        return NULL;
    }
    DATA_TYPE *result = malloc(sizeof(DATA_TYPE) * node_size);
    DATA_TYPE *p = result;
    Node *pre = NULL;
    while (root || !is_stack_empty())
    {
        while (root)
        {
            push(root);
            root = root->left;
        }
        root = pop();
        if (root->right == NULL || root->right == pre)
        {
            *p++ = root->data;
            pre = root;
            root = NULL;
        }
        else
        {
            push(root);
            root = root->right;
        }
    }
    return result;
}

static void printArray(DATA_TYPE *arr, int len)
{
    for (int i = 0; i < len; i++)
    {
        printf("%d -> ", *arr++);
    }
    printf("\n");
}

void test_binary_tree_non_recursive_order()
{
    printf("|***********************二叉树非递归遍历***********************|\n");
    Node *root = getRoot();
    int len = size(root); // 二叉树结点数 用于动态内存分配时计算长度

    DATA_TYPE *arr = non_recursive_post_order(root, len);
    printf("非递归后序遍历：");
    printArray(arr, len);

    arr = non_recursive_in_order(root, len);
    printf("非递归中序遍历：");
    printArray(arr, len);
    
    arr = non_recursive_pre_order(root, len);
    printf("非递归前序遍历：");
    printArray(arr, len);
}