一、实验内容

（一） 某地区35个城市2004年的7项经济统计指标数据见（数据中的“题目1”sheet）。

（1）试用最短距离聚类法对35个城市综合实力进行系统聚类分析，并画出聚类谱系图:

在此次实验内容中我们直接使用SPSS软件用以完成对35个城市综合实例的系统聚类分析并画出聚类谱系图，首先我们在SPSS软件中打开相应的Excel文件，选择SPSS主菜单中的【分析】—>【分类】—>【系统聚类】,打开参数框如下图所示，我们首先逐一添加变量，随后调整【图】与【方法】中的相关参数如下图所示：

调整完毕后点击【确认】，即可得到聚类谱系图结果如下图所示：

（2）试用主成分分析法对35个城市7项经济指标进行主成分分析，并分析其综合实力；

利用主成分分析法对经济指标进行主成分分析，我们首先选择SPSS主菜单中的【分析】—>【降维】—>【因子分析】，打开参数框如下所示，我们首先逐一添加变量，并分别修改【描述】、【提取】与【得分】中的具体参数如下图所示：

调整完毕后点击【确定】即可得到结果，我们主要分析如下所示的总方差解释表格，通过观察表格可得：第一个主成分的初始特征值为3.252，第二个为1.992，第三个为0.988，且前三个主成分累积解释了89.026%的总方差，因此我们可以使用前三个主成分来代表最初的7个指标，用于分析城市的综合实力：

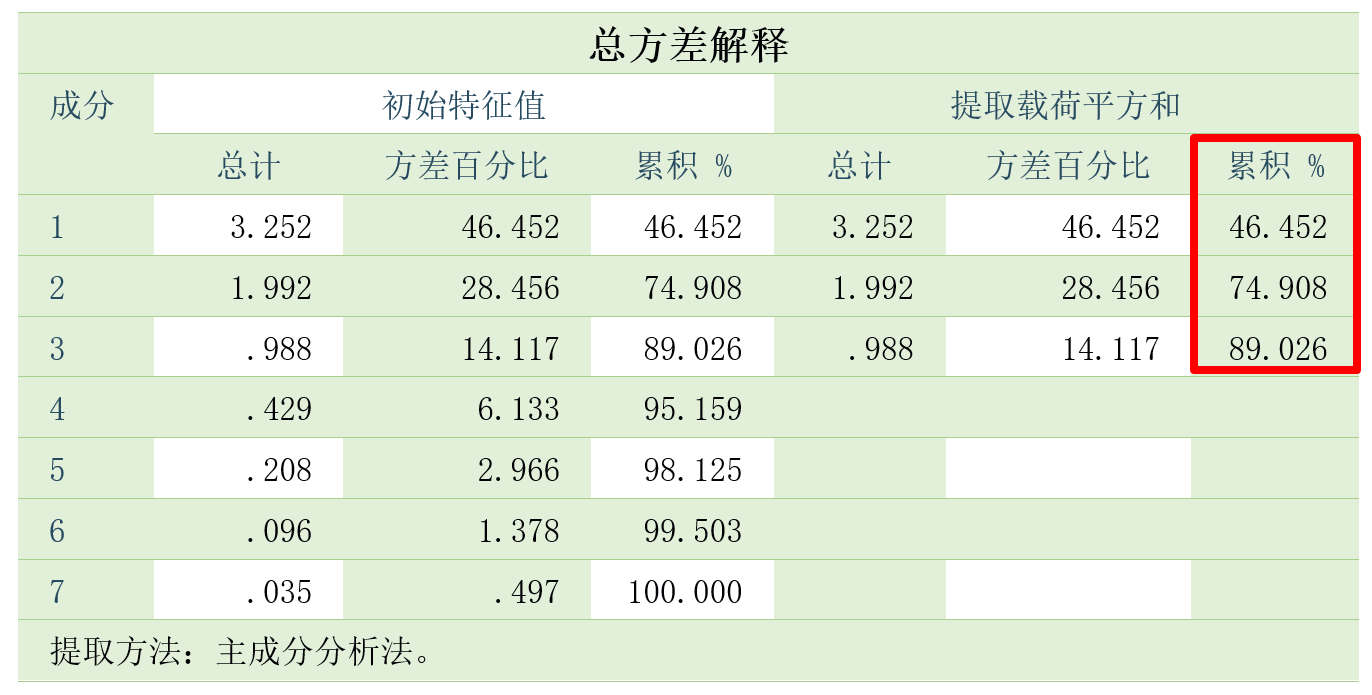
而分析如下所示的成分矩阵与成分得分系数矩阵我们可以识别得到哪些参数与我们计算得到的前三个主成分具有强相关性，比如：第一主成分主要与工业总产值、地方财政预算内收入、城乡居民年底储蓄余额正相关；第二主成分主要与总人口、农业总产值呈现出较强的正相关，而与非农业人口比例呈现较强的负相关；第三主成分则与在岗职工工资总额呈现出极强的正相关，得分系数高达0.995：

得到以上数据，我们即可计算得到每个城市前三项主成分的具体数值，此步骤SPSS已帮我们自动计算得到，但各个城市的综合得分Score=w1*F1+w2*F2+w3*F3，w表示总方差解释中的方差百分比，因此我们可以得到Score=0.46452*F1+0.28456*F2+0.14117*F3，在SPSS的主菜单中点击【转换】—>【计算变量】，在打开的参数框中输入公式如下所示：

我们即可得到35个城市进行主成分分析后的综合实力得分如下图所示：

（3）以第一，二，三主成分为变量，进行聚类分析，结果又怎样呢？

重复上述实验中的第一部分内容，我们选择SPSS主菜单中的【分析】—>【分类】—>【系统聚类】,打开参数框如下图所示，我们逐一添加在上述实验过程中生成的三个主成分变量，随后调整【图】与【方法】中的相关参数如下图所示：

调整完毕后点击【确认】，即可得到聚类谱系图结果如下图所示，其中左图为最短距离聚类法得到的聚类结果，右图为使用主成分分析结果进行聚类得到的聚类结果，可以明显看到由于主成分分析实现了数据的降维和简化，聚类分析的结果中的分支更少，谱系图也得到了一定程度上的简化，这有利于帮助我们更清晰地识别主要的聚类模式和趋势，同时减少了不必要的复杂性，更容易理解数据的结构和特征：

（二）教材P164的上海市部分街道的邻居关系相关数据见实验数据中的“上海市部分街道邻居关系”和“上海市部分街道人口密度”sheet。其文本文件对应的2个txt文件。

首先为了显示我们的局部莫兰指数数据，需要我们在界面中设计一个框体如下图所示，需要特别注意的是，由于局部莫兰指数数量很多，我们需要为其设计一个垂直方向的滚动条：

接下来，在Data文件中我们编写计算局部莫兰指数的代码如下图所示，该代码中我们延续了老师提供的全局莫兰指数的计算方法，主要不同点在于：全局莫兰指数计算的是整个数据集，而我们局部莫兰指数只计算指定节点及其邻域内的数据即可。

分子部分：首先从邻接矩阵 w 中获取节点i与节点j之间的权重，然后乘以节点j的值与数据集均值之间的差值，然后将该结果与节点i的值与数据集均值之间的差值相乘，即可得到分子；分母部分：同计算全局莫兰指数相同，直接调用了SST()方法即可得到结果：

最后在Form1.cs的代码文件中，我们添加调用localMoran()函数的代码如下所示，并将其结果与我们创建的框体LocalMoranValues绑定起来：

最后运行代码，分别输入邻接矩阵与上海市街道人口密度，即可得到结果如下所示：

二、实验心得

此次实验中的两个任务，重点内容分别为学习使用SPSS软件进行聚类分析与在C#环境下计算莫兰指数，前者因为在以往的学习过程中经常使用到SPSS软件进行数据分析因此内容推进的较快，而后者因为对在VS软件中进行界面设计不够熟悉因此推进较慢，也存在一些问题与困难目前尚未解决，对软件的许多功能尚不熟悉，需要课后的不断钻研补充。

在实验过程中我发现，代码编写的核心与诀窍在于是否对相关计算公式了解透彻，以此次实验的全局莫兰指数与局部莫兰指数代码编写为例，当我已经充分理解全局与局部莫兰指数的区别（核心区别在于数据集对象分别为整体数据集与邻域数据集）后，Data部分的代码编写其实非常之快，主要是在界面设计时耗费了比较多的时间，因此在实验课课下还需要花费一定的时间多去了解该如何在VS环境下进行界面设计。