ABB工业机器人(IRB2600)如下图所示(d1=444.8mm,a1=150mm,a2=700mm,a3=115mm,d4=795mm,d6=85mm),利用改进DH法建模,坐标系如下所示:

利用改进DH法建模,该机器人的DH参数表如下所示:

对该机械臂进行位置分析,即给定一组关节角度,求解末端点P相对于基坐标系的坐标值以及末端坐标系相对于基坐标系的姿态矩阵。
1.1 机器人工具箱仿真(RT)
当 θ 1 = 10 ° \theta_1=10° θ1=10°, θ 2 = 30 ° \theta_2=30° θ2=30°, θ 3 = 50 ° \theta_3=50° θ3=50°, θ 4 = 70 ° \theta_4=70° θ4=70°, θ 5 = 90 ° \theta_5=90° θ5=90°, θ 6 = 110 ° \theta_6=110° θ6=110°时,利用机器人工具箱的MDH法建模仿真如下:

仿真结果如下:

此时,末端点P的位置坐标仿真值为:
x
P
=
0.697824163926912
m
x_P=0.697824163926912\ m
xP=0.697824163926912 m,
y
P
=
0.204151283892428
m
y_P=0.204151283892428\ m
yP=0.204151283892428 m,
z
P
=
0.283016909593919
m
z_P=0.283016909593919\ m
zP=0.283016909593919 m
末端坐标系相对于基坐标系的旋转矩阵为:
R
=
[
−
0.859075284270241
0.130692715335043
−
0.494882885251004
−
0.477829973409708
0.141827001123388
0.866927689178068
0.183488889220255
0.981226026922798
−
0.059391174613885
]
R = \begin{bmatrix} -0.859075284270241 \,\,\, 0.130692715335043 \,\,\, -0.494882885251004 \\ -0.477829973409708\,\,\,\,\, 0.141827001123388 \,\,\,\,\,\, 0.866927689178068 \\ 0.183488889220255\,\,\,\, 0.981226026922798\, -0.059391174613885 \end{bmatrix}
R=
−0.8590752842702410.130692715335043−0.494882885251004−0.4778299734097080.1418270011233880.8669276891780680.1834888892202550.981226026922798−0.059391174613885
1.2 改进DH法建模仿真(MDH)
MDH的齐次变换矩阵如下:

坐标系6的齐次变换矩阵为:

当
θ
1
=
10
°
\theta_1=10°
θ1=10°,
θ
2
=
30
°
\theta_2=30°
θ2=30°,
θ
3
=
50
°
\theta_3=50°
θ3=50°,
θ
4
=
70
°
\theta_4=70°
θ4=70°,
θ
5
=
90
°
\theta_5=90°
θ5=90°,
θ
6
=
110
°
\theta_6=110°
θ6=110°时,计算结果如下:

此时,末端点P的位置坐标如下所示: x P = 0.697824163926912 m x_P=0.697824163926912\ m xP=0.697824163926912 m, y P = 0.204151283892428 m y_P=0.204151283892428\ m yP=0.204151283892428 m, z P = 0.283016909593919 m z_P=0.283016909593919\ m zP=0.283016909593919 m
末端坐标系相对于基坐标系的旋转矩阵为:
R = [ − 0.859075284270241 0.130692715335043 − 0.494882885251004 − 0.477829973409708 0.141827001123388 0.866927689178068 0.183488889220255 0.981226026922798 − 0.059391174613885 ] R = \begin{bmatrix} -0.859075284270241 \,\,\, 0.130692715335043 \,\,\, -0.494882885251004 \\ -0.477829973409708\,\,\,\,\, 0.141827001123388 \,\,\,\,\,\, 0.866927689178068 \\ 0.183488889220255\,\,\,\, 0.981226026922798\, -0.059391174613885 \end{bmatrix} R= −0.8590752842702410.130692715335043−0.494882885251004−0.4778299734097080.1418270011233880.8669276891780680.1834888892202550.981226026922798−0.059391174613885
1.3 Simscape模型仿真(Sim)
首先将solidworks模型的零件导出step格式,注意要选择参考坐标系。然后,在simscape模块中选择multibody模型进行建模,具体如下所示:

当设置好角度时,进行仿真,结果如下所示:

当 θ 1 = 10 ° \theta_1=10° θ1=10°, θ 2 = 30 ° \theta_2=30° θ2=30°, θ 3 = 50 ° \theta_3=50° θ3=50°, θ 4 = 70 ° \theta_4=70° θ4=70°, θ 5 = 90 ° \theta_5=90° θ5=90°, θ 6 = 110 ° \theta_6=110° θ6=110°时,计算结果如下:
末端点P的位置坐标可以获得,具体值如下所示: x P = 0.69782416392691 m x_P=0.69782416392691\ m xP=0.69782416392691 m, y P = 0.20415128389243 m y_P=0.20415128389243\ m yP=0.20415128389243 m, z P = 0.28301690959392 m z_P=0.28301690959392\ m zP=0.28301690959392 m
末端坐标系相对于基坐标系的旋转矩阵为:
R = [ − 0.85907528427024 0.13069271533504 − 0.49488288525101 − 0.47782997340971 0.14182700112339 0.86692768917807 0.18348888922026 0.9812260269228 − 0.059391174613883 ] R = \begin{bmatrix} -0.85907528427024 \,\,\, 0.13069271533504 \,\,\, -0.49488288525101 \\ -0.47782997340971\,\,\,\,\, 0.14182700112339 \,\,\,\,\,\, 0.86692768917807 \\ 0.18348888922026\,\,\,\, 0.9812260269228\, -0.059391174613883 \end{bmatrix} R= −0.859075284270240.13069271533504−0.49488288525101−0.477829973409710.141827001123390.866927689178070.183488889220260.9812260269228−0.059391174613883
1.4 结论
通过几种方法进行位置分析,可以看出:当给定某一关节角度时,不同方法计算出来的末端点P的坐标值以及末端坐标系相对于基坐标系的旋转矩阵几乎一样,,表明计算成功!!
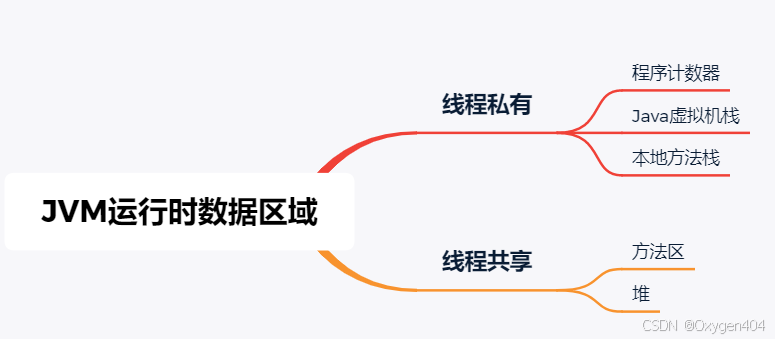













![[LeetCode]day9 203.移除链表元素](https://i-blog.csdnimg.cn/img_convert/4b4986b75666216401a7e6888726f676.jpeg)



