【LeetCode】906、超级回文数

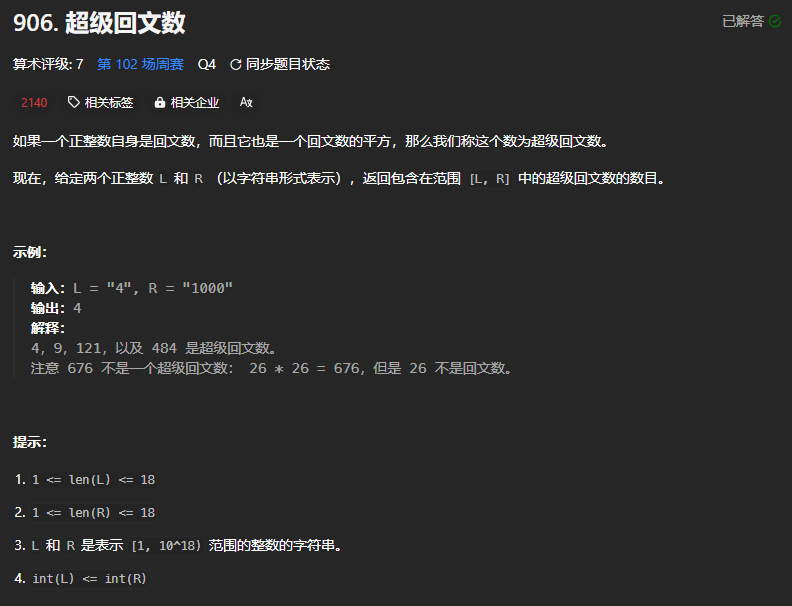
一、通过数据量猜解法 枚举 数学 回文

1.1 通过数据量猜解法 枚举 数学 回文

减小数据规模: 先构成回文, 再平方, 再判断是否是范围内的回文数
缩小数据范围: 回文种子 => 回文数(即根号) => 数字(即根号的平方)

// go
func superpalindromesInRange(left string, right string) (ans int) {
    l, _ := strconv.Atoi(left)
    r, _ := strconv.Atoi(right) // 规模为10^18, 的数字
    limit := int(math.Sqrt(float64(r))) // 规模为10^9, 的数字的根号
    seed := 1 // 规模10^5, 的原初种子, 通过 回文 可构成 数字的根号
    num := 0
    for num <= limit {
        // 原初种子 组成 偶数回文串
        num = evenEnlarge(seed)
        if isPalidromInRange(num*num, l, r) {ans++}

        // 原初种子 组成 奇数回文串
        num = oddEnlarge(seed)
        if isPalidromInRange(num*num, l, r) {ans++}

        // 原初种子 变大 继续后续遍历
        seed++
    }
    return
}

// 是否是范围内的回文数
func isPalidromInRange(num, l, r int) bool {
    return num >= l && num <= r && isPalinrome(num)
}

// 把数字x变为偶数回文串, 如123变为123321
func evenEnlarge(x int) int {
    ans := x
    for x > 0 {
        ans = ans * 10 + x % 10
        x /= 10
    }
    return ans
}


// 把数字x变为奇数回文串, 如123变为12321
func oddEnlarge(x int) int {
    ans := x
    x /= 10 // x 先除以10, 如 123 变为 12
    for x > 0 {
        ans = ans * 10 + x % 10
        x /= 10
    }
    return ans
}

// 数字x是否为回文数
func isPalinrome(x int) bool {
    if x < 0 {return false}
    offset := 1
    for x / offset >= 10 {
        offset *= 10
    }

    for x != 0 {
        if x/offset != x%10 {return false}
        x = (x%offset)/10
        offset /= 100
    }
    return true
}

参考左神 根据数据量猜解法

1.2 多语言解法

$Cpp/Go/Python/Rust/Js/Ts$

// cpp

// go 同上

# python

// rust

// js

// ts

二、打表法

先算出所有 0 到 10^18 范围内的 超级回文数, 因为总共只有84个数, 非常少, 所以可以提前存储好, 得到一个数组. PS: 此计算过程因为是单独准备的, 所以并不算在题目时间里

然后遍历每个提前存储好的数字, 判断是否 在 [l, r] 范围内即可

func superpalindromesInRange(left string, right string) (ans int) {
    // helper()
    arr := []int{121 ,
        1 ,
        484 ,
        4 ,
        9 ,
        1002001 ,
        10201 ,
        1234321 ,
        12321 ,
        14641 ,
        4008004 ,
        40804 ,
        44944 ,
        10000200001 ,
        100020001 ,
        10221412201 ,
        102030201 ,
        104060401 ,
        12102420121 ,
        121242121 ,
        12345654321 ,
        123454321 ,
        125686521 ,
        40000800004 ,
        400080004 ,
        404090404 ,
        100000020000001 ,
        1000002000001 ,
        100220141022001 ,
        1002003002001 ,
        1004006004001 ,
        102012040210201 ,
        1020304030201 ,
        102234363432201 ,
        1022325232201 ,
        1024348434201 ,
        121000242000121 ,
        1210024200121 ,
        121242363242121 ,
        1212225222121 ,
        1214428244121 ,
        123212464212321 ,
        1232346432321 ,
        123456787654321 ,
        1234567654321 ,
        400000080000004 ,
        4000008000004 ,
        4004009004004 ,
        1000000002000000001 ,
        10000000200000001 ,
        1000220014100220001 ,
        10002000300020001 ,
        10004000600040001 ,
        1002003004003002001 ,
        10020210401202001 ,
        1002223236323222001 ,
        10022212521222001 ,
        10024214841242001 ,
        1020100204020010201 ,
        10201020402010201 ,
        1020322416142230201 ,
        10203040504030201 ,
        10205060806050201 ,
        1022123226223212201 ,
        10221432623412201 ,
        1022345658565432201 ,
        10223454745432201 ,
        1210000024200000121 ,
        12100002420000121 ,
        1210242036302420121 ,
        12102202520220121 ,
        12104402820440121 ,
        1212203226223022121 ,
        12122232623222121 ,
        1212445458545442121 ,
        12124434743442121 ,
        1232100246420012321 ,
        12321024642012321 ,
        1232344458544432321 ,
        12323244744232321 ,
        1234323468643234321 ,
        12343456865434321 ,
        12345678987654321 ,
        4000000008000000004 ,
        40000000800000004 ,
        40004000900040004}
    l, _ := strconv.Atoi(left)
    r, _ := strconv.Atoi(right)
    for _, v := range arr {
        if v >= l && v <= r {ans++}
    }
    return
}

func helper() {
    limit := int(1e9)
    seed := 1 // 规模10^5, 的原初种子, 通过 回文 可构成 数字的根号
    num := 0
    for num <= limit {
        // 原初种子 组成 偶数回文串
        num = evenEnlarge(seed)
        if isPalidromInRange(num*num) {fmt.Println(num*num, ",")}

        // 原初种子 组成 奇数回文串
        num = oddEnlarge(seed)
        if isPalidromInRange(num*num) {fmt.Println(num*num, ",")}

        // 原初种子 变大 继续后续遍历
        seed++
    }
}

// 是否是范围内的回文数
func isPalidromInRange(num int) bool {
    return isPalinrome(num)
}

// 把数字x变为偶数回文串, 如123变为123321
func evenEnlarge(x int) int {
    ans := x
    for x > 0 {
        ans = ans * 10 + x % 10
        x /= 10
    }
    return ans
}


// 把数字x变为奇数回文串, 如123变为12321
func oddEnlarge(x int) int {
    ans := x
    x /= 10 // x 先除以10, 如 123 变为 12
    for x > 0 {
        ans = ans * 10 + x % 10
        x /= 10
    }
    return ans
}

// 数字x是否为回文数
func isPalinrome(x int) bool {
    if x < 0 {return false}
    offset := 1
    for x / offset >= 10 {
        offset *= 10
    }

    for x != 0 {
        if x/offset != x%10 {return false}
        x = (x%offset)/10
        offset /= 100
    }
    return true
}

参考左神 根据数据量猜解法