高阶数据结构--图（graph）

news2024/11/5 12:23:35

图（graph）

  • 1.并查集
    • 1. 并查集原理
    • 2. 并查集实现
    • 3. 并查集应用
  • 2.图的基本概念
  • 3. 图的存储结构
    • 3.1 邻接矩阵
    • 3.2 邻接矩阵的代码实现
    • 3.3 邻接表
    • 3.4 邻接表的代码实现
  • 4. 图的遍历
    • 4.1 图的广度优先遍历
    • 4.2 广度优先遍历的代码

1.并查集

1. 并查集原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find
set)。

比如：某公司今年校招全国总共招生10人，西安招4人，成都招3人，武汉招3人，10个人来自不
同的学校，起先互不相识，每个学生都是一个独立的小团体，现给这些学生进行编号：{0, 1, 2, 3,4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体，数组中的数字代表：该小集体中具有成员的个
数。(负号下文解释)
在这里插入图片描述
毕业后，学生们要去公司上班，每个地方的学生自发组织成小分队一起上路，于是：

西安学生小分队s1={0,6,7,8}，成都学生小分队s2={1,4,9}，武汉学生小分队s3={2,3,5}就相互认识了，10个人形成了三个小团体。假设右三个群主0,1,2担任队长，负责大家的出行。
在这里插入图片描述
一趟火车之旅后，每个小分队成员就互相熟悉，称为了一个朋友圈。
在这里插入图片描述
从上图可以看出：编号6,7,8同学属于0号小分队，该小分队中有4人(包含队长0)；编号为4和9的同学属于1号小分队，该小分队有3人(包含队长1)，编号为3和5的同学属于2号小分队，该小分队有3个人(包含队长1)。
仔细观察数组中内融化，可以得出以下结论：

  1. 数组的下标对应集合中元素的编号
  2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
  3. 数组中如果为非负数，代表该元素双亲在数组中的下标

在公司工作一段时间后，西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起，两个
小圈子的学生相互介绍，最后成为了一个小圈子：

在这里插入图片描述
现在0集合有7个人，2集合有3个人，总共两个朋友圈。
通过以上例子可知，并查集一般可以解决一下问题：

  1. 查找元素属于哪个集合
    沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)
  2. 查看两个元素是否属于同一个集合
    沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在
  3. 将两个集合归并成一个集合
    -将两个集合中的元素合并
    -将一个集合名称改成另一个集合的名称
  4. 集合的个数
    遍历数组，数组中元素为负数的个数即为集合的个数。

2. 并查集实现

template<class T>
class UnionFindSet
{
public:
	UnionFindSet(size_t n):
	_ufs(n,-1)
	{}

	int Find(int x)//查找根
	{
		int root = x;
		while (_ufs[root] >= 0)
		{
			root = _ufs[root];
		}

		return root;
	}

	void Union(int x1, int x2)
	{
		int x = Find(x1);
		int y = Find(x2);

		if (x == y)
			return;//本来就在一个团体

		_ufs[x] += _ufs[y];
		_ufs[y] = x;
	}

	bool Inset(int x1, int x2)
	{
		return Find(x1) == Find(x2);
	}

	size_t SetSize()
	{
		size_t size = 0;
		for (size_t i = 0; i < _ufs.size(); i++)
		{
			if (_ufs[i] < 0)
				size++;
		}

		return size;
	}

private:
	vector<T> _ufs;
};

此外为了学习图这个非常难得数据结构我这里补充一下通过编号找名字，通过名字找编号如何实现：

//template<class T>
//class UnionFindSet
//{
//public:
//
//	UnionFindSet(const T* a, const size_t n)
//	{
//		for (size_t i = 0; i < n; i++)
//		{
//			_a.push_back(a[i]);
//			_indexMap[a[i]] = i;
//		}
//	}
//
//private:
//	vector<T> _a;//编号找名字
//	map<T, int> _indexMap;//名字找编号
//};

实现后的效果如图：
在这里插入图片描述
将以上内容理解清楚我们才能进入更好地进入图的学习。

3. 并查集应用

https://leetcode.cn/problems/bLyHh0/

https://leetcode-cn.com/problems/satisfiability-of-equality-equations/comments/

以上两个题就是并查集能解决的问题，由于我们主要的目标是学习图，所以需要答案可以私信我

2.图的基本概念

图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E)，其中：
顶点集合V = {x|x属于某个数据对象集}是有穷非空集合；

E = {(x,y)|x,y属于V}或者E = {<x, y>|x,y属于V && Path(x, y)}是顶点间关系的有穷集合，也叫
做边的集合。

(x, y)表示x到y的一条双向通路，即(x, y)是无方向的；Path(x, y)表示从x到y的一条单向通路，即
Path(x, y)是有方向的。

顶点和边：图中结点称为顶点，第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间
有一条边，图中的第k条边记作ek，ek = (vi，vj)或<vi，vj>。

有向图和无向图：在有向图中，顶点对<x, y>是有序的，顶点对<x，y>称为顶点x到顶点y的一条
边(弧)，<x, y>和<y, x>是两条不同的边，比如下图G3和G4为有向图。在无向图中，顶点对(x, y)
是无序的，顶点对(x,y)称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x, y)和(y，x)
是同一条边，比如下图G1和G2为无向图。注意：无向边(x, y)等于有向边<x, y>和<y, x>。

在这里插入图片描述
完全图：在有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边，
则称此图为无向完全图，比如上图G1；在n个顶点的有向图中，若有n * (n-1)条边，即任意两个
顶点之间有且仅有方向相反的边，则称此图为有向完全图，比如上图G4。

邻接顶点：在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u,v)依附于顶点u和v；在有向图G中，若<u, v>是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边<u, v>与顶点u和顶点v相关联。

顶点的度：顶点v的度是指与它相关联的边的条数，记作deg(v)。在有向图中，顶点的度等于该顶点的入度与出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v);顶点v的出度是以v为起始点的有向边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。注
意：对于无向图，顶点的度等于该顶点的入度和出度，即dev(v) = indev(v) = outdev(v)。
路径：在图G = (V， E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶
点序列为从顶点vi到顶点vj的路径。

路径长度：对于不带权的图，一条路径的路径长度是指该路径上的边的条数；对于带权的图，一
条路径的路径长度是指该路径上各个边权值的总和。
在这里插入图片描述
简单路径与回路：若路径上各顶点v1，v2，v3，…，vm均不重复，则称这样的路径为简单路
径。若路径上第一个顶点v1和最后一个顶点vm重合，则称这样的路径为回路或环。
在这里插入图片描述
子图：设图G = {V, E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图。
在这里插入图片描述
连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。

强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj
到vi的路径，则称此图是强连通图。

生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点
和n-1条边。

3. 图的存储结构

因为图中既有节点，又有边(节点与节点之间的关系)，因此，在图的存储中，只需要保存：节点和边关系即可。节点保存比较简单，只需要一段连续空间即可，那边关系该怎么保存呢？

3.1 邻接矩阵

因为节点与节点之间的关系就是连通与否，即为0或者1，因此邻接矩阵(二维数组)即是：先用一
个数组将定点保存，然后采用矩阵来表示节点与节点之间的关系。
在这里插入图片描述
注意：

  1. 无向图的邻接矩阵是对称的，第i行(列)元素之和，就是顶点i的度。有向图的邻接矩阵则不一
    定是对称的，第i行(列)元素之后就是顶点i 的出(入)度。
  2. 如果边带有权值，并且两个节点之间是连通的，上图中的边的关系就用权值代替，如果两个
    顶点不通，则使用无穷大代替。
    在这里插入图片描述
  3. 用邻接矩阵存储图的有点是能够快速知道两个顶点是否连通，缺陷是如果顶点比较多，边比
    较少时，矩阵中存储了大量的0成为系数矩阵，比较浪费空间，并且要求两个节点之间的路
    径不是很好求。

3.2 邻接矩阵的代码实现

namespace matrix
{
	template<class V, class W, W MAX = INT_MAX, bool Direction = false>
	class Graph
	{
	public:

		Graph(const V* a, size_t n)
		{
			_vertexs.reserve(n);
			for (size_t i = 0; i < n; i++)
			{
				_vertexs.push_back(a[i]);//存放顶点
				_IndexMap[a[i]] = i;//存放顶点，并建立顶点与下标的映射关系
			}

			_matrix.resize(n);
			for (int i = 0; i < _matrix.size(); i++)
			{
				_matrix[i].resize(n, MAX);
			}
		}

		size_t GetIndexMap(const V& v)
		{
			auto it = _IndexMap.find(v);
			if (it != _IndexMap.end())
				return it->second;
			else
			{
				return -1;
			}
		}

		void AddEdge(const V& src, const V& dst, const W& w)
		{
			size_t srci = GetIndexMap(src);
			size_t dsti = GetIndexMap(dst);

			_matrix[srci][dsti] = w;
			if (Direction == false)
			{
				_matrix[dsti][srci] = w;
			}
		}

		void Print()
		{
			cout <<"  ";
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				printf("%4d", i);
			}
			cout << endl;

			for (size_t i = 0; i < _matrix.size(); i++)
			{
				cout << i << ' ';
				for (size_t j = 0; j < _matrix[i].size(); j++)
				{
					if (_matrix[i][j] == MAX)
						printf("%4c", '&');
					else
						printf("%4d", _matrix[i][j]);
				}
				cout << endl;
			}
		}

	private:
		vector<V> _vertexs;//顶点集
		map<V,int> _IndexMap;//下标和顶点映射关系
		vector<vector<W>> _matrix;//邻接矩阵
	};

	void test1()
	{
		Graph<char, int, INT_MAX, false> g("0123", 4);
		g.AddEdge('0', '0', 1);
		g.AddEdge('1', '1', 2);
		g.AddEdge('2', '2', 3);
		g.AddEdge('3', '3', 4);

		g.Print();
	}
	}

3.3 邻接表

邻接表：使用数组表示顶点的集合，使用链表表示边的关系。

  1. 无向图邻接表存储
    2.
    注意：无向图中同一条边在邻接表中出现了两次。如果想知道顶点vi的度，只需要知道顶点
    vi边链表集合中结点的数目即可。

  2. 有向图邻接表存储
    在这里插入图片描述
    注意：有向图中每条边在邻接表中只出现一次，与顶点vi对应的邻接表所含结点的个数，就
    是该顶点的出度，也称出度表，要得到vi顶点的入度，必须检测其他所有顶点对应的边链
    表，看有多少边顶点的dst取值是i。

3.4 邻接表的代码实现

namespace Link_table
{
	template<class W>
	struct Edge
	{
		W _w;
		//int _srci;
		size_t _dsti;//指向的点
		Edge<W>* _next;

		Edge(size_t dsti,const W& w):
			_dsti(dsti),
			_w(w),
			_next(nullptr)
		{}
	};

	template<class V, class W, bool Direction = false>
	class Graph
	{
		typedef Edge<W> Edge;
	public:

		Graph(const V* a, size_t n)
		{
			_vertexs.reserve(n);
			for (size_t i = 0; i < n; i++)
			{
				_vertexs.push_back(a[i]);//存放顶点
				_IndexMap[a[i]] = i;//存放顶点，并建立顶点与下标的映射关系
			}

			_linktable.resize(n,nullptr);
		}

		size_t GetIndexMap(const V& v)
		{
			auto it = _IndexMap.find(v);
			if (it != _IndexMap.end())
			{
				return it->second;
			}
			else
			{
				return -1;
			}
		}

		void AddEdge(const V& src, const V& dst, const W& w)
		{
			size_t srci = GetIndexMap(src);
			size_t dsti = GetIndexMap(dst);

			Edge* eg = new Edge(dsti, w);
			eg->_next = _linktable[srci];
			_linktable[srci] = eg;

			if (Direction == false)
			{
				Edge* eg = new Edge(srci, w);
				eg->_next = _linktable[dsti];
				_linktable[dsti] = eg;
			}
		}

		void Print()
		{
			for (size_t i = 0; i < _linktable.size(); i++)
			{
				cout << _vertexs[i] << "   ";
				Edge* cur = _linktable[i];
				while (cur)
				{
					cout << _vertexs[cur->_dsti] << ":" << cur->_w << "->";
					cur = cur->_next;
				}
				cout << "nullptr";
				cout << endl;
			}
		}

	private:
		vector<V> _vertexs;//顶点集
		map<V, int> _IndexMap;//下标和顶点映射关系
		vector<Edge*> _linktable;//
	};

	void test1()
	{
		string a[] = { "张三", "李四", "王五", "赵六" };
		Graph<string, int, true> g1(a, 4);
		g1.AddEdge("张三", "李四", 100);
		g1.AddEdge("张三", "王五", 200);
		g1.AddEdge("王五", "赵六", 30);
		g1.Print();
	}

	
}

4. 图的遍历

给定一个图G和其中任意一个顶点v0，从v0出发，沿着图中各边访问图中的所有顶点，且每个顶
点仅被遍历一次。"遍历"即对结点进行某种操作的意思。
请思考树以前是怎么遍历的，此处可以直接用来遍历图吗？为什么？

4.1 图的广度优先遍历

在这里插入图片描述
在这里插入图片描述

4.2 广度优先遍历的代码

namespace matrix
{
	template<class V, class W, W MAX = INT_MAX, bool Direction = false>
	class Graph
	{
	public:

		Graph(const V* a, size_t n)
		{
			_vertexs.reserve(n);
			for (size_t i = 0; i < n; i++)
			{
				_vertexs.push_back(a[i]);//存放顶点
				_IndexMap[a[i]] = i;//存放顶点，并建立顶点与下标的映射关系
			}

			_matrix.resize(n);
			for (int i = 0; i < _matrix.size(); i++)
			{
				_matrix[i].resize(n, MAX);
			}
		}

		size_t GetIndexMap(const V& v)
		{
			auto it = _IndexMap.find(v);
			if (it != _IndexMap.end())
				return it->second;
			else
			{
				return -1;
			}
		}

		void AddEdge(const V& src, const V& dst, const W& w)
		{
			size_t srci = GetIndexMap(src);
			size_t dsti = GetIndexMap(dst);

			_matrix[srci][dsti] = w;
			if (Direction == false)
			{
				_matrix[dsti][srci] = w;
			}
		}

		void BFS(const V& v)
		{
			size_t scr = GetIndexMap(v);
			queue<int> q;

			vector<bool> visited(_vertexs.size(), false);
			visited[scr] = true;
			q.push(scr);
			size_t n = _vertexs.size();
			while (!q.empty())
			{
				size_t front = q.front();
				q.pop();
				cout << front << ":" << _vertexs[front] << endl;
				for (size_t i = 0; i < n; i++)
				{
					if (_matrix[front][i] != MAX)
					{
						if (visited[i] == false)
						{
							q.push(i);
							visited[i] = true;
						}
					}
				}
			}
		}

		void Print()
		{
			cout <<"  ";
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				printf("%4d", i);
			}
			cout << endl;

			for (size_t i = 0; i < _matrix.size(); i++)
			{
				cout << i << ' ';
				for (size_t j = 0; j < _matrix[i].size(); j++)
				{
					if (_matrix[i][j] == MAX)
						printf("%4c", '&');
					else
						printf("%4d", _matrix[i][j]);
				}
				cout << endl;
			}
		}

	private:
		vector<V> _vertexs;//顶点集
		map<V,int> _IndexMap;//下标和顶点映射关系
		vector<vector<W>> _matrix;//邻接矩阵
	};

	void test1()
	{
		Graph<char, int, INT_MAX, false> g("0123", 4);
		g.AddEdge('0', '0', 1);
		g.AddEdge('1', '1', 2);
		g.AddEdge('2', '2', 3);
		g.AddEdge('3', '3', 4);

		g.Print();
	}

	void BDFStest()
	{
		string a[] = { "张三", "李四", "王五", "赵六" };
		Graph<string, int, true> g1(a, 4);
		g1.AddEdge("张三", "李四", 100);
		g1.AddEdge("张三", "王五", 200);
		g1.AddEdge("王五", "赵六", 30);
		g1.Print();

		g1.BFS("张三");
	}
}

效果如下:
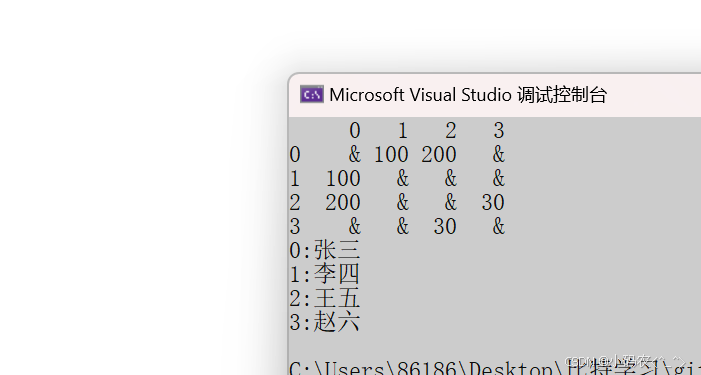
在这里插入图片描述

后面的深度优先遍历下一节继续，原因是因为这一部分挺难的，大家其实需要花很多时间去理解一下，总的来说图需要我们画很多精力去学习，相信学懂这一部分不光在代码能力上有很大提升，在逻辑思维也会有很大提升的。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2229280.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

全渠道供应链打造中企业定制开发2+1链动模式S2B2C商城小程序的策略与影响

全渠道供应链打造中企业定制开发2+1链动模式S2B2C商城小程序的策略与影响

摘要&#xff1a;本文探讨了全渠道供应链打造对于零售企业的重要性及面临的挑战&#xff0c;着重分析了物流环节整合的难点&#xff0c;并以家电行业为例说明了节假日期间物流对企业经营的影响。同时&#xff0c;引入“企业定制开发21链动模式S2B2C商城小程序”这一关键因素&am…
阅读更多...
Oracle视频基础1.3.3练习

Oracle视频基础1.3.3练习

1.3.3 检查数据库启动情况 ps -ef | grep oracle启动数据库 sqlplus /nolog conn / as sysdba修改 fast_start_mttr_target 参数为初始值-50&#xff0c;缺省 scope 和 sid&#xff0c;查看修改结果 show parameter fast; alter system set parameter 250; show parameter fa…
阅读更多...
ArcGIS005:ArcMap常用操作101-150例动图演示

ArcGIS005:ArcMap常用操作101-150例动图演示

摘要&#xff1a;本文涵盖了GIS软件操作的多方面内容&#xff0c;包括地图文档的新建、打开、保存及版本兼容性处理&#xff1b;错误与警告的查阅及帮助文档的使用技巧&#xff1b;地图打印比例尺的调整与地图信息的完善&#xff1b;图层操作的撤销与恢复&#xff0c;界面元素的…
阅读更多...
电商预售是时候“消亡”了

电商预售是时候“消亡”了

淘天反复横跳在预售里。 作者|周立青 编辑|杨舟 “明知道搞复杂的预售规则会给用户体验带来伤害&#xff0c;弊大于利&#xff0c;甚至内网就有很多人在骂在批评&#xff0c;还要在今年双11这么玩&#xff0c;算是见识到了公司的组织惯性和路径依赖是多么可怕”&#xff0c;淘…
阅读更多...
关于游戏加加不可以在cs2中显示的解决方案

关于游戏加加不可以在cs2中显示的解决方案

输入的代码如下 -allow_third_party_software 1.打开steam 右键cs2&#xff0c;打开属性。 然后再这里填上这个代码就可以了
阅读更多...
Codeforces Global Round 27 D.Yet Another Real Number Problem

Codeforces Global Round 27 D.Yet Another Real Number Problem

题目 题解&#xff1a; #include <bits/stdc.h> using namespace std; // #define int long long #define pb push_back #define fi first #define se second #define lson p << 1 #define rson p << 1 | 1 #define ll long long #define pii pair<int, i…
阅读更多...
Spring Boot中解决BeanDefinitionStoreException问题的实战分享

Spring Boot中解决BeanDefinitionStoreException问题的实战分享

目录 前言1. 问题背景2. 问题分析2.1 异常分析2.2 常见的错误原因2.3 排查过程 3. 解决方案3.1 清理缓存和重建项目3.1.1 清理IDEA缓存3.1.2 使用Maven清理并重建项目 3.2 升级Maven版本3.2.1 下载最新Maven版本3.2.2 IDEA配置新的Maven版本3.2.3 清理缓存并重新构建 3.3 验证问…
阅读更多...
新160个crackme - 088-[KFC]fish‘s CrackMe

新160个crackme - 088-[KFC]fish‘s CrackMe

运行分析 需破解用户名和RegKey PE分析 C程序&#xff0c;32位&#xff0c;无壳 静态分析&动态调试 ida函数窗口逐个查看&#xff0c;找到关键函数sub_401440 ida无法动调&#xff0c;需使用OD&#xff0c;启用StrongOD插件才可以动调ida静态分析&#xff0c;逻辑如下&…
阅读更多...
淘宝/天猫获得淘宝商品评论 API 返回值说明

淘宝/天猫获得淘宝商品评论 API 返回值说明

淘宝/天猫获得淘宝商品评论 API 返回值说明 item_review-获得淘宝商品评论API注册测试 taobao.item_review 公共参数 名称类型必须描述keyString是调用key&#xff08;必须以GET方式拼接在URL中&#xff09;secretString是调用密钥api_nameString是API接口名称&#xff08;包…
阅读更多...
Rust精简核心笔记：第三波，基础语法完结篇

Rust精简核心笔记：第三波，基础语法完结篇

今天是Rust精简核心笔记第三波&#xff0c;也是完结篇。之前已经介绍了二波&#xff0c;Rust精简核心笔记&#xff1a;第一波&#xff0c;深入浅出语法精华-CSDN博客&#xff0c;Rust精简核心笔记&#xff1a;第二波&#xff0c;语法精髓部分解锁-CSDN博客&#xff0c;通过三波…
阅读更多...
如何找到车在路上行驶的视频素材

如何找到车在路上行驶的视频素材

作为一名热爱拍摄视频的大学生&#xff0c;找到合适的车在路上行驶的视频素材是非常重要的。不论你是制作城市宣传片、汽车广告&#xff0c;还是交通相关的教学视频&#xff0c;高质量的视频素材都能显著提升作品的专业性。今天&#xff0c;我为大家推荐几个优秀的网站&#xf…
阅读更多...
unity中预制体的移动-旋转-放缩

unity中预制体的移动-旋转-放缩

unity中预制体的移动-旋转-放缩 左上侧竖栏图标介绍Tools(手形工具)Move Tool(移动工具&#xff0c;单位米)Rotate Tool(旋转工具&#xff0c;单位角度)Scale Tool(缩放工具&#xff0c;单位倍数)Rect Tool(矩形工具)Transform Tool(变换工具)图标快捷键对照表工具使用的小技巧…
阅读更多...
用Pyhon写一款简单的益智类小游戏——2048

用Pyhon写一款简单的益智类小游戏——2048

文字版——代码及讲解 代码—— import random# 初始化游戏棋盘 def init_board():return [[0] * 4 for _ in range(4)]# 在棋盘上随机生成一个2或4 def add_new_tile(board):empty_cells [(i, j) for i in range(4) for j in range(4) if board[i][j] 0]if empty_cells:i,…
阅读更多...
【UBuntu20 配置usb网卡】 记录Ubuntu20配置usb网卡（特别是建立热点）

【UBuntu20 配置usb网卡】 记录Ubuntu20配置usb网卡（特别是建立热点）

【UBuntu20 配置usb网卡】 Ubuntu20配置usb网卡&#xff08;特别是建立热点&#xff09; 一、 闲言碎语的前言 usb的外置网卡&#xff0c;相比Windows即插即用&#xff0c;Linux买回来一顿折腾&#xff0c;准备把过程梳理一下记录起来。 网卡的方案其实就那几家&#xff0c;…
阅读更多...
Training-free layout control with cross-attention guidance

Training-free layout control with cross-attention guidance

https://zhuanlan.zhihu.com/p/666445024https://zhuanlan.zhihu.com/p/666445024 支持两种模式，1.sd文生图；2.绑定了dreambooth和text inversion的图像编辑。 # ------------------ example input ------------------examples &
阅读更多...
微信网页授权回调地址放多个参数的方法

微信网页授权回调地址放多个参数的方法

https://open.weixin.qq.com/connect/oauth2/authorize?appidAPPID&redirect_uriREDIRECT_URI&response_typecode&scopeSCOPE&stateSTATE#wechat_redirect 跳转后地址 redirect_uri/?codeCODE&stateSTATE。 redirect_uri如果不进行urlencode编码, 跳转后…
阅读更多...
Virtuoso使用layout绘制版图、使用Calibre验证DRC和LVS

Virtuoso使用layout绘制版图、使用Calibre验证DRC和LVS

1 绘制版图 1.1 进入Layout XL 绘制好Schmatic后&#xff0c;在原理图界面点击Launch&#xff0c;点击Layout XL进入版图绘制界面。 1.2 导入元件 1、在Layout XL界面左下角找到Generate All from Source。 2、在Generate Layout界面&#xff0c;选中“Instance”&#…
阅读更多...
「Mac畅玩鸿蒙与硬件13」鸿蒙UI组件篇3 - TextInput 组件获取用户输入

「Mac畅玩鸿蒙与硬件13」鸿蒙UI组件篇3 - TextInput 组件获取用户输入

在鸿蒙应用开发中，TextInput 组件用于接收用户输入，适用于文本、密码等多种输入类型。本文详细介绍鸿蒙 TextInput 组件的使用方法，包括输入限制、样式设置、事件监听及搜索框应用，帮助你灵活处理鸿蒙应用中的用户输入。 关键词 TextInput 组件用户输入输入限制事件监听搜索…
阅读更多...
偷懒总结篇|贪心算法|动态规划|单调栈|图论

偷懒总结篇|贪心算法|动态规划|单调栈|图论

由于这周来不及了&#xff0c;先过一遍后面的思路&#xff0c;具体实现等下周再开始详细写。 贪心算法 这个图非常好 122.买卖股票的最佳时机 II(妙&#xff0c;拆分利润) 把利润分解为每天为单位的维度&#xff0c;需要收集每天的正利润就可以&#xff0c;收集正利润的区间…
阅读更多...
时序数据分析：时序分割

时序数据分析：时序分割

目录 0 工况的定义 1 Changepoint 2 TreeSplit 3 Autoplait 4 应用示例 5.分析结论 0 工况的定义 工业设备系统在不同的外部条件&#xff08;即工况&#xff09;下&#xff0c;往往有多种运行模式&#xff0c;工业生产也往往会分阶段进行&#xff0c;在不同工况下&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023