激活函数(Activation Function) 是神经网络中的一个关键组件,负责将输入的线性组合转化为非线性输出。它赋予神经网络模型以复杂的表达能力,使其能够处理非线性问题,比如分类、图像识别和自然语言处理等任务。
1. 激活函数的作用
激活函数的主要作用是引入非线性,让神经网络能够学习复杂的模式。如果没有激活函数,神经网络中的每一层都只做线性变换,最终网络只会是多个线性变换的组合,相当于一个单一的线性模型,无法解决复杂的非线性问题。
- 非线性:激活函数将线性输出(加权和加偏置的输出)转化为非线性输出,使得神经网络可以拟合任意复杂的函数。
- 归一化:有些激活函数还具有将输出值限制在某个固定区间的效果(如 Sigmoid,将输出限制在 ( 0 , 1 ) (0, 1) (0,1) 区间),这可以帮助模型稳定训练。
2. 常见的激活函数
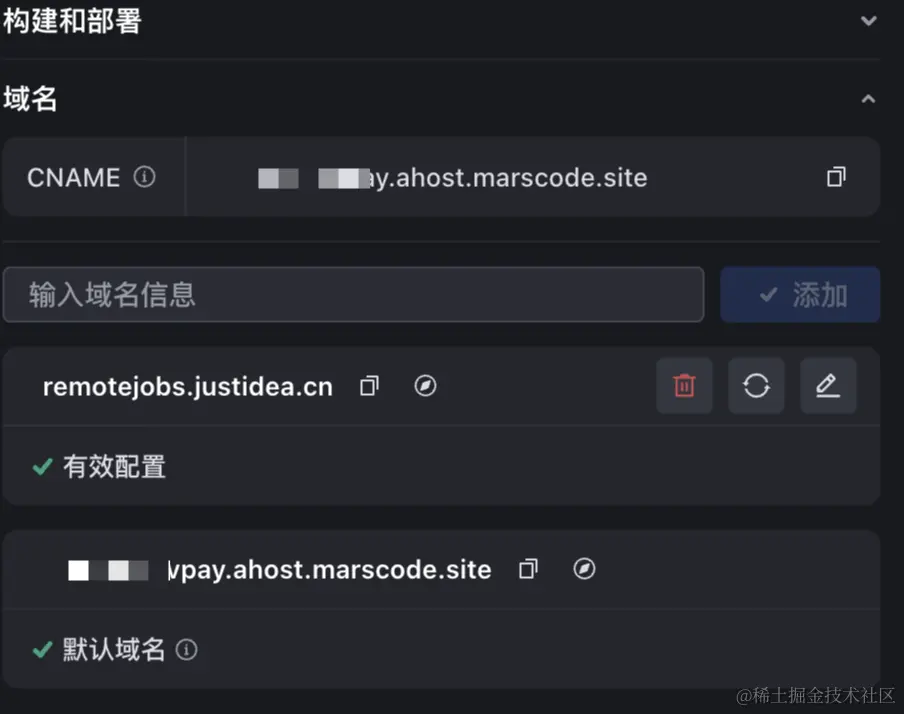
a. Sigmoid 函数
Sigmoid 函数是深度学习中最早广泛使用的激活函数之一,它将输入值映射到
(
0
,
1
)
(0, 1)
(0,1) 的区间,输出为一个概率值。其公式为:
σ
(
x
)
=
1
1
+
e
−
x
\sigma(x) = \frac{1}{1 + e^{-x}}
σ(x)=1+e−x1
-
特点:输出值在 0 0 0 到 1 1 1 之间,因此常用于二分类问题。
-
缺点:梯度消失问题,在输入值较大或较小时,Sigmoid 函数的梯度(导数)接近零,这会导致反向传播过程中梯度逐渐减小(消失),影响权重的更新,特别是在深层网络中。
-
图示:

b. Tanh 函数
Tanh(双曲正切函数)是 Sigmoid 的扩展版本,输出范围为
(
−
1
,
1
)
(-1, 1)
(−1,1),可以解决 Sigmoid 在输出上的偏移问题。其公式为:
tanh
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
\text{tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
tanh(x)=ex+e−xex−e−x
-
特点:输出范围为 ( − 1 , 1 ) (-1, 1) (−1,1),相比 Sigmoid 更加居中,能够减少偏移(mean shift)问题。
-
缺点:同样存在梯度消失问题,在输入值非常大或非常小时,Tanh 的梯度依然会变得很小。
-
图示:

c. ReLU(Rectified Linear Unit)函数
ReLU 是目前使用最为广泛的激活函数之一。ReLU 函数的输出在正数区域保持线性,在负数区域则为 0。其公式为:
ReLU
(
x
)
=
max
(
0
,
x
)
\text{ReLU}(x) = \max(0, x)
ReLU(x)=max(0,x)
-
特点:当输入大于 0 时,ReLU 直接输出输入值;当输入小于 0 时,输出为 0。
-
优点:
- 解决梯度消失问题:ReLU 的梯度为 1(当 x > 0 x > 0 x>0 时),不会像 Sigmoid 和 Tanh 那样使梯度变小,从而有效缓解梯度消失问题。
- 计算效率高:ReLU 计算非常简单,只需要一个最大值操作,非常适合在深层网络中使用。
-
缺点:死亡 ReLU 问题,当输入的值小于 0 时,ReLU 的输出一直为 0,这意味着神经元可能会永远不再激活,这在某些情况下会导致网络性能下降。
-
图示:

d. Leaky ReLU
Leaky ReLU 是对 ReLU 的一种改进,解决了 ReLU 在负数区域输出为 0 时神经元“死亡”的问题。Leaky ReLU 在负数区域给予一个很小的正数斜率
α
\alpha
α(通常为 0.01)而不是完全为 0,其公式为:
Leaky ReLU
(
x
)
=
{
x
if
x
>
0
α
x
if
x
≤
0
\text{Leaky ReLU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases}
Leaky ReLU(x)={xαxif x>0if x≤0
-
优点:在负数区域仍然保持一个小的斜率,使得神经元不完全失活。减少了 ReLU 函数中的死亡 ReLU 问题,确保神经元即使在负值输入时也能有一定的梯度更新。
-
图示:

e. ELU(Exponential Linear Unit)
ELU 是另一种改进的 ReLU 激活函数,在负数区域使用指数函数进行平滑。其公式为:
ELU
(
x
)
=
{
x
if
x
>
0
α
(
e
x
−
1
)
if
x
≤
0
\text{ELU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha(e^x - 1) & \text{if } x \leq 0 \end{cases}
ELU(x)={xα(ex−1)if x>0if x≤0
其中
α
\alpha
α 是一个超参数,通常取值为 1。
-
特点:在正数区域与 ReLU 类似,但在负数区域使用指数函数进行平滑,避免了死亡 ReLU 问题。
-
优点:与 Leaky ReLU 相比,ELU 在负数区域提供的平滑曲线可以在一定程度上减少偏差。
-
缺点:计算量比 ReLU 稍大,因为负数区域的计算涉及指数运算。
-
图示:

f. Swish
Swish 是一种新的激活函数,由 Google 提出,它结合了 ReLU 和 Sigmoid 的优势。其公式为:
Swish
(
x
)
=
x
⋅
σ
(
x
)
=
x
⋅
1
1
+
e
−
x
\text{Swish}(x) = x \cdot \sigma(x) = x \cdot \frac{1}{1 + e^{-x}}
Swish(x)=x⋅σ(x)=x⋅1+e−x1
-
特点:Swish 在小于 0 的输入值时逐渐趋近于 0,而在大于 0 时逐渐增大,因此它在负值区域不会像 ReLU 那样硬性截断。
-
优点:Swish 的非线性变化更加平滑,能够捕获更多的复杂模式,特别适合用于深度神经网络中。
-
缺点:计算量比 ReLU 更大,因为它涉及 Sigmoid 的计算。
-
图示:

3. 激活函数的选择
神经网络中的激活函数选择取决于具体任务和网络结构。以下是一些常见的经验法则:
-
ReLU 是目前最常用的激活函数,特别是在卷积神经网络(CNN)和全连接网络(FCN)中表现优异。对于大多数深度网络,ReLU 是一个很好的起点,因为它能有效避免梯度消失问题。
-
Leaky ReLU 和 ELU 是 ReLU 的改进版本,适合于有负输入的场景或避免神经元失活的场景。
-
Sigmoid 和 Tanh 适用于一些特殊情况,特别是在需要输出概率或对称输出的情况下(例如,输出为 [ − 1 , 1 ] [-1, 1] [−1,1])。不过它们通常会导致梯度消失,因此不推荐用于深层网络。
-
Swish 是一种更平滑的激活函数,在某些复杂任务(如超深网络)上可能表现优异。
4. 激活函数的数学属性
激活函数的选择不仅仅与模型的表现有关,还涉及其数学属性,如:
-
可微性:大多数常见的激活函数(如 Sigmoid、Tanh、ReLU 等)都是可微的,尽管 ReLU 在 x = 0 x=0 x=0 处不可微,但通常在实际应用中表现良好。
-
导数值的大小:激活函数的导数决定了梯度传播时的效率。像 ReLU 这样导数为常数的函数不会引发梯度消失,而 Sigmoid 和 Tanh 由于导数较小,容易引发梯度消失问题。