512.找树左下角的值
给定一个二叉树,在树的最后一行找到最左边的值。
示例 1:

示例 2:

思路:
递归三部曲:
- 参数和返回值:传入节点是参数,返回值是最终值int
- 终止条件:遇到空节点直接返回,或者遇到叶子节点(没有孩子)的时候,判断此时的深度和已记录的最大深度进行比较,如果此时更大就更新结果值,然后返回。遇到同层的其他节点,由于深度相同,并不会覆盖这个值。
- 递归逻辑:当此节点不是叶子节点时,如果左孩子存在先对左孩子调用递归,然后再判断右孩子是否存在,调用递归。
代码实现如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
if not root:
return None
self.maxdepth = 0
self.result = root.val
self.findleftleaf(root, 1)
return self.result
def findleftleaf(self, node:Optional[TreeNode], depth:int):
if not node:
return
if not node.left and not node.right:
if depth > self.maxdepth:
self.maxdepth = depth
self.result = node.val
return
if node.left:
self.findleftleaf(node.left, depth+1)
if node.right:
self.findleftleaf(node.right, depth+1)
return迭代:当然,还可以使用我们最喜欢的层序遍历,一样记录最大深度,同个深度只比较第一个遇到的节点,同层的其他节点不需要比较,这里不另外实现了,直接附上参考代码:
# Definition for a binary tree node.# class TreeNode:# def __init__(self, val=0, left=None, right=None):# self.val = val# self.left = left# self.right = rightfrom collections import dequeclass Solution:
def findBottomLeftValue(self, root):
if root is None:
return 0
queue = deque()
queue.append(root)
result = 0
while queue:
size = len(queue)
for i in range(size):
node = queue.popleft()
if i == 0:
result = node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result
112. 路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22,
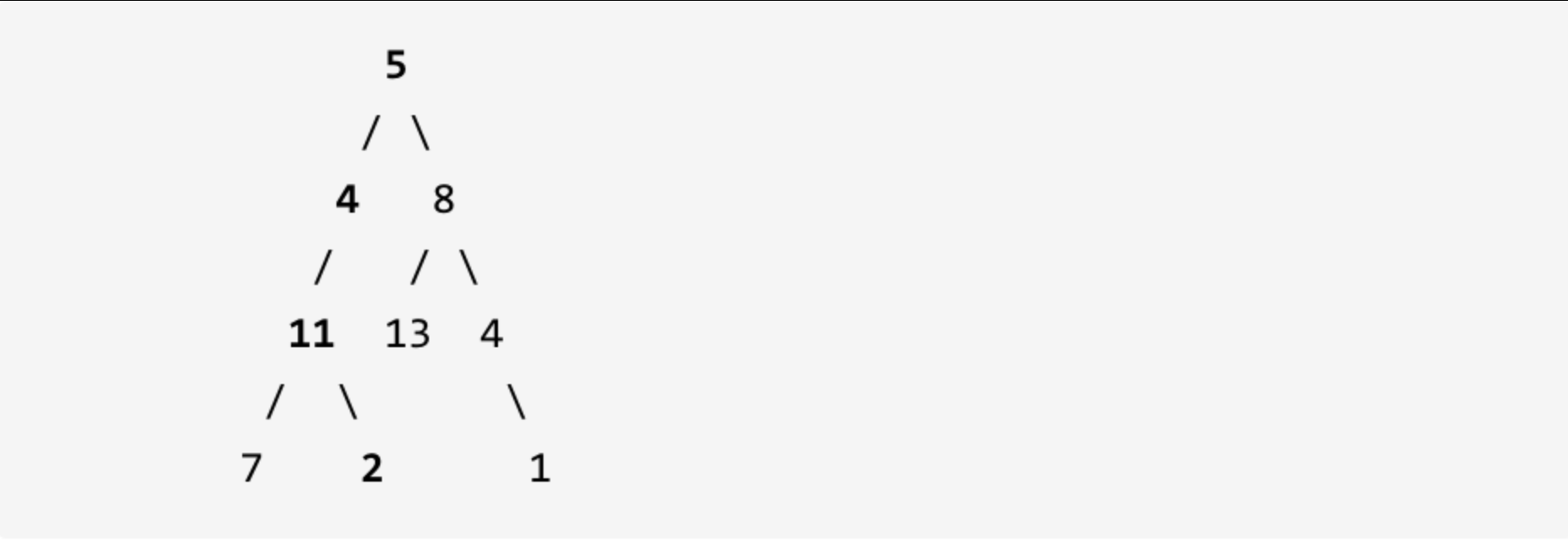
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
思路:
递归三部曲:
- 参数和返回值:参数是传入节点,和记录当前路径总和的值。返回值是bool
- 终止条件:当节点为空返回False。当节点没有孩子(是叶子节点),判断此时是否满足条件,满足条件返回True,否则返回False。
- 递归逻辑:如果当前节点不是叶子节点,将当前值加入当前路径总和的值,然后传入他的孩子的递归函数参数中,进行递归调用。如果得到一个True,直接返回True。
代码实现如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
self.target = targetSum
return self.getpath(root, 0)
def getpath(self, node: Optional[TreeNode], cur: int) -> bool:
if not node:
return False
if not node.left and not node.right:
if (cursum := cur + node.val) != self.target:
return False
else:
return True
if node.left:
if self.getpath(node.left, cur+node.val):
return True
if node.right:
if self.getpath(node.right, cur+node.val):
return True
return False规范代码如下:
# Definition for a binary tree node.# class TreeNode:# def __init__(self, val=0, left=None, right=None):# self.val = val# self.left = left# self.right = rightclass Solution:
def traversal(self, cur: TreeNode, count: int) -> bool:
if not cur.left and not cur.right and count == 0: # 遇到叶子节点,并且计数为0
return True
if not cur.left and not cur.right: # 遇到叶子节点直接返回
return False
if cur.left: # 左
count -= cur.left.val
if self.traversal(cur.left, count): # 递归,处理节点
return True
count += cur.left.val # 回溯,撤销处理结果
if cur.right: # 右
count -= cur.right.val
if self.traversal(cur.right, count): # 递归,处理节点
return True
count += cur.right.val # 回溯,撤销处理结果
return False
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if root is None:
return False
return self.traversal(root, sum - root.val) 113. 路径总和ii
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22,
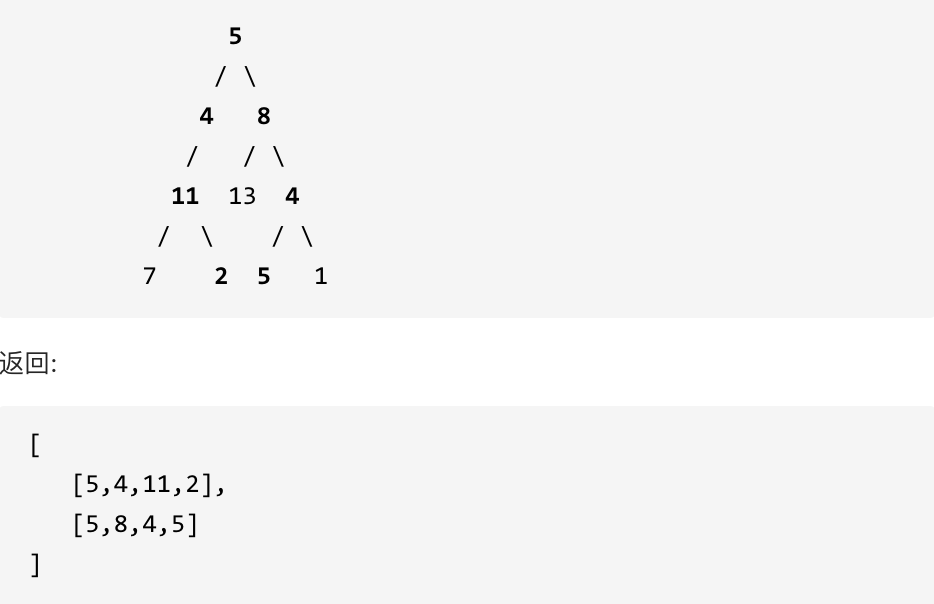
思路:与上一题的区别仅在于,要记录所有的路径,遇到一个符合条件的也不停止递归。
省略分析,代码实现如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
if not root:
return []
self.result = []
self.target = targetSum
self.getpath(root, 0, [])
return self.result
def getpath(self, node: Optional[TreeNode], cur:int, path: List) -> None:
path.append(node.val)
if not node.left and not node.right:
if (cursum := cur + node.val) == self.target:
self.result.append(path)
return
else:
return
if node.left:
self.getpath(node.left, cur+node.val, path[:])
if node.right:
self.getpath(node.right, cur+node.val, path[:])
return规范代码:
# Definition for a binary tree node.# class TreeNode:# def __init__(self, val=0, left=None, right=None):# self.val = val# self.left = left# self.right = rightclass Solution:
def __init__(self):
self.result = []
self.path = []
def traversal(self, cur, count):
if not cur.left and not cur.right and count == 0: # 遇到了叶子节点且找到了和为sum的路径
self.result.append(self.path[:])
return
if not cur.left and not cur.right: # 遇到叶子节点而没有找到合适的边,直接返回
return
if cur.left: # 左 (空节点不遍历)
self.path.append(cur.left.val)
count -= cur.left.val
self.traversal(cur.left, count) # 递归
count += cur.left.val # 回溯
self.path.pop() # 回溯
if cur.right: # 右 (空节点不遍历)
self.path.append(cur.right.val)
count -= cur.right.val
self.traversal(cur.right, count) # 递归
count += cur.right.val # 回溯
self.path.pop() # 回溯
return
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
self.result.clear()
self.path.clear()
if not root:
return self.result
self.path.append(root.val) # 把根节点放进路径
self.traversal(root, sum - root.val)
return self.result迭代:
# Definition for a binary tree node.# class TreeNode:# def __init__(self, val=0, left=None, right=None):# self.val = val# self.left = left# self.right = rightclass Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:
if not root:
return []
stack = [(root, [root.val])]
res = []
while stack:
node, path = stack.pop()
if not node.left and not node.right and sum(path) == targetSum:
res.append(path)
if node.right:
stack.append((node.right, path + [node.right.val]))
if node.left:
stack.append((node.left, path + [node.left.val]))
return res106.从中序与后序遍历序列构造二叉树
根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
- 中序遍历 inorder = [9,3,15,20,7]
- 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树:

此篇以记录为主,自己基本没啥思路,实现的代码能看懂但过程的具体过程还是掌握不到位,二刷复习的时候好好掌握。
代码随想录
第一步:如果数组大小为零的话,说明是空节点了。
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
第五步:切割后序数组,切成后序左数组和后序右数组
第六步:递归处理左区间和右区间
此时应该注意确定切割的标准,是左闭右开,还有左开右闭,还是左闭右闭,这个就是不变量,要在递归中保持这个不变量。
在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭右闭,必然乱套!
首先要切割中序数组,为什么先切割中序数组呢?
切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必要先切割中序数组。
中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割
接下来就要切割后序数组了。
首先后序数组的最后一个元素指定不能要了,这是切割点 也是 当前二叉树中间节点的元素,已经用了。
后序数组的切割点怎么找?
后序数组没有明确的切割元素来进行左右切割,不像中序数组有明确的切割点,切割点左右分开就可以了。
此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。
中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
106. 从前序与中序遍历序列构造二叉树:
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
if not preorder:
return None
# 第二步: 前序遍历的第一个就是当前的中间节点.
root_val = preorder[0]
root = TreeNode(root_val)
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割preorder数组. 得到preorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟前序数组大小是相同的.
preorder_left = preorder[1:1 + len(inorder_left)]
preorder_right = preorder[1 + len(inorder_left):]
# 第六步: 递归
root.left = self.buildTree(preorder_left, inorder_left)
root.right = self.buildTree(preorder_right, inorder_right)
# 第七步: 返回答案
return root105.从中序与后序遍历序列构造二叉树:
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. (递归终止条件)
if not postorder:
return None
# 第二步: 后序遍历的最后一个就是当前的中间节点.
root_val = postorder[-1]
root = TreeNode(root_val)
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割postorder数组. 得到postorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
postorder_left = postorder[:len(inorder_left)]
postorder_right = postorder[len(inorder_left): len(postorder) - 1]
# 第六步: 递归
root.left = self.buildTree(inorder_left, postorder_left)
root.right = self.buildTree(inorder_right, postorder_right)
# 第七步: 返回答案
return root