目录

约瑟夫环plus

孩子们的游戏​编辑

解法二.动态规划

大数加法

牛客.在字符串中找出连续的最长数字串

力扣703.数据流中第K大元素​编辑

---

约瑟夫环plus

孩子们的游戏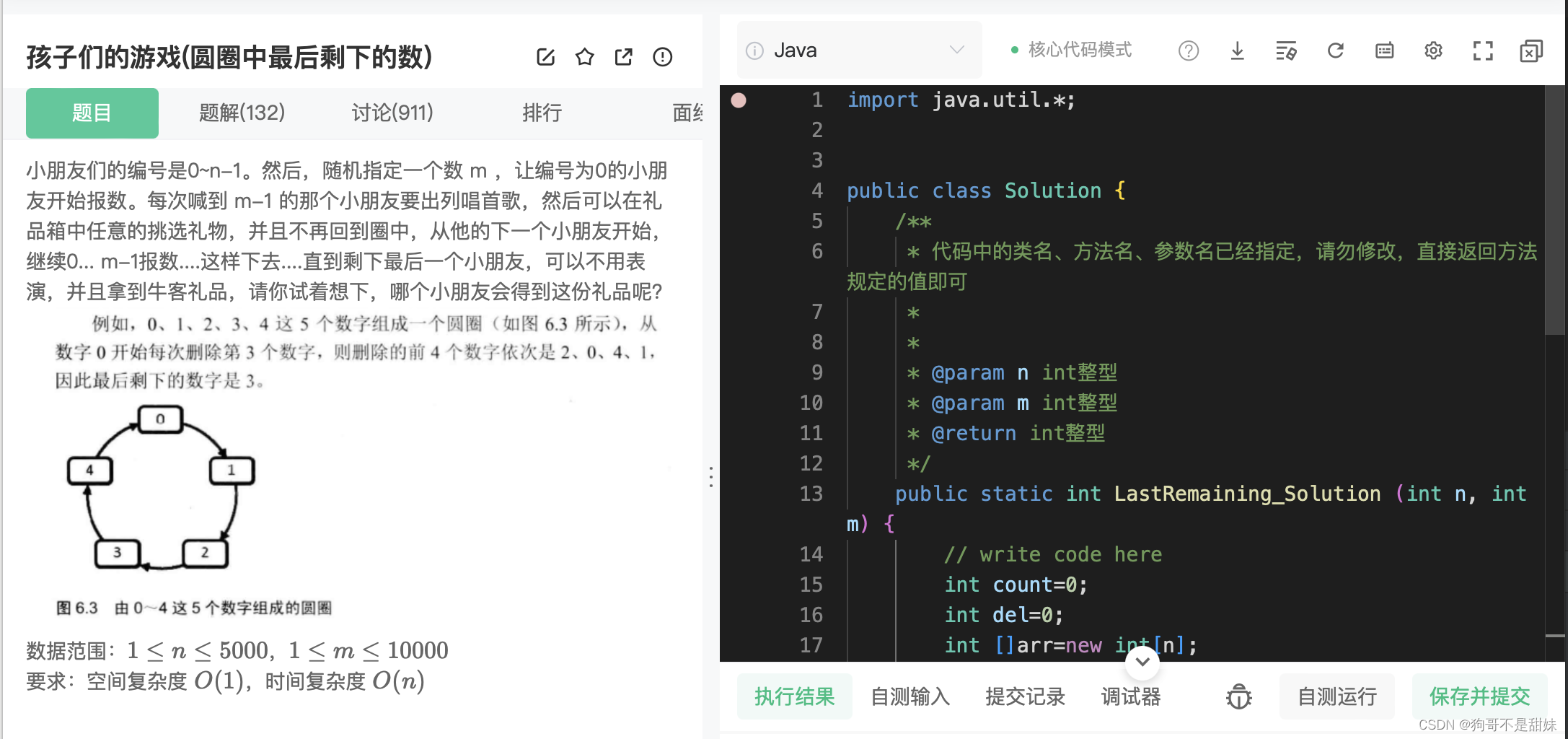

基本模拟，没啥特殊技巧

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param n int整型
     * @param m int整型
     * @return int整型
     */
    public static int LastRemaining_Solution (int n, int m) {
        // write code here
        int count=0;
        int del=0;
        int []arr=new int[n];
        for(int i=0;i<n;i++){
            arr[i]=i;}
        while(del!=n-1){
            for(int i=0;i<n;i++){
                if(count==m-1&&arr[i]>-1){
                    arr[i]=-1;
                    count=0;
                    del++;
                }
                if(arr[i]>-1){
                    count++;
                }
                if(del==n-1){
                    break;
                }
            }
        }
        for(int i=0;i<n;i++){
            if(arr[i]!=-1){
                return arr[i];
            }
        }
        return 0;
    }
}

解法二.动态规划

1.状态表示:

dp[i]:当有i个孩子围成一圈时候最终获胜的孩子的编号

dp[1]=0 

状态转移方程:那么我们选择从里面的圈开始推，dp[n]=dp[n-1]+m

就是在里面n-1个人都已经获胜了，那么最外面的n个人获胜的也是它，那么我们只需要知道里面圆圈怎么推外面的关系。+m就会变成外面的坐标，当然他有可能加的很大，此时需要%n

​​​​​​​

大数加法

import java.util.*;

import java.math.BigInteger;
public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 计算两个数之和
     * @param s string字符串 表示第一个整数
     * @param t string字符串 表示第二个整数
     * @return string字符串
     */

    public static String solve (String s, String t) {
        // write code here、
        BigInteger bigInteger1 = new BigInteger(s);
        BigInteger bigInteger2 = new BigInteger(t);
        ;
        return String.valueOf(bigInteger1.add(bigInteger2));
    }
}

牛客.在字符串中找出连续的最长数字串

思路，使用应该是双指针，在加上转变成字符数组，再去用ac码来做，因为大A65,小a97，我们只需要0-9即可。

力扣703.数据流中第K大元素

题意不好理解:但是代码很好写（蛮简单的还是），前k个大的，就去建立小堆，然后和堆顶比，假如比堆顶大，就入堆，然后pop,比堆顶小，出去

class KthLargest {
   PriorityQueue<Integer>heap;
   int _k;
    public KthLargest(int k, int[] nums) {
    _k=k;
    heap=new PriorityQueue<>();
    for(int i=0;i<nums.length;i++{
        heap.offer(nums[i]);
        if(heap.size()>_k){
            heap.poll();
        }
    }
}
    
    public int add(int val) {
     heap.offer(val);
     if(heap.size()>_k){
        heap.poll();
     }
     return heap.peek();
    }
}

/**
 * Your KthLargest object will be instantiated and called as such:
 * KthLargest obj = new KthLargest(k, nums);
 * int param_1 = obj.add(val);
 */