目录
概述
核心概念:堆
堆结构
数组存堆
思路
算法过程
up()
down()
Code
优化方案
大根堆优化
Code(pro)
复杂度
总结
概述
在「数组」快速排序 / 随机值优化|小区间插入优化(C++)中,我们介绍了三种基本排序中的冒泡排序与分治思想结合的算法:快速排序。
本文我们来讲第二种基本排序:选择排序与分治思想结合的产物:堆排序。
我们来回想选择排序:每次选出最小的元素放在数组头部位置,每次都扫描一遍整个数组,整体表现为O(n²)。
我们希望只进行少量比较就能得出数组中的最小元素,该怎么做呢?堆这种结构给了我们一点启发。
核心概念:堆
堆是一颗完全二叉树,它的特点是可以用一维数组来储存。
堆结构
在初学数组排序阶段就理解二叉树似乎有些困难,不过好在我们不必完全了解二叉树的所有概念。
我们只需要知道:
①一个堆是一个层状结构,除去最底一层,每层的每个节点都有左子节点和右子节点,层层布满。
节点从上到下,从左到右依次编号。
(对于这样的结构,我们称之为二叉树,每个父节点都有左右孩子指针指向子节点。)

②只有最后一层允许节点不排满,但节点的排布仍然是严格从左到右的。
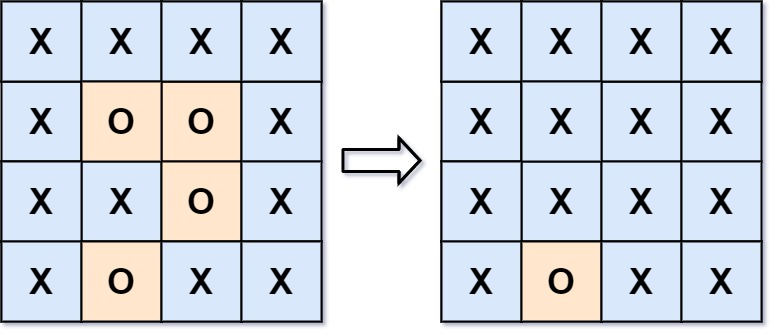
如下,图一和图二都是堆,但图三不是堆,因为它的最底层排布不是从左到右的。



③堆有两种:小根堆和大根堆。
小根堆要求父节点的值小于它的两个孩子,大根堆要求父节点的值大于它的两个孩子。
我们称二叉树的头结点为根,所以这种命名就很好理解了:小根堆的根最小,大根堆的根最大。
数组存堆
此时此刻我们完全不必知道二叉树的标准结构,因为数组就可以储存堆。
观察:

我们发现,一个序号从0开始的堆结构,
对于第idx个节点:
父节点序号:(idx-1)/2。
左子节点序号:idx*2+1。
右子节点序号:idx*2+2。
也就是说,对于上图这样的堆,我们将它存入数组应该是这样的:
i 0 1 2 3 4 5 6
int arr[i] 10 15 30 40 50 100 40因此,对于一个堆,我们可以用数组来表示它。
思路
堆这种结构只是为我们的选择排序优化服务的。
选择排序需要我们每次找到最小的元素,那么我们不妨对数组建堆(又称堆化),获得一个小根堆数组后,堆顶,也就是序号为0的数组位置,自然就是我们要的最小元素。
获得最小元素后堆顶出堆,对剩余元素重新堆化,堆顶每次都是剩余元素中的最小元素。
我们不断进行堆顶出堆,就实现了选择排序。
考虑到堆化是按层实现的,因此若有n个元素,则有logn层,重新堆化的过程中内部重排最多进行logn次,通过logn次比较获得最小元素,这显然优于暴力选择排序。
算法过程
堆排序由两个操作构成:上浮up和下沉down。
我们先用宏定义描述一下节点父子关系,另有swap函数实现功能封装:
#define father(x) ((x-1)/2)
#define lchild(x) (2*x+1)
#define rchild(x) (2*x+2)
void swap(int& a, int& b) {
int temp = b;
b = a, a = temp;
}up()
对数组进行初始堆化时,依靠上浮实现。
将堆的大小称为size,数组的整体长度称为len。
我们将数组arr分割成两部分:已经堆化的[0,size),未堆化的剩余部分[size,len)
我们将剩余部分的第一个数加入堆中,它显然处于堆底,为了让它处于小根堆中合适的位置,我们进行对它上浮操作。
int size = 0;
for (int i = 0; i < len; i++) {
up(arr, i);
size++;
}当idx为0时,不再上浮,否则判断此节点与其父亲的大小关系。
我们维护小根堆,所以如果父节点较大,则两者进行交换,使得父节点较小。
然后跟踪父节点,对父节点继续执行上浮操作。(这里的递归操作顺理成章的出现了)
void up(int arr[], int idx) {
if (idx && arr[father(idx)] > arr[idx]) {
swap(arr[father(idx)], arr[idx]);
up(arr, father(idx));
}
}down()
数组完全堆化后,我们开始进行堆顶出堆,实现选择排序。
我们使用小根堆,因此需要一个额外的辅助空间来承载结果(后续它会被我们的优化方案优化掉)。
堆顶出堆后将堆中的最后一个元素赋给堆顶,堆size缩小,然后开始对堆顶执行下沉操作。
int* assist = new int[len];
for (int j = 0; j < len; j++) {
assist[j] = arr[0];
arr[0] = arr[--size];
down(arr,0,size);
}
memcpy(arr, assist, sizeof(int) * len);
delete[] assist;定义pos,
①如果idx节点的左右孩子没有超出数组堆化范围,则pos等于左右孩子中较小的元素的索引,这是为了使得较小的元素总是位于堆的上部。
②如果idx的右孩子超出堆化范围,那么堆中只有左孩子是有效的,pos等于左孩子。
③如果idx的左孩子也超出堆化范围,说明idx已经在堆中沉底,没有后续元素,不必比较直接返回。
当pos位的元素小于idx位的元素时,两者作交换(即idx较大时,与其最小的子节点交换),然后跟踪pos,继续下沉。
void down(int arr[], int idx, int size) {
int pos;
if (rchild(idx) < size)pos = arr[lchild(idx)] < arr[rchild(idx)] ? lchild(idx) : rchild(idx);
else if (lchild(idx) < size)pos = lchild(idx);
else return;
if (arr[idx] > arr[pos]) {
swap(arr[idx], arr[pos]);
down(arr,pos,size);
}
}Code
#define father(x) ((x-1)/2)
#define lchild(x) (2*x+1)
#define rchild(x) (2*x+2)
void up(int arr[], int idx) {
if (idx && arr[father(idx)] > arr[idx]) {
swap(arr[father(idx)], arr[idx]);
up(arr, father(idx));
}
}
void down(int arr[], int idx, int size) {
int pos;
if (rchild(idx) < size)pos = arr[lchild(idx)] < arr[rchild(idx)] ? lchild(idx) : rchild(idx);
else if (lchild(idx) < size)pos = lchild(idx);
else return;
if (arr[idx] > arr[pos]) {
swap(arr[idx], arr[pos]);
down(arr,pos,size);
}
}
void heap_sort(int arr[], int len) {
int size = 0;
for (int i = 0; i < len; i++) {
size++;
up(arr, i);
}
int* assist = new int[len];
for (int j = 0; j < len; j++) {
assist[j] = arr[0];
arr[0] = arr[--size];
down(arr,0,size);
}
memcpy(arr, assist, sizeof(int) * len);
delete[] assist;
}优化方案
辅助数组assist看起来很愚蠢,我们来像个办法处理掉它。
大根堆优化
我们何不使用大跟堆来依次弹出数组的最大元素呢?
小根堆是从前往后进行最小值选择排序,因此无法安放在原始数组中(因为堆化部分会占据数组的前面部分),但大根堆解决了这个问题。
考虑到弹出时堆size收缩,因此数组的末尾会空出一个位置,我们可以直接将弹出元素安放到该位置上。
Code(pro)
#define father(x) ((x-1)/2)
#define lchild(x) (2*x+1)
#define rchild(x) (2*x+2)
void bigger_up(int arr[], int idx) {
if (idx && arr[father(idx)] < arr[idx]) {
swap(arr[father(idx)], arr[idx]);
bigger_up(arr, father(idx));
}
}
void smaller_down(int arr[], int idx, int size) {
int pos;
if (rchild(idx) < size)pos = arr[lchild(idx)] > arr[rchild(idx)] ? lchild(idx) : rchild(idx);
else if (lchild(idx) < size)pos = lchild(idx);
else return;
if (arr[idx] < arr[pos]) {
swap(arr[idx], arr[pos]);
smaller_down(arr, pos, size);
}
}
void HPsort(int arr[], int len) {
int size = 0;
for (int i = 0; i < len; i++,size++)
bigger_up(arr, i);
while (size--) {
swap(arr[0], arr[size]);
smaller_down(arr, 0, size);
}
}*注意*:大根堆上浮大元素,沉底小元素。
复杂度
时间复杂度:O(nlogn)
空间复杂度:O(logn)
复杂度分析:
时间分析:{
考虑堆化是按层实现的,因此若有n个元素,则有logn层。
对n个元素建堆,每个元素按层上浮,最多比较logn次,得到O(nlogn)
对n个元素出堆,弹出堆顶后将堆尾赋给堆顶,每个元素按层下沉,最多比较logn次,得到O(nlogn)
O(nlogn)+O(nlogn)=O(2nlogn)=O(nlogn)。
}
空间分析:{
使用大跟堆建堆时,不使用额外空间承载答案。
建堆和出堆时调用递归函数进行压栈,函数最多调用logn层,最多占据空间O(logn)。
}
总结
堆为我们提供了一种新的视角来处理数组的最小元素,它的另一个重大用途就是实现优先队列priority_queue。
堆排序的分治策略也比较新颖:他不是在算法思想上进行分治,而是利用模拟堆这种数据结构进行分治,希望可以为你带来对分治思想的新启发。