---

• 原题链接：62. 不同路径

---

1- 思路

题目识别

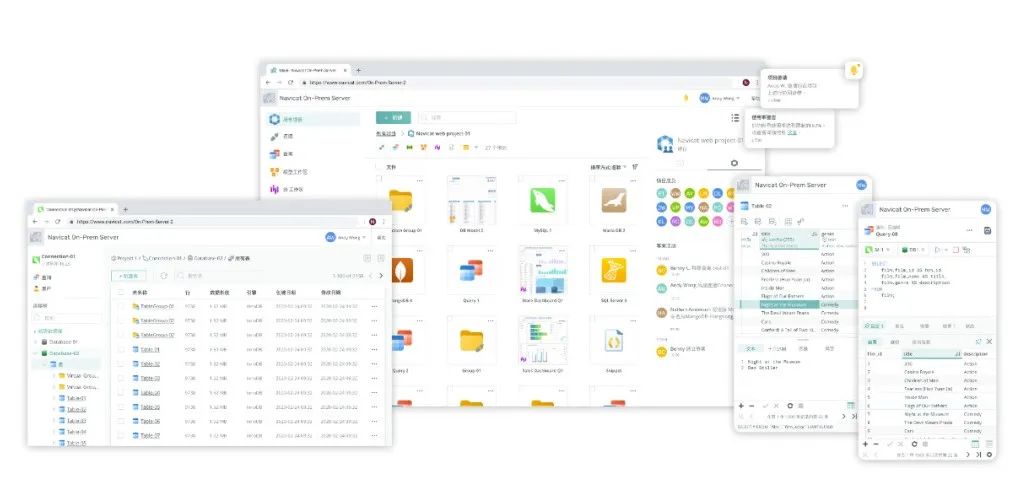
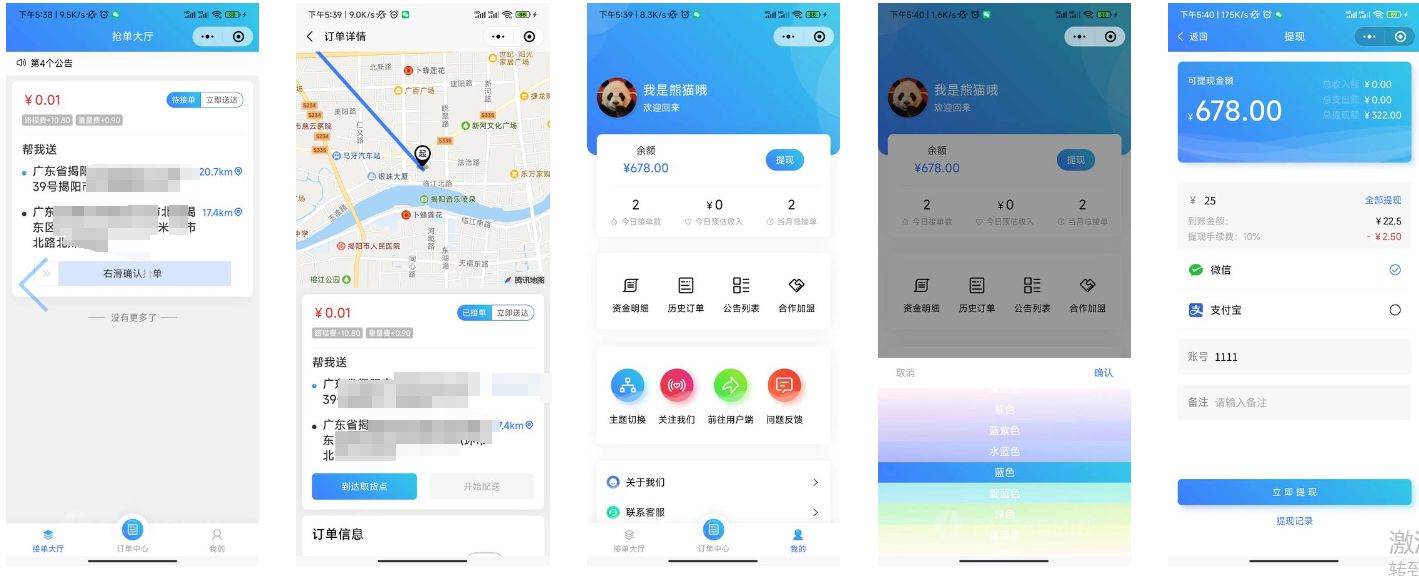
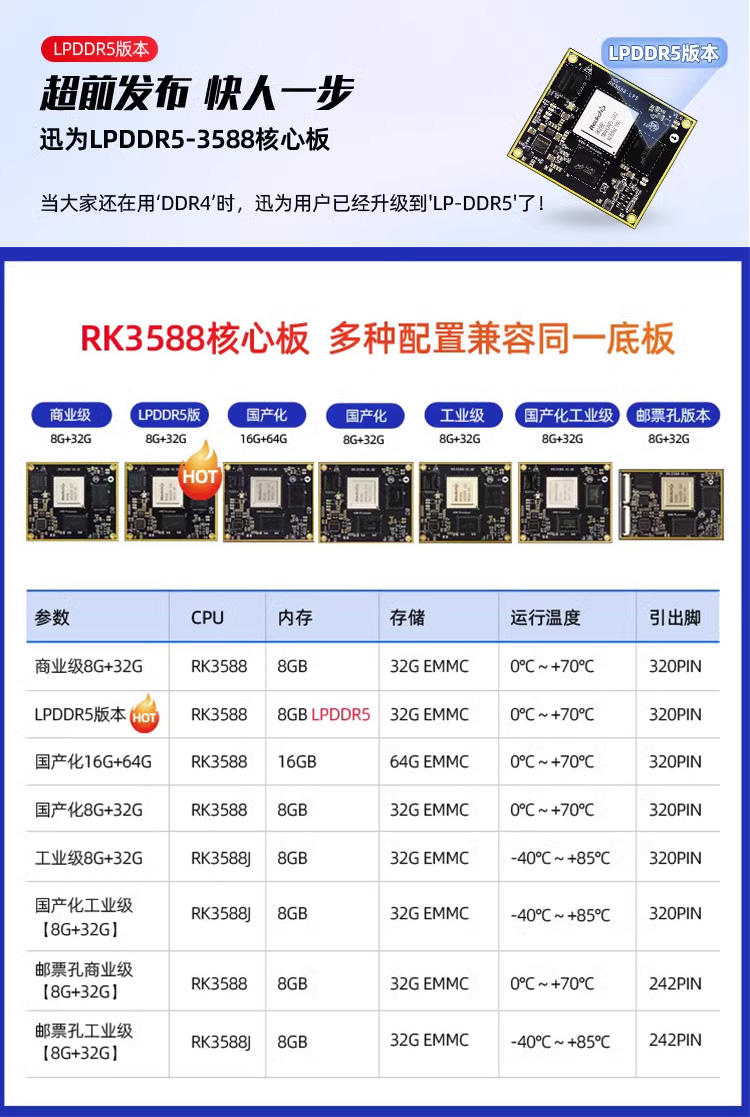
• 识别1 ：给一个二维矩阵，每次只能向下或者向右移动一步
• 识别2：求解到达最右下角的路径数。

动规五部曲

• 1- 定义 dp 数组，确定含义
  • dp[i][j] 代表到达单元格 [i][j] 的路径数
• 2- 递推公式
  • 因为只能向下或者向右移动，因此当前位置的方式由两个方向推导而来
  • dp[i][j] = dp[i-1][j] + dp[i][j-1]
• 3- 初始化
  • 第一行，第一列的方式都是 1
• 4- 遍历顺序，二维遍历 分别都从 1 开始

---

2- 实现

⭐62. 不同路径——题解思路

class Solution {
    public int uniquePaths(int m, int n) {
        // 1. 定义 dp
        int[][] dp = new int[m][n];

        // 2. 递推
        // dp[i][j] = dp[i-1][j] + dp[i][j-1]

        // 3. 初始化
        for(int i = 0 ; i < m ; i++){
            dp[i][0] = 1;
        }
        for(int i = 0 ; i < n;i++){
            dp[0][i] = 1;
        }

        // 4.遍历顺序
        for(int i = 1 ; i < m ; i++){
            for(int j = 1 ; j < n ; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

---

3- ACM 实现

public class uniquePaths {

    public static int uniquePaths(int m, int n) {
        // 1. 定义 dp
        int[][] dp = new int[m][n];

        // 2. 递推
        // dp[i][j] = dp[i-1][j] + dp[i][j-1]

        // 3. 初始化
        for(int i = 0 ; i < m ; i++){
            dp[i][0] = 1;
        }
        for(int i = 0 ; i < n;i++){
            dp[0][i] = 1;
        }

        // 4.遍历顺序
        for(int i = 1 ; i < m ; i++){
            for(int j = 1 ; j < n ; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }


    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = sc.nextInt();
        System.out.println("结果是"+uniquePaths(m,n));
    }
}