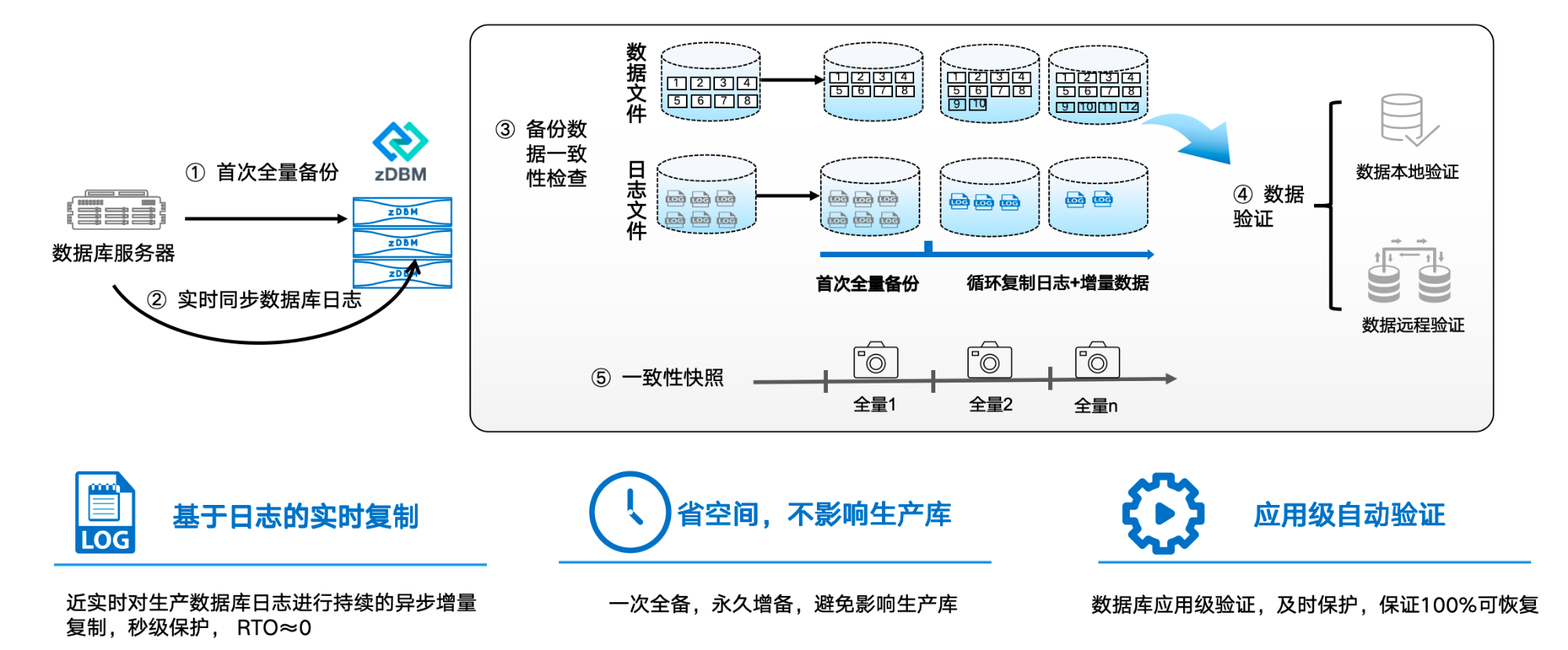
1. 概念

在一个有向无环图(DAG)中，根据节点的依赖关系，对所有的节点进行线性排序的算法

拓扑排序的结果不一定是唯一的

2. 实现

2.1 BFS（卡恩算法）

1、步骤

2、代码实现

以KamaCoder 117.软体构建
题目：117. 软件构建 (kamacoder.com)

class Program
{
    public static void Main(string[] args)
    {
        // 处理输入
        string[] dimensions = Console.ReadLine().Split();
        int n = int.Parse(dimensions[0]);
        int m = int.Parse(dimensions[1]);
        // 邻接表 && 入度
        List<int>[] graph = new List<int>[n];
        for (int i = 0; i < n; i++)
        {
            graph[i] = new List<int>();
        }
        int[] indegree = new int[n];
        for (int i = 0; i < m; i++)
        {
            string[] nodes = Console.ReadLine().Split();
            int parent = int.Parse(nodes[0]);
            int child = int.Parse(nodes[1]);
            graph[parent].Add(child);
            indegree[child]++;
        }


        // TS & 输出
        List<int> result = new List<int>();
        TStra(graph, indegree, result, n);
        Console.WriteLine(result.Count == n ? string.Join(" ", result) : "-1");
    }

    public static void TStra(List<int>[] graph, int[] indegree, List<int> result, int n)
    {
        Queue<int> nodes = new Queue<int>();
        for (int i = 0; i < indegree.Length; i++)
        {
            if (indegree[i] == 0)
            {
                nodes.Enqueue(i);
                indegree[i] = -1;
            }
        }
        if (nodes.Count == 0) return;

        while (nodes.Count > 0)
        {
            int cur = nodes.Dequeue();
            result.Add(cur);

            foreach (int child in graph[cur])
            {
                indegree[child]--;
            }
        }

        if (result.Count == n) return;
        else
        {
            TStra(graph, indegree, result, n);
        }
    }
}

2.2 DFS（待更）