论文阅读：MonoScene: Monocular 3D Semantic Scene Completion

Abstract

MonoScene提出了一个3D语义场景完成（SSC）框架，其中场景的密集几何形状和语义是从单个单目 RGB 图像中推断出来的。与SC文献不同，我们依靠2.5或3D输入，解决了2D到3D场景重建的复杂问题，同时联合推断其语义。我们的框架依赖于连续的2D和3D UNets，通过受光学启发的新型2D 3D特征投影来连接，并在强制执行空间语义一致性之前引入3D上下文关系。除了建筑贡献之外，我们还介绍了新颖的全局场景和local frustums 损失。实验表明，我们在所有指标和数据集上的表现都优于文献，同时甚至在相机视野之外也会产生看似合理的场景。我们的代码和经过训练的模型可在https://github.com/cv-rits/MonoScene上获取。

3. Method

三维语义场景补全( 3D Semantic Scene Completion，SSC )旨在通过预测标签 C = { c 0 , c 1 , … , c M } C=\{c_0,c_1,\ldots,c_M\} C={c0​,c1​,…,cM​}，即自由类 $c_0$ 和 $M$ 个语义类，来联合推断三维场景( $\hat{y}$ )的几何和语义。这几乎完全由2.5 D或3D输入来解决[ 56 ]，例如点云、深度或其他，它们充当强几何线索。

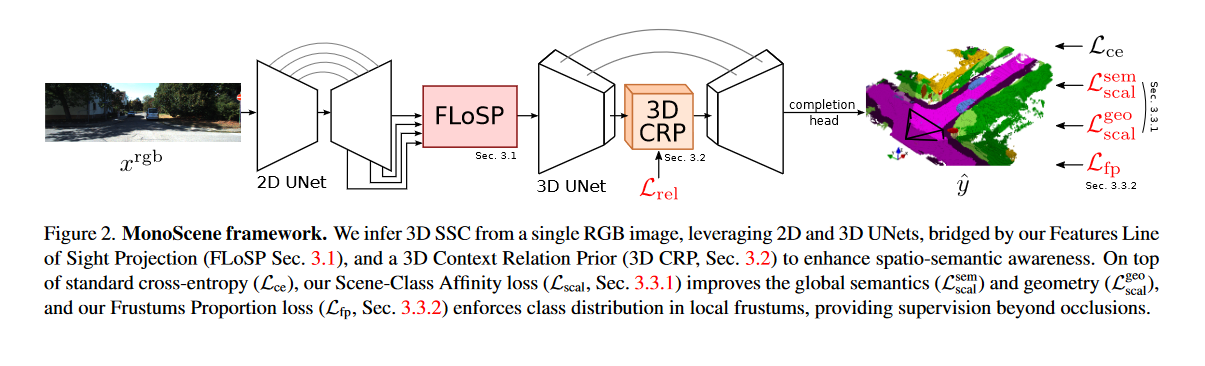
取而代之的是，MonoScene从单幅RGB图像$x^{rgb}$中求解体素级SSC，学习 $\hat{y}=f(x^{\mathrm{rgb}})$ 。这显然是困难的，因为从2D恢复3D是很复杂的。在图2中，我们的流水线使用2D和3D UNets，由我们的特征视线投影模块( FLoSP , Sec。3.1 )桥接，将2D特征提升到合理的3D位置，这促进了信息流，并实现了2D - 3D解耦。受[ 71 ]的启发，我们在3D编码器和解码器之间插入3D Context Relation Prior组件( 3D CRP , Sec . 3.2 )来捕获长距离语义上下文。为了指导SSC训练，我们引入了新的补充损失。首先，场景类亲和性损失( Sec.3.3.1 )优化了类内和类间的场景度量。其次，Frustum Proportion Loss ( Sec.3.3.2 )在局部锥台中对齐类分布，提供了场景遮挡之外的监督。

2D - 3D backbond。我们依靠连续的具有标准跳跃连接的2D和3D UNet。2D UNet基于预训练的EfficientNetB7 [ 61 ]，将图像 $x^{rgb}$ 作为输入。3D UNet是一个2层的自定义浅层编码器解码器。SSC输出 $\hat{y}$ 是通过处理3D UNet输出特征得到的，我们的完井头带有一个3D ASPP [ 7 ]块和一个softmax层。

3.1. Features Line of Sight Projection (FLoSP)

将2D提升到3D是众所周知的不适定问题，因为单视点的尺度模糊[ 22 ]。我们从光学和背面投射多尺度2D特征推理出所有可能的3D对应关系，即沿着它们的光学射线，聚集在一个独特的3D表示中。我们的直觉是，用3D网络处理后者将从2D特征的集合中提供指导。我们的投影机制与文献[ 52 ]类似，但后者将每个2D地图投影到给定的3D地图- -作为2D - 3D跳跃连接。相反，我们的组件通过将多尺度2D特征提升到单个3D特征图来桥接2D和3D网络。我们认为这使得2D - 3D解耦表示成为可能，为3D网络提供了使用高级2D特征进行细粒度3D的自由

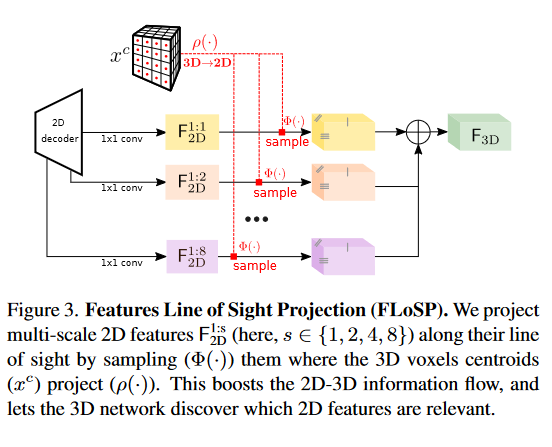
我们的过程如图3所示。在实际应用中，假设相机内参数已知，我们将3D体素质心( $x^c$ )投影到2D，并从尺度为$1:s$的2D解码器特征图 ${\mathsf{F}}_{2D}^{1:\mathsf{s}}$ 中采样相应的特征。重复所有尺度 $S$ 下的过程，写出最终的三维特征图${\mathsf{F}}_{3D}$
$${\mathsf{F}}_{3D}=\sum _{s\in S}{\Phi }_{\rho (x^{\mathrm{c}})}({\mathsf{F}}_{2D}^{1:\mathsf{s}}),$$
其中 ${\Phi }_a(b)$ 是 $b$ 在坐标 $a$ 处的采样$\rho (\cdot )$是透视投影.在实际应用中，我们从尺度 S = { 1 , 2 , 4 , 8 } S = \{ 1,2,4,8 \} S={1,2,4,8}中选择背面投射(backproject)，并在采样前在二维地图上应用1x1 conv进行求和。投射到图像外部的体素其特征向量设置为0。输出图 ${\mathsf{F}}_{3D}$ 作为3D UNet输入。

3.2. 3D Context Relation Prior (3D CRP)

由于SSC高度依赖于上下文[ 56 ]，我们从CPNet [ 71 ]中得到启发，证明了二进制上下文先验对于二维分割的好处。在这里，我们提出了一个3D上下文关系先验( 3D Context Relation Prior，3D CRP )层，插入到3D UNet瓶颈处，该层学习n - way体素-体素语义场景关系图。这给网络提供了一个全局感受野，并由于关系发现机制增加了空间语义感知。

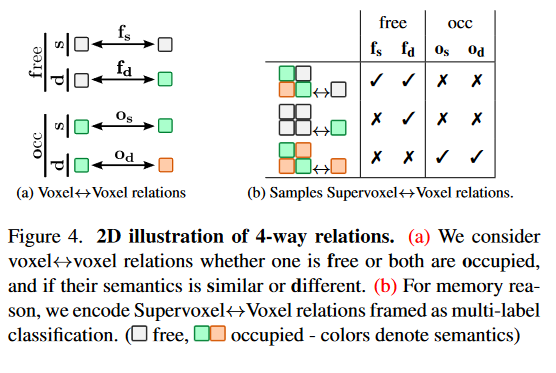
由于SSC是一个高度不平衡的任务，像文献[ 71 ]那样学习二进制(即n = 2 )关系是次优的。取而代之的是考虑n = 4个双侧体素的体素-体素关系，分组为空闲和占用，分别对应"至少一个体素空闲"和"两个体素都占用"。对于每个组，我们对体素语义类是否相似或不同进行编码，得到4个不重叠的关系： M = { f s , f d , o s , o d } \mathcal{M}=\{\mathbf{f_s,f_d,o_s,o_d}\} M={fs​,fd​,os​,od​}。图4a展示了2D (颜色含义见标题)中的关系。

由于体素关系与 $N$ 个体素的 $N^2$ 关系是贪婪的，我们提出了更轻的超体素关系。

Supervoxel↔Voxel relation. 我们将超体素定义为每个 $s^3$ 个相邻体素的非重叠组，并学习更小的超体素-体素关系矩阵，其大小为 $\frac{N^2}{s^3}$。考虑一个超体素 $\mathcal{V}$ 有体素 { ν 1 , … , ν s 3 } \{\nu_{1},\ldots,\nu_{s^{3}}\} {ν1​,…,νs3​} 和一个体素 $\nu$，存在 $s^3$ 对关系 { ν 1 ↔ ν , … , ν s 3 ↔ ν } \{\nu_{1}\leftrightarrow\nu,\ldots,\nu_{s^{3}}\leftrightarrow\nu\} {ν1​↔ν,…,νs3​↔ν}。我们不是回归V Particiv中M关系的复杂计数，而是预测存在哪些M关系，如图4 b所示。这写道，
V ↔ ν = { ν 1 ↔ ν , … , ν s 3 ↔ ν } ≠ \mathcal{V}\leftrightarrow\nu=\{\nu_1\leftrightarrow\nu,\ldots,\nu_{s^3}\leftrightarrow\nu\}_{\neq} V↔ν={ν1​↔ν,…,νs3​↔ν}=​
其中 { ⋅ } ≠ \{\cdot\}\neq {⋅}= 返回集合的不同元素。

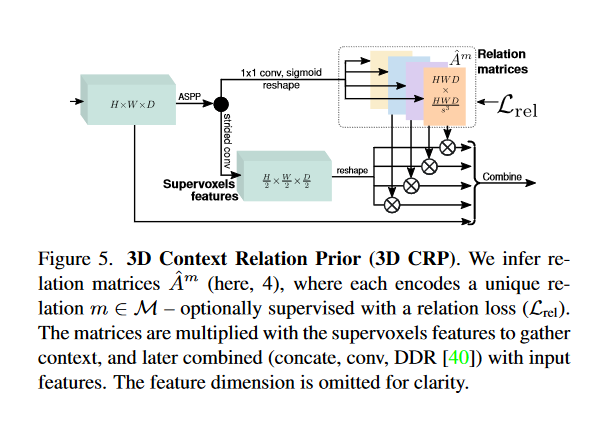
3D Context Relation Prior Layer. 图5说明了我们层的架构。它将空间维度 $H\times W\times D$ 的3D地图作为输入，在其上应用一系列ASPP卷积[7]以收集大的感受野，然后分裂成 $n=|\mathcal{M}|$ 大小为 $HWD\times \frac{HWD}{s^3}$ 的矩阵。

每个矩阵 ${\hat{A}}^m$ 编码一个关系 $m\in M$ ，由其基本真值 $A^m$ 监督。然后，我们优化加权多标签二进制交叉熵损失：
$${\mathcal{L}}_{rel}=-\sum _{m\in \mathcal{M},i}[(1-A_i^m)\log (1-{\hat{A}}_i^m)+w_m{A}_i^m\log {\hat{A}}_i^m]$$
其中 $i$ 循环通过关系矩阵的所有元素，并且 $w_m=\frac{{\sum }_i(1-A_i^m)}{{\sum }_i{A}_i^m}$。关系矩阵与重塑的超体素特征相乘以收集全球上下文。