常微分方程初边值问题数值解
第九章
1. 引言
微分方程 :含有未知函数及其导数或微分的等式;
除了少数特殊类型的微分方程能用解析方法求得精确解外 , 多数情况找不到解的解析表达式
本章研究两类常微分问题: 一阶常微分方程的初值问题 ; 两阶常微分方程边值问题
- 一阶常微分方程的初值问题
{ y ′ = f ( x , y ) , x ∈ [ a , b ] , y ( a ) = y 0 , \left.\left\{\begin{array}{ll}\boldsymbol{y}'=\boldsymbol{f}(x,\boldsymbol{y}),&\quad x\in[a,b],\\\boldsymbol{y}(\boldsymbol{a})=\boldsymbol{y}_0,\end{array}\right.\right. {y′=f(x,y),y(a)=y0,x∈[a,b],
y ( x ) y(x) y(x) 是定义在 [a,b] 上的 m 维函数向量; f ( x , y ) f(x,y) f(x,y) 是定义在 m + 1 维区域 G = { ( x , y ) ∣ x ∈ [ a , b ] , y ∈ R m } G=\{(x,\boldsymbol{y})\mid x\in[a,b],\boldsymbol{y}\in\mathbb{R}^m\} G={(x,y)∣x∈[a,b],y∈Rm} 上的 m 维已知函数向量.
由常微分方程理论知:如果函数 f(x,y) 在区域 G 中连续 , 且关于y 满足利普希茨 (Lipschitz) 条件 , 即对所有 x ∈ [ a , b ] 及 y ∈ R m , z ∈ R m , x\in[a,b]\text{ 及 }y\in\mathbb{R}^m, z\in\mathbb{R}^m, x∈[a,b] 及 y∈Rm,z∈Rm, 总存在常数 L > 0,使得:
∥ f ( x , y ) − f ( x , z ) ∥ ⩽ L ∥ y − z ∥ , \|f(x,y)-f(x,z)\|\leqslant L\|y-z\|, ∥f(x,y)−f(x,z)∥⩽L∥y−z∥,
则方程 (9.1) 存在唯一解 , 且解连续依赖于初始条件和右端项
- 两阶常微分方程边值问题
{ − y ′ ′ + q ( x ) y = f ( x ) , x ∈ [ a , b ] , y ( a ) = α , y ( b ) = β , \begin{cases}&-y''+q(x)y=f(x),\quad x\in[a,b],\\&y(a)=\alpha, y(b)=\beta,\end{cases} {−y′′+q(x)y=f(x),x∈[a,b],y(a)=α,y(b)=β,
其中 q ( x ) q(x) q(x) 和 f ( x ) f(x) f(x) 在区间 [a,b] 上连续 , q(x) > 0. 这里假设上述边值问题存在唯一解 , 且解连续依赖于边界条件和右端项
- 总结
无论是初值问题还是边值问题 , 其解 y = y ( x ) \boldsymbol{y}=\boldsymbol{y}(x) y=y(x) 都是区间 [a,b] 上关于变量 x 的函数或函数向量, y = ( y 1 ( x ) , y 2 ( x ) , ⋯ , y m ( x ) ) T \boldsymbol{y}=(y_1(x),y_2(x),\cdots,y_m(x))^T y=(y1(x),y2(x),⋯,ym(x))T. 记 a = x 0 < x 1 < ⋯ < x N − 1 < x N = b a=x_{0}<x_{1}<\cdots<x_{N-1}<x_{N}=b a=x0<x1<⋯<xN−1<xN=b 为求解区域中的一系列节点 . 数值解就是要计算精确解 y ( x ) \boldsymbol{y(x)} y(x) 在这些节点 x n x_n xn 处的近似值 y n \boldsymbol{y_n} yn .
为了简单起见,假设网格点为均匀网格:
h n = x n + 1 − x n = h = b − a N , h_n=x_{n+1}-x_n=h=\frac{b-a}{N}, hn=xn+1−xn=h=Nb−a,
h为网格步长,本文主要介绍 m = 1 时的初值问题 , 对于边值问题和 m > 1 的情况下的初值问题将分别在最后两节作简单介绍
2.欧拉公式(欧拉折线法)
初值问题:
{ y ′ = f ( x , y ) , x ∈ [ a , b ] , y ( a ) = y 0 , (1) \left.\left\{\begin{array}{ll}\boldsymbol{y}'=\boldsymbol{f}(x,\boldsymbol{y}),&\quad x\in[a,b],\\\boldsymbol{y}(\boldsymbol{a})=\boldsymbol{y}_0,\end{array}\right.\right.\tag{1} {y′=f(x,y),y(a)=y0,x∈[a,b],(1)
欧拉公式是求解初值问题 公式(1) 的一种简单而古老的数值方法 .
- 基本思路
把方程(1) 中的导数项 y ′ \boldsymbol{y'} y′ 用差商逼近 , 从而把一个微分方程转化成为一个代数方程 , 以便求解.
在节点 x n x_n xn处, 公式(1)有:
y ′ ( x n ) = f ( x n , y ( x n ) ) . y'(x_n)=f(x_n,y(x_n)). y′(xn)=f(xn,y(xn)).
y ′ y' y′有三种差商公式:前向差商, 后向差商, 中间差商.以下以前向差商为例:
y ′ ( x n ) ≈ y ( x n + 1 ) − y ( x n ) x n + 1 − x n , y'(x_n)\approx\frac{y(x_{n+1})-y(x_n)}{x_{n+1}-x_n}, y′(xn)≈xn+1−xny(xn+1)−y(xn),
则得到离散公式:
y ( x n + 1 ) ≈ y ( x n ) + ( x n + 1 − x n ) f ( x n , y ( x n ) ) . (1.1) y(x_{n+1})\approx y(x_{n})+(x_{n+1}-x_n)f(x_{n},y(x_{n})).\tag{1.1} y(xn+1)≈y(xn)+(xn+1−xn)f(xn,y(xn)).(1.1)
因为真解 y(x) 是未知的, 所以用近似解 y(x_n) 来逼近真解.只要知道初值 y ( a ) = y 0 y(a)=y_0 y(a)=y0, 就可以用欧拉公式来求解出 y ( x i ) , i = 1 , 2 , ⋯ , n y(x_i),i=1,2,\cdots,n y(xi),i=1,2,⋯,n的数值解.
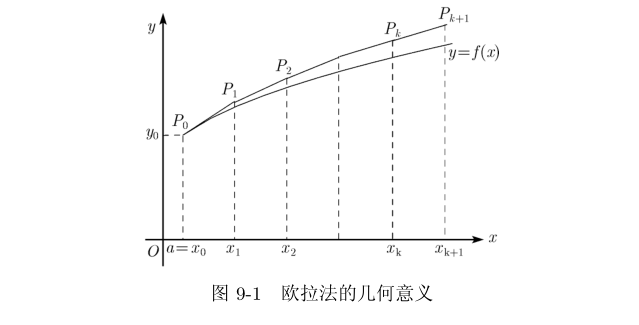
欧拉公式的几何意义十分清楚,方程 y ′ = f ( x , y ) y' = f(x,y) y′=f(x,y) 满足初始条件 y ( x 0 ) = y 0 y(x_0 ) = y _0 y(x0)=y0 的解y = y(x) 是 xOy 平面上过点 P 0 ( x 0 , y 0 ) P_0 (x_0 ,\boldsymbol{y_0}) P0(x0,y0) 的一条特殊积分曲线.欧拉方法就是用从 P 0 P_0 P0 出发的折线 P 0 , P 1 ⋅ ⋅ ⋅ P N P_0, P_1 ···P_N P0,P1⋅⋅⋅PN 来作为积分曲线 y = y(x) 的近似解

2.1 例题

精确解: y ( x ) = 1 + 2 x y(x)=\sqrt{1+2x} y(x)=1+2x
# -*- coding: utf-8 -*-
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
def f(x,y)->float:
return y-2*x/y
y0,a,b,n=1,0,1,10
def y(x)->float:
return np.sqrt(1+2*x)
xi,yi=EulerMethod(f,y0,a,b,n)
plt.plot(xi,yi,label='Euler Method')
plt.plot(xi,[y(i) for i in xi],label='Exact Solution')
plt.legend()
plt.show()
plt.plot(xi,[abs(yi[i]-y(xi[i])) for i in range(len(yi))],label='Absolute Error')
plt.legend()
plt.show()
- 数值解和精确解的对比
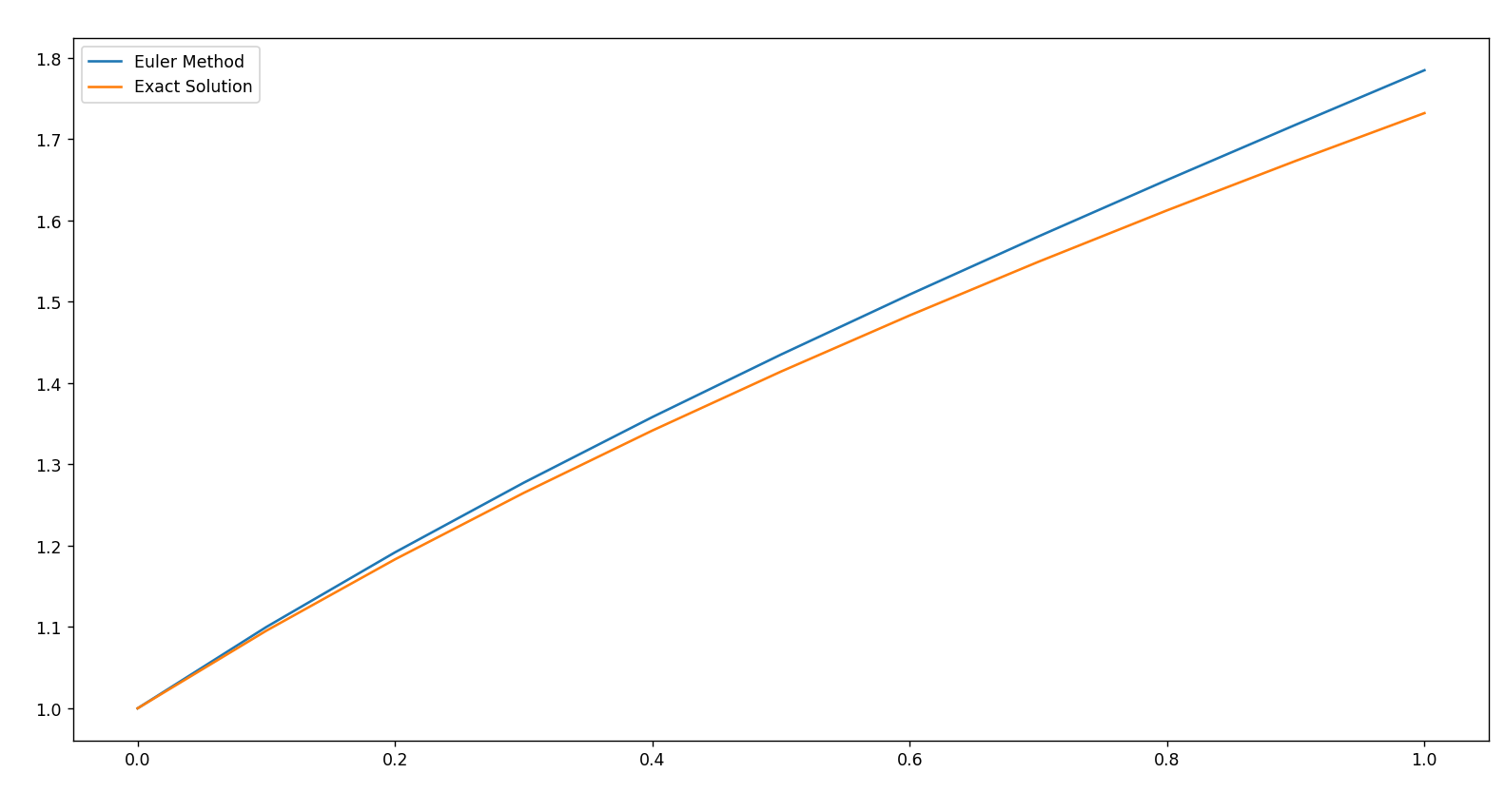
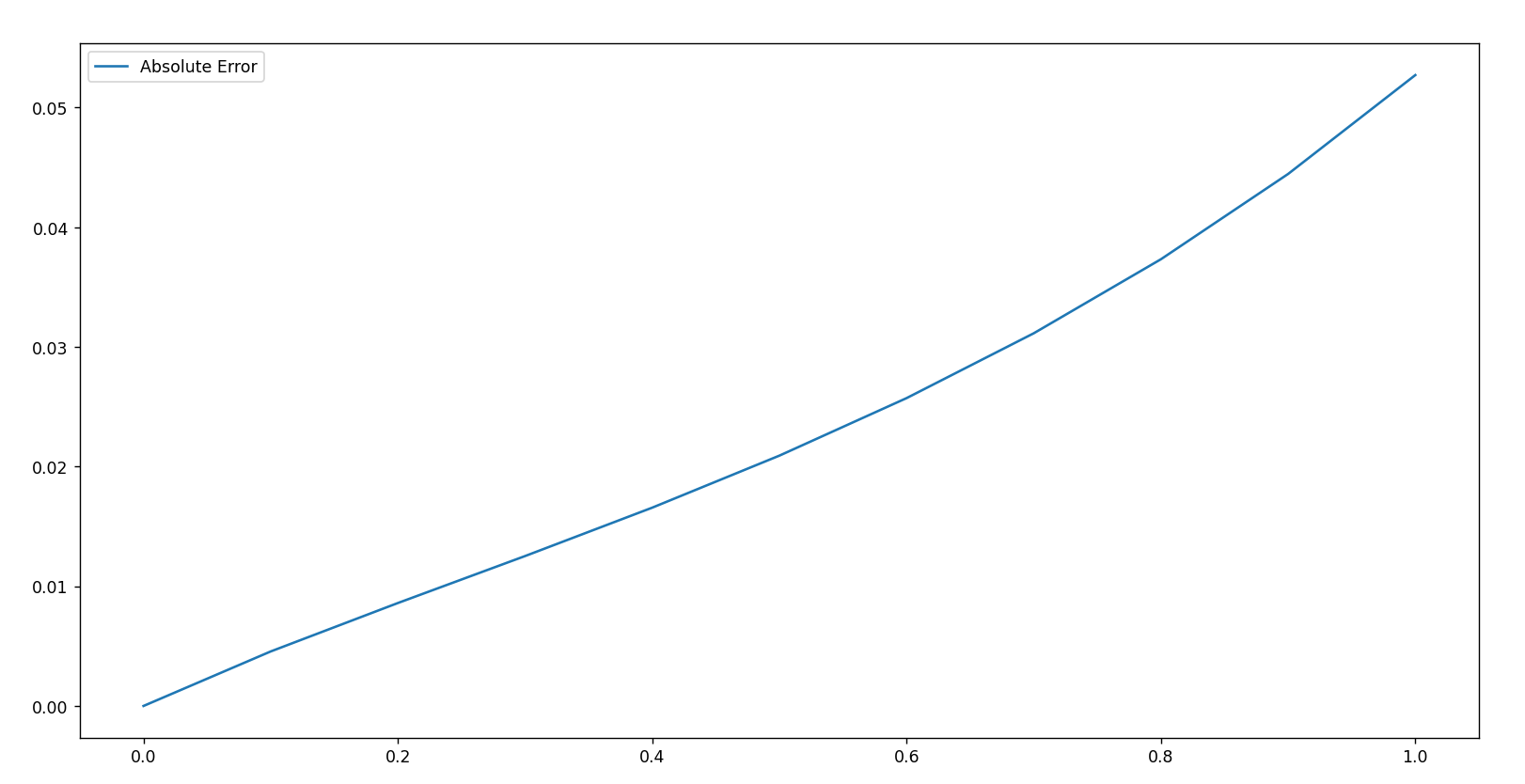
两者相比较 , 显然欧拉方法给出的数值解误差较大 , 一般只有两位有效数字
3. 欧拉公式的改进
从另一角度来考察初值问题,(1) 式改写为:
d y ( x ) = f ( x , y ( x ) ) d x . (2) \mathrm{d}y(x)=f(x,y(x))\mathrm{d}x.\tag{2} dy(x)=f(x,y(x))dx.(2)
令积分区间为 [ x n , x n + 1 ] [x_n,x_{n+1}] [xn,xn+1],则有:
y ( x n + 1 ) = y ( x n ) + ∫ x n x n + 1 f ( x , y ( x ) ) d x . y(x_{n+1})=y(x_n)+\int_{x_n}^{x_{n+1}}f(x,y(x))\mathrm{d}x. y(xn+1)=y(xn)+∫xnxn+1f(x,y(x))dx.
积分式如下:
∫ x n x n + 1 f ( x , y ( x ) ) d x . (3) \int_{x_n}^{x_{n+1}}f(x,y(x))\mathrm{d}x.\tag{3} ∫xnxn+1f(x,y(x))dx.(3)
对于右端的积分式子,其中含有位置函数y(x),无法直接计算,可以采用数值积分的方法计算其近似值.将初值问题方程 (1) 离散化的方法称为初值问题的数值积分方法
使用不同的数值积分公式,会有不同的计算公式
若采用左矩形积分公式,则:
∫ x n x n + 1 f ( x , y ( x ) ) d x ≈ h f ( x n , y ( x n ) ) . \int_{x_n}^{x_{n+1}}f(x,y(x))\mathrm{d}x\approx hf(x_n,y(x_n)). ∫xnxn+1f(x,y(x))dx≈hf(xn,y(xn)).
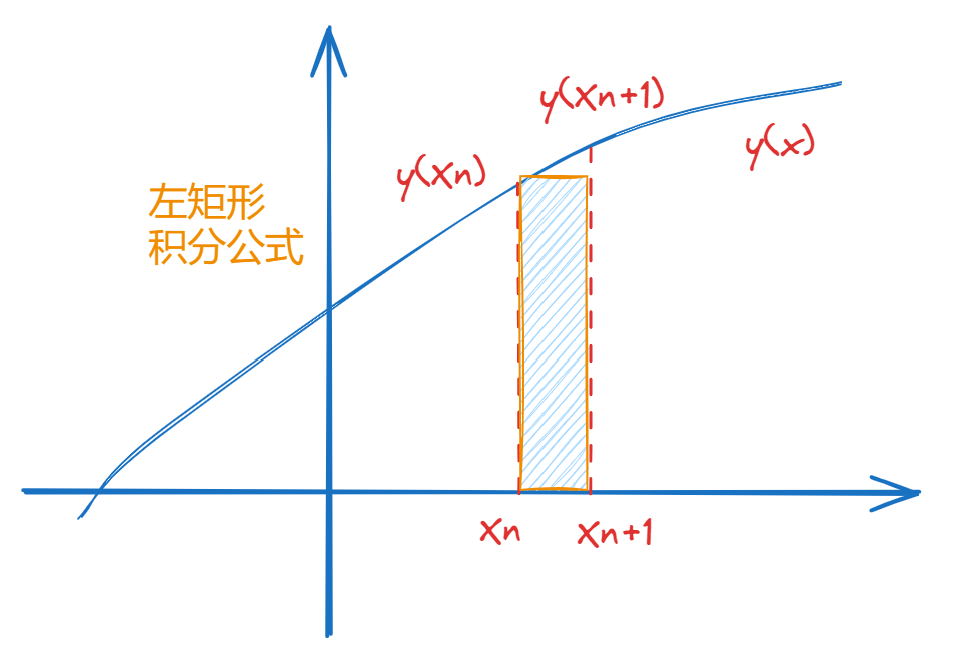
则可以得到欧拉公式:
y ( x n + 1 ) ≈ y ( x n ) + h f ( x n , y ( x n ) ) . y(x_{n+1})\approx y(x_n)+hf(x_n, y(x_n)). y(xn+1)≈y(xn)+hf(xn,y(xn)).
3.1 后退欧拉公式
采用右矩形积分公式,有:
∫ x n x n + 1 f ( x , y ( x ) ) d x ≈ h f ( x n + 1 , y ( x n + 1 ) ) . \int_{x_n}^{x_{n+1}}f(x,y(x))\mathrm{d}x\approx hf(x_{n+1},y(x_{n+1})). ∫xnxn+1f(x,y(x))dx≈hf(xn+1,y(xn+1)).
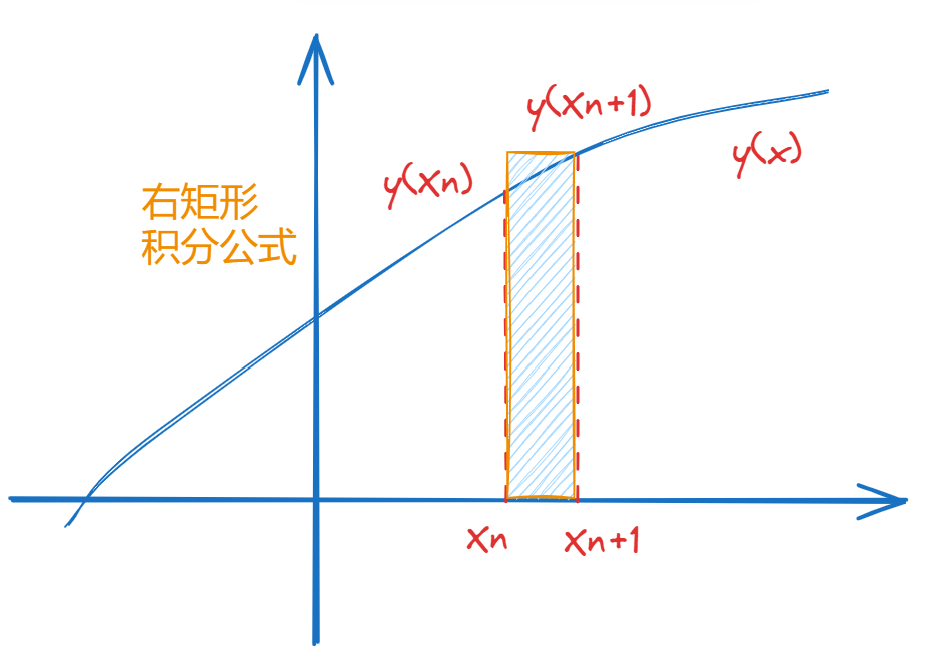
则可以得到后退欧拉公式:
y n + 1 = y n + h f ( x n + 1 , y n + 1 ) . y_{n+1}=y_n+hf(x_{n+1},y_{n+1}). yn+1=yn+hf(xn+1,yn+1).
3.2 改进欧拉方法-梯形积分
采用梯形积分公式计算公式(3),有:
∫ x n x n + 1 f ( x , y ( x ) ) d x ≈ h 2 ( f ( x n , y ( x n ) ) + f ( x n + 1 , y ( x n + 1 ) ) ) \int_{x_n}^{x_{n+1}}f(x,y(x))\mathrm{d}x \approx \frac{h}{2}(f(x_n,y(x_n))+f(x_{n+1},y(x_{n+1}))) ∫xnxn+1f(x,y(x))dx≈2h(f(xn,y(xn))+f(xn+1,y(xn+1)))
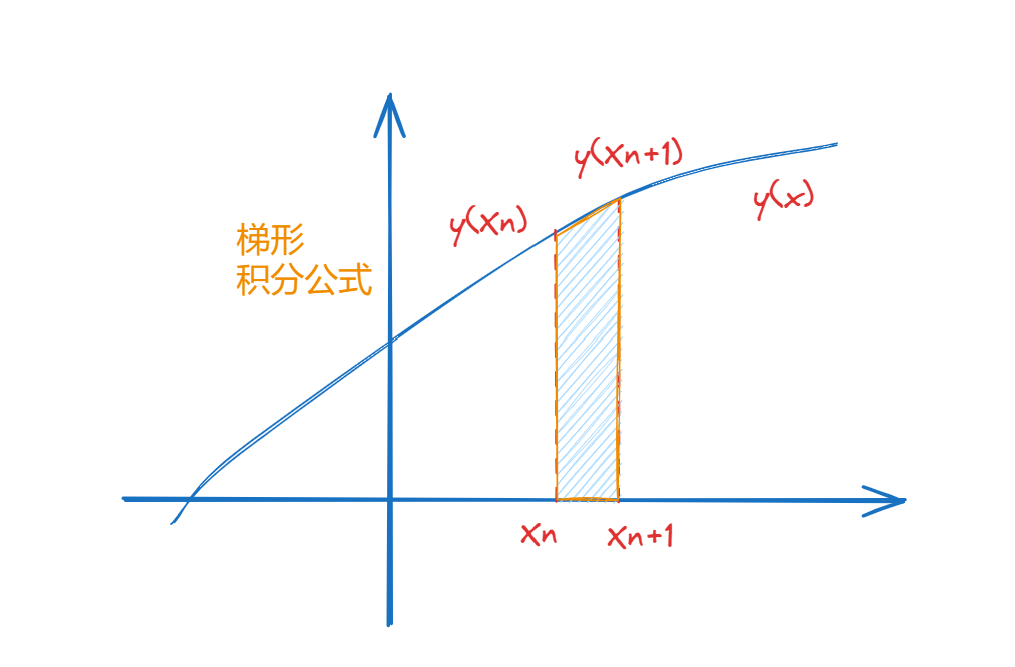
代入公式(2),则有:
y n + 1 = y n + h 2 ( f ( x n , y n ) + f ( x n + 1 , y n + 1 ) ) . (4) y_{n+1}=y_n+\frac h2(f(x_n,y_n)+f(x_{n+1},y_{n+1})).\tag{4} yn+1=yn+2h(f(xn,yn)+f(xn+1,yn+1)).(4)
梯形求积公式比矩形求积公式的代数精度高,因此改进欧拉方法-梯形积分比公式(1.1)精度更高

- 使用梯形公式计算例题9.1.2
...
# 使用梯形公式计算
def TrapeEuler(f,y0,a,b,n,tol:float=1e-10):
"""梯形欧拉公式求解常微分方程"""
h=(b-a)/n
xi=[a+i*h for i in range(n+1)]
yi=np.zeros(n+1)
yi[0]=y0
for i in range(1,n+1):
# 循环迭代
yt0=yi[i-1]
while True:
# 计算t+1的y_{n+1}近似值
yt_next=yi[i-1]+0.5*h*f(xi[i-1],yt0)+0.5*h*f(xi[i],yt0)
# 计算误差
err=abs(yt_next-yt0)
if err<tol:
yi[i]=yt_next
break
else:
yt0=yt_next
return xi,yi
...
ns=[10,50,100,200]
xi20,yi20=TrapeEuler(f,y0,a,b,ns[0])
plt.plot(xi20,yi20,label=f'Trapezoidal Euler Method-h={(b-a)/(ns[0])}',marker='*')
xi21,yi21=TrapeEuler(f,y0,a,b,ns[1])
plt.plot(xi21,yi21,label=f'Trapezoidal Euler Method-h={(b-a)/(ns[1])}',marker='*')
xi22,yi22=TrapeEuler(f,y0,a,b,ns[2])
plt.plot(xi22,yi22,label=f'Trapezoidal Euler Method-h={(b-a)/(ns[2])}',marker='*')
xi23,yi23=TrapeEuler(f,y0,a,b,ns[3])
plt.plot(xi23,yi23,label=f'Trapezoidal Euler Method-h={(b-a)/(ns[3])}',marker='*')
....
plt.plot(xi20,[abs(yi20[i]-y(xi20[i])) for i in range(len(yi20))],label=f'trapezoidal-Improve Euler Method-h={(b-a)/ns[0]}')
plt.plot(xi21,[abs(yi21[i]-y(xi21[i])) for i in range(len(yi21))],label=f'trapezoidal-Improve Euler Method-h={(b-a)/ns[1]}')
plt.plot(xi22,[abs(yi22[i]-y(xi22[i])) for i in range(len(yi22))],label=f'trapezoidal-Improve Euler Method-h={(b-a)/ns[2]}')
plt.plot(xi23,[abs(yi23[i]-y(xi23[i])) for i in range(len(yi23))],label=f'trapezoidal-Improve Euler Method-h={(b-a)/ns[3]}')
...
不同的步长h对数值解的影响:
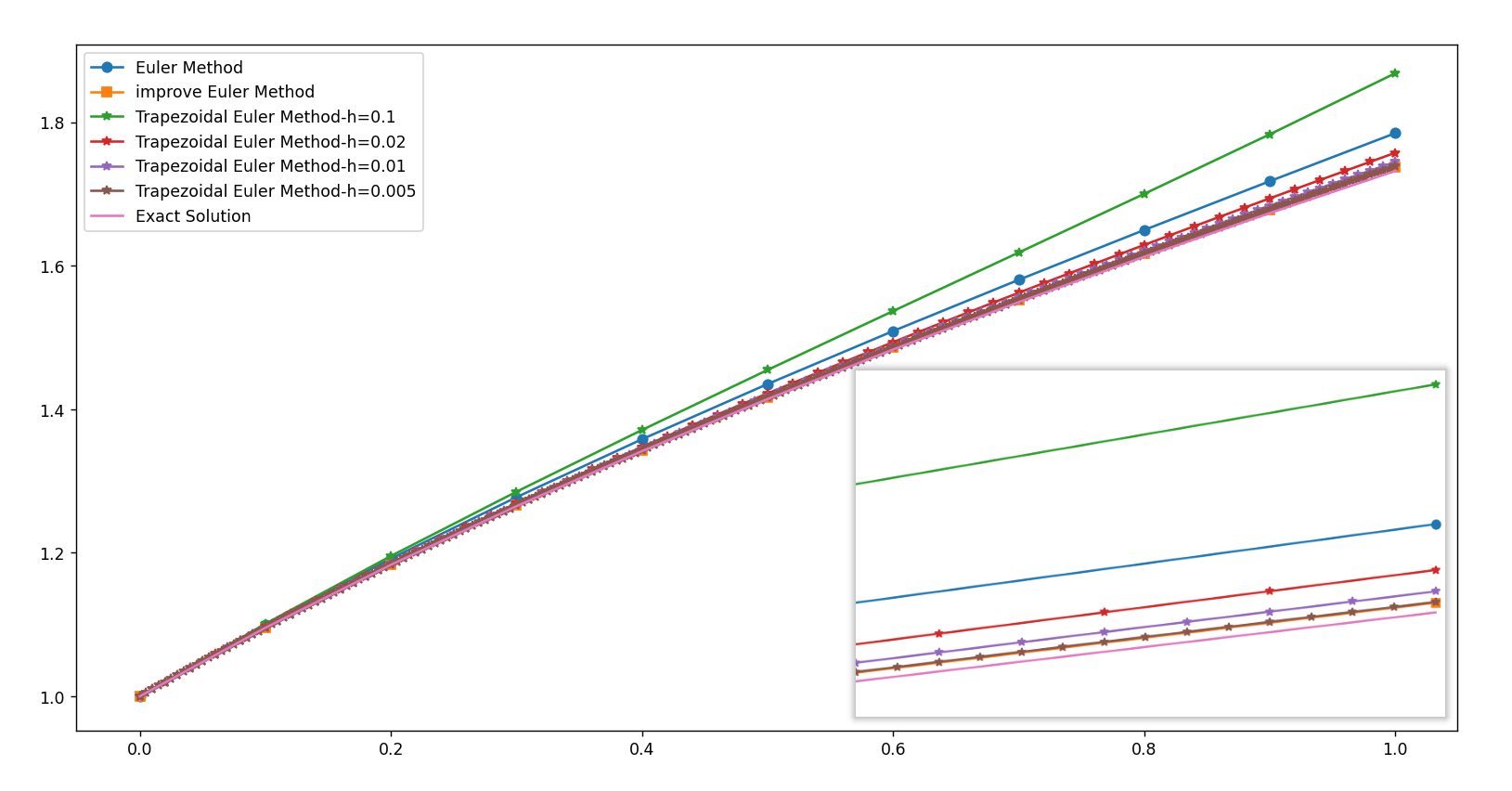
不同步长h对数值解的误差:h->0时,误差趋于0.可以发现梯形公式的误差最后趋向于改进欧拉公式的误差
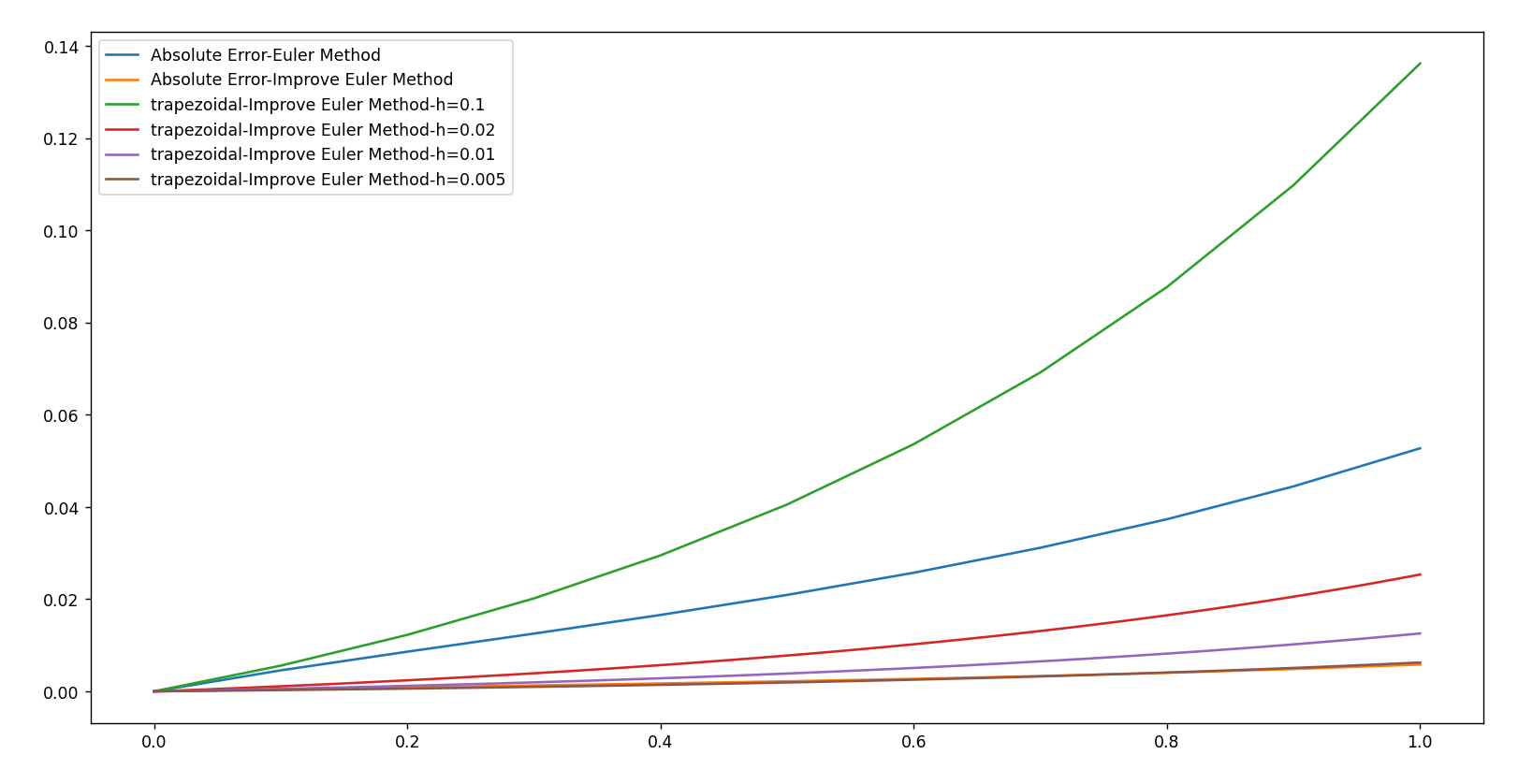
3.3 利用高阶数值积分的离散格式
- 亚当斯 – 巴什福思 (Adams-Bashforth) 公式
y n + 1 = y n + h 24 ( 55 f ( x n , y n ) − 59 f ( x n − 1 , y n − 1 ) + 37 f ( x n − 2 , y n − 2 ) − 9 f ( x n − 3 , y n − 3 ) ) . y_{n+1}=y_{n}+\frac{h}{24}(55f(x_{n},y_{n})-59f(x_{n-1},y_{n-1})+37f(x_{n-2},y_{n-2})-9f(x_{n-3},y_{n-3})). yn+1=yn+24h(55f(xn,yn)−59f(xn−1,yn−1)+37f(xn−2,yn−2)−9f(xn−3,yn−3)).
- 亚当斯 – 莫尔顿 (Adams-Moulton) 公式
y n + 1 = y n + h 24 ( 9 f ( x n + 1 , y n + 1 ) + 19 f ( x n , y n ) − 5 f ( x n − 1 , y n − 1 ) + f ( x n − 2 , y n − 2 ) ) . y_{n+1}=y_n+\frac{h}{24}(9f(x_{n+1},y_{n+1})+19f(x_n,y_n)-5f(x_{n-1},y_{n-1})+f(x_{n-2},y_{n-2})). yn+1=yn+24h(9f(xn+1,yn+1)+19f(xn,yn)−5f(xn−1,yn−1)+f(xn−2,yn−2)).
欧拉公式与梯形公式只需 y n y_n yn就可以计算 y n + 1 y_{n+1} yn+1,称为单步法
亚当斯 – 巴什福思公式与亚当斯 – 莫尔顿公式计算 y n + 1 y_{n+1} yn+1 时 , 除了要知道 y n y_n yn 外 , 还需知道 y n − 1 , y n − 2 y_{n−1} , y_{n−2} yn−1,yn−2 等 , 这类公式称为多步法
对于欧拉公式和亚当斯 – 巴什福思公式这类,右端不含有 y n + 1 y_{n+1} yn+1的方法,称为显式格式
对于梯形公式与亚当斯 – 莫尔顿公式的右端隐含 y n + 1 y_n+1 yn+1,计算 y n + 1 y_{n+1} yn+1需要求解非线性方程的方法,称为隐式格式
3.4 局部截断误差
局部截断误差可用于表征求解初值问题的数值方法的计算精度.
一般地 , 常微分方程初值问题的数值解满足形如:
y n + 1 = y n + h g ( y n + 1 , y n , ⋯ , y n − r ) y_{n+1}=y_n+hg(y_{n+1},y_n,\cdots,y_{n-r}) yn+1=yn+hg(yn+1,yn,⋯,yn−r)
的等式 , 其中 y n , ⋯ , y n − r 为 y 在 r + 1 个节点 x n , ⋯ , x n − r 处的数值解 . y_{n},\cdots,y_{n-r}\text{ 为 }y\text{ 在 }r+1\text{ 个节点 }x_{n},\cdots,x_{n-r}\text{ 处的数值解}. yn,⋯,yn−r 为 y 在 r+1 个节点 xn,⋯,xn−r 处的数值解.
数值方法的局部截断误差为:
ε n + 1 = y ( x n + 1 ) − y ( x n ) − h g ( y ( x n + 1 ) , y ( x n ) , ⋯ , y ( x n − r ) ) , \varepsilon_{n+1}=y(x_{n+1})-y(x_n)-hg(y(x_{n+1}),y(x_n),\cdots,y(x_{n-r})), εn+1=y(xn+1)−y(xn)−hg(y(xn+1),y(xn),⋯,y(xn−r)),
真解与近似解之间的差异 ε n = y ( x n ) − y n \varepsilon_n = y(x_n ) − y_n εn=y(xn)−yn 称为数值方法的整体截断误差

3.5 预估校正格式(改进欧拉算法)
梯形方法公式(4)比欧拉公式(1.1)精度得到提升,但计算量大增.一种有效简化计算的方法是:当h较小时,先使用显式格式计算合适的预估值
y
n
+
1
ˉ
\bar{y_{n+1}}
yn+1ˉ,
后利用隐式格式迭代一二次计算校正值
y
n
+
1
y_{n+1}
yn+1.称为预估校正方法
- 一阶预估二阶校正公式
其中一种预估校正公式是:
{ 预估 y n + 1 ‾ = y n + h f ( x n , y n ) , 校正 y n + 1 = y n + h 2 ( f ( x n , y n ) + f ( x n + 1 , y n + 1 ‾ ) (5) \begin{cases}&\text{预估}\quad \overline{y_{n+1}}=y_n+hf(x_n,y_n),\\&\text{校正}\quad y_{n+1}=y_n+\frac{h}{2}(f(x_n,y_n)+f(x_{n+1},\overline{y_{n+1}})\end{cases}\tag{5} {预估yn+1=yn+hf(xn,yn),校正yn+1=yn+2h(f(xn,yn)+f(xn+1,yn+1)(5)
通常称为改进的欧拉公式,另一种表示为:
y n + 1 = y n + h 2 ( f ( x n , y n ) + f ( x n + h , y n + h f ( x n , y n ) ) ) y_{n+1}=y_n+\frac{h}{2}\left(f(x_n,y_n)+f(x_n+h,y_n+hf(x_n,y_n))\right) yn+1=yn+2h(f(xn,yn)+f(xn+h,yn+hf(xn,yn)))

改进欧拉方法精度高于欧拉公式,但小于梯形公式.计算量远小于梯形公式.
一般地 , 较为简单的预估校正格式都包含两个计算公式 , 一个是显式公式 , 作为预估公式 ; 另一个是隐式公式 , 作为校正公式 , 当然也可以构造包含多个计算公式的预估校正格式
构造预估校正格式时 , 应该注意阶数的匹配, 例如在式 (5) 中 , 校正公式具有二阶精度 , 而预估公式仅具有一阶精度 . 因为提供的预估精度较差 , 且仅经一次校正 , 校正值的精度不会太高
3.5.1 python 代码实现
- 使用改进欧拉公式计算例题9.1.2
# -*- coding: utf-8 -*-
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
def f(x,y)->float:
return y-2*x/y
y0,a,b,n=1,0,1,10
def y(x)->float:
return np.sqrt(1+2*x)
xi,yi=EulerMethod(f,y0,a,b,n)
plt.plot(xi,yi,label='Euler Method')
xi1,yi1=ImproveEulerMethod(f,y0,a,b,n)
plt.plot(xi1,yi1,label='improve Euler Method')
plt.plot(xi,[y(i) for i in xi],label='Exact Solution')
plt.legend()
plt.show()
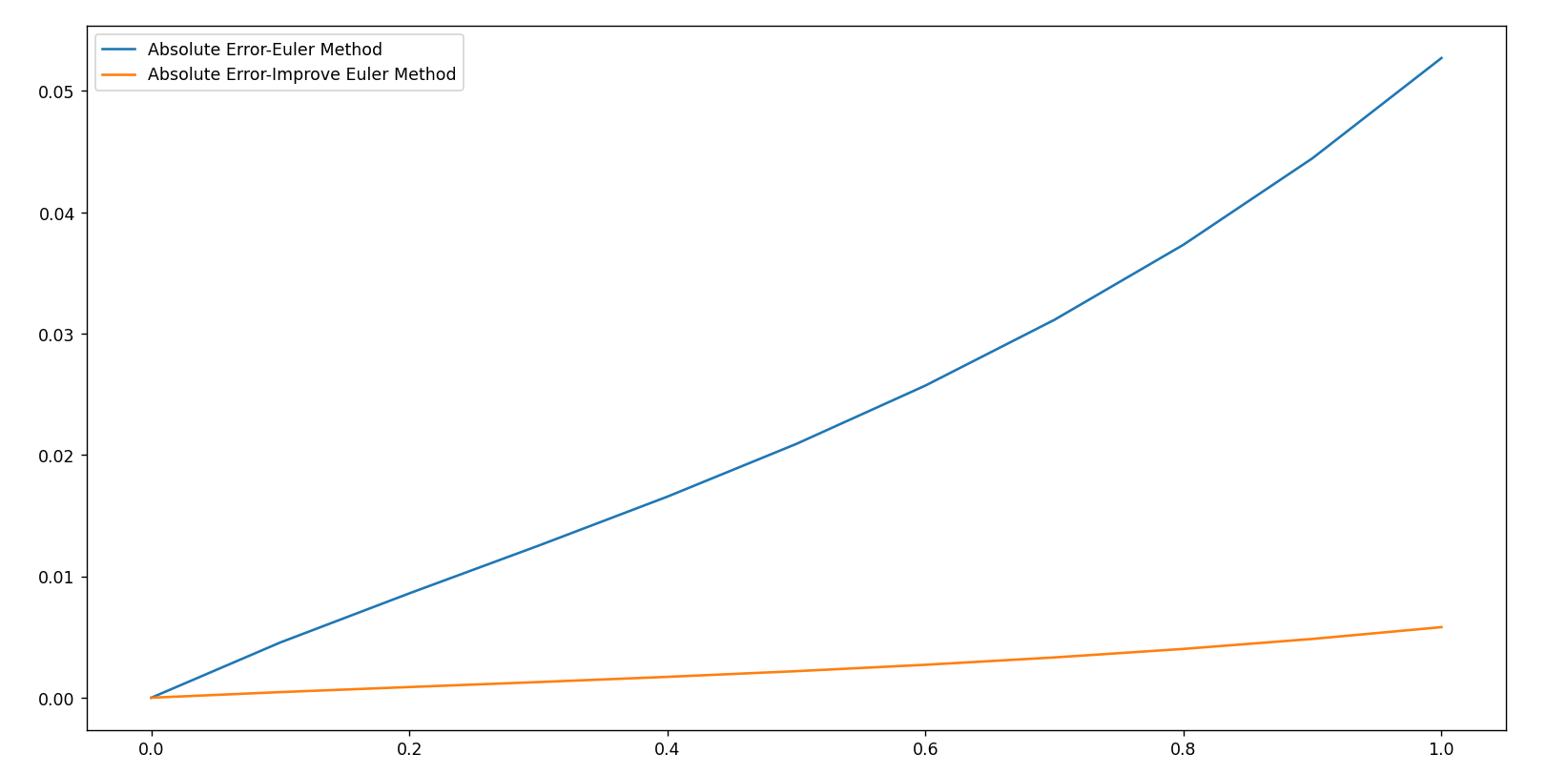
plt.plot(xi,[abs(yi[i]-y(xi[i])) for i in range(len(yi))],label='Absolute Error-Euler Method')
plt.plot(xi1,[abs(yi1[i]-y(xi1[i])) for i in range(len(yi))],label='Absolute Error-Improve Euler Method')
plt.legend()
plt.show()
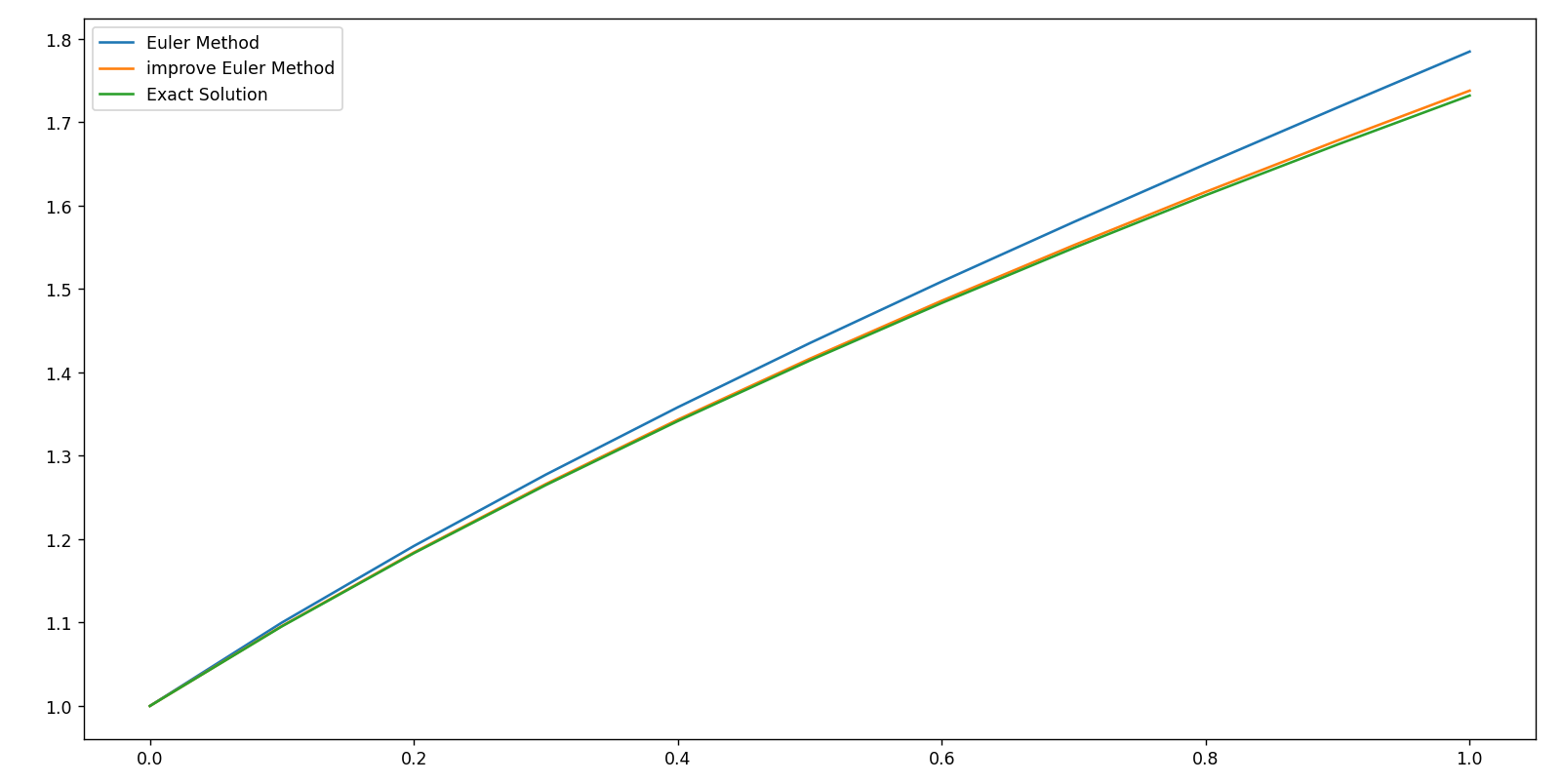
算法误差对比
- 二阶预估二阶校正格式
{ 预估 y n + 1 ‾ = y n − 1 + 2 h f ( x n , y n ) , 校正 y n + 1 = y n + h 2 ( f ( x n , y n ) + f ( x n + 1 , y n + 1 ‾ ) ) (6) \left.\left\{\begin{array}{ll}\text{预估}&\overline{y_{n+1}}=y_{n-1}+2hf(x_n, y_n),\\\\\text{校正}&y_{n+1}=y_n+\frac{h}{2}(f(x_n,y_n)+f(x_{n+1}, \overline{y_{n+1}}))\end{array}\right.\right.\tag{6} ⎩ ⎨ ⎧预估校正yn+1=yn−1+2hf(xn,yn),yn+1=yn+2h(f(xn,yn)+f(xn+1,yn+1))(6)
公式(6)的预估公式/校正公式都具有二阶精度 , 因此精度更高.
- 四阶亚当斯预估校正系统
{ y n + 1 ‾ = y n + h 24 ( 55 f ( x n , y n ) − 59 f ( x n − 1 , y n − 1 ) + 37 f ( x n − 2 , y n − 2 ) − 9 f ( x n − 3 , y n − 3 ) ) , y n + 1 = y n + h 24 ( 9 f ( x n + 1 , y n + 1 ‾ ) + 19 f ( x n , y n ) − 5 f ( x n − 1 , y n − 1 ) + f ( x n − 2 , y n − 2 ) ) . (7) \begin{cases}\overline{y_{n+1}}=y_{n}+\frac{h}{24}(55f(x_{n},y_{n})-59f(x_{n-1},y_{n-1})+37f(x_{n-2},y_{n-2})-9f(x_{n-3},y_{n-3})),\\\\y_{n+1}=y_{n}+\frac{h}{24}(9f(x_{n+1},\overline{y_{n+1}})+19f(x_{n},y_{n})-5f(x_{n-1},y_{n-1})+f(x_{n-2},y_{n-2})).\end{cases}\tag{7} ⎩ ⎨ ⎧yn+1=yn+24h(55f(xn,yn)−59f(xn−1,yn−1)+37f(xn−2,yn−2)−9f(xn−3,yn−3)),yn+1=yn+24h(9f(xn+1,yn+1)+19f(xn,yn)−5f(xn−1,yn−1)+f(xn−2,yn−2)).(7)
公式(7)的预估公式/校正公式都具有四阶精度 , 因此精度更高.
4.龙格 – 库塔公式( R-K 方法)
这是一种广泛应用的高精度显式单步法.
龙格 – 库塔公式的基本思想就是设法计算 f(x,y) 在某些点上的函数值 , 然后对这些函数值作线性组合 , 构造近似计算公式 , 再把近似公式和解的泰勒展开式相比较 , 使前面的若干项吻合 , 从而获得达到一定精度的数值计算公式 .
一般的显式龙格 – 库塔公式的形式为:
y n + 1 = y n + ∑ i = 1 r ω i k i k 1 = h f ( x n , y n ) , k i = h f ( x n + α i h , y n + ∑ j = 1 i − 1 β i j k j ) , i = 2 , 3 , ⋯ , r . (8) \begin{aligned}&y_{n+1}=y_{n}+\sum_{i=1}^{r}\omega_{i}k_{i}\\&k_{1}=hf(x_{n},y_{n}),\\&k_{i}=hf\left(x_{n}+\alpha_{i}h,y_{n}+\sum_{j=1}^{i-1}\beta_{ij}k_{j}\right),\quad i=2,3,\cdots,r.\end{aligned}\tag{8} yn+1=yn+i=1∑rωikik1=hf(xn,yn),ki=hf(xn+αih,yn+j=1∑i−1βijkj),i=2,3,⋯,r.(8)
其中 ω i \omega_i ωi, α i \alpha_i αi 和 β i j \beta_{ij} βij 是参数,与公式(1)右端得到f(x,y)及步长h无关. 上式成为r段的龙格 – 库塔公式.特别地 , 若式 (8) 与 y ( x n + 1 ) y(x_{n+1} ) y(xn+1) 的泰勒展开式的前 p + 1项完全一致 , 即局部截断误差达到 O ( h p + 1 ) O(h^{p+1} ) O(hp+1), 则称公式 (8) 为 p阶r段龙格–库塔公式
龙格 – 库塔公式是一类公式 , 每确定一组特殊的系数 , 就得到一个特殊的龙格 – 库塔公式
<<现代数值计算 第二版>>p226页给出了一个二阶二段的龙格 – 库塔公式推导过程,这里不再赘述.
4.1常用的R-K公式
4.1.1二阶二段龙格 – 库塔公式(R-K22)
{ y n + 1 = y n + 1 2 k 1 + 1 2 k 2 , k 1 = h f ( x n , y n ) , k 2 = h f ( x n + h , y n + k 1 ) . (9.1) \begin{cases}&y_{n+1}=y_n+\frac{1}{2}k_1+\frac{1}{2}k_2,\\&k_1=hf(x_n,y_n),\\&k_2=hf(x_n+h,y_n+k_1).\end{cases}\tag{9.1} ⎩ ⎨ ⎧yn+1=yn+21k1+21k2,k1=hf(xn,yn),k2=hf(xn+h,yn+k1).(9.1)
这就是前面的预估校正公式
{ y n + 1 = y n + k 2 , k 1 = h f ( x n , y n ) , k 2 = h f ( x n + 1 2 h , y n + 1 2 k 1 ) . (9.2) \begin{cases}&y_{n+1}=y_n+k_2,\\&k_1=hf(x_n,y_n),\\&k_2=hf\left(x_n+\frac{1}{2}h,y_n+\frac{1}{2}k_1\right).\end{cases}\tag{9.2} ⎩ ⎨ ⎧yn+1=yn+k2,k1=hf(xn,yn),k2=hf(xn+21h,yn+21k1).(9.2)
该格式称为中点公式 .
4.1.2 三阶三段龙格 – 库塔公式(R-K33)
y n + 1 = y n + 1 6 ( k 1 + 4 k 2 + k 3 ) , k 1 = h f ( x n , y n ) , k 2 = h f ( x n + 1 2 h , y n + 1 2 k 1 ) , k 3 = h f ( x n + h , y n − k 1 + 2 k 2 ) . (10) \begin{aligned}&y_{n+1}=y_{n}+\frac{1}{6}(k_{1}+4k_{2}+k_{3}),\\&k_{1}=hf(x_{n}, y_{n}),\\&k_{2}=hf\left(x_{n}+\frac{1}{2}h,y_{n}+\frac{1}{2}k_{1}\right),\\&k_{3}=hf(x_{n}+h,y_{n}-k_{1}+2k_{2}).\end{aligned}\tag{10} yn+1=yn+61(k1+4k2+k3),k1=hf(xn,yn),k2=hf(xn+21h,yn+21k1),k3=hf(xn+h,yn−k1+2k2).(10)
4.1.3 三阶三段 Heun 公式
y n + 1 = y n + 1 4 ( k 1 + 3 k 3 ) , k 1 = h f ( x n , y n ) , k 2 = h f ( x n + 1 3 h , y n + 1 3 k 1 ) , k 3 = h f ( x n + 2 3 h , y n + 2 3 k 2 ) . (11) \begin{aligned}&y_{n+1}=y_{n}+\frac{1}{4}(k_{1}+3k_{3}),\\&k_{1}=hf(x_{n},y_{n}),\\&k_{2}=hf\left(x_{n}+\frac{1}{3}h,y_{n}+\frac{1}{3}k_{1}\right),\\&k_{3}=hf\left(x_{n}+\frac{2}{3}h,y_{n}+\frac{2}{3}k_{2}\right).\end{aligned}\tag{11} yn+1=yn+41(k1+3k3),k1=hf(xn,yn),k2=hf(xn+31h,yn+31k1),k3=hf(xn+32h,yn+32k2).(11)
4.1.4 标准四阶四段龙格 – 库塔公式
y n + 1 = y n + 1 6 ( k 1 + 2 k 2 + 2 k 3 + k 4 ) , k 1 = h f ( x n , y n ) , k 2 = h f ( x n + 1 2 h , y n + 1 2 k 1 ) , k 3 = h f ( x n + 1 2 h , y n + 1 2 k 2 ) , k 4 = h f ( x n + h , y n + k 3 ) . (12) \begin{aligned} y_{n+1}=& y_{n}+\frac{1}{6}(k_{1}+2k_{2}+2k_{3}+k_{4}), \\ k_{1}=& hf(x_{n},y_{n}), \\ k_{2}=& hf\left(x_{n}+\frac{1}{2}h,y_{n}+\frac{1}{2}k_{1}\right), \\ k_{3}=& hf\left(x_{n}+\frac{1}{2}h,y_{n}+\frac{1}{2}k_{2}\right), \\ k_{4}=& hf(x_{n}+h,y_{n}+k_{3}). \end{aligned}\tag{12} yn+1=k1=k2=k3=k4=yn+61(k1+2k2+2k3+k4),hf(xn,yn),hf(xn+21h,yn+21k1),hf(xn+21h,yn+21k2),hf(xn+h,yn+k3).(12)
在实际应用中 , 最常用的是标准四阶四段龙格 – 库塔公式 .
4.1.5 四阶四段 Gill 公式
y n + 1 = y n + 1 6 ( k 1 + ( 2 − 2 ) k 2 + ( 2 + 2 ) k 3 + k 4 ) , k 1 = h f ( x n , y n ) , k 2 = h f ( x n + 1 2 h , y n + 1 2 k 1 ) , k 3 = h f ( x n + 1 2 h , y n + 2 − 1 2 k 1 + 2 − 2 2 k 2 ) , k 4 = h f ( x n + h , y n − 2 2 k 2 + 2 + 2 2 k 3 ) . (13) \begin{aligned} y_{n+1}=& y_{n}+\frac{1}{6}(k_{1}+(2-\sqrt{2})k_{2}+(2+\sqrt{2})k_{3}+k_{4}), \\ k_{1}=& hf(x_{n},y_{n}), \\ k_{2}=& hf\left(x_{n}+\frac{1}{2}h,y_{n}+\frac{1}{2}k_{1}\right), \\ k_{3}=& hf\left(x_{n}+\frac{1}{2}h,y_{n}+\frac{\sqrt{2}-1}{2}k_{1}+\frac{2-\sqrt{2}}{2}k_{2}\right), \\ k_{4}=& hf\left(x_{n}+h,y_{n}-\frac{\sqrt{2}}{2}k_{2}+\frac{2+\sqrt{2}}{2}k_{3}\right). \end{aligned}\tag{13} yn+1=k1=k2=k3=k4=yn+61(k1+(2−2)k2+(2+2)k3+k4),hf(xn,yn),hf(xn+21h,yn+21k1),hf(xn+21h,yn+22−1k1+22−2k2),hf(xn+h,yn−22k2+22+2k3).(13)
RK方法的阶数与计算函数值的次数之间的关系并非等量增加的 ,事实上 , 对于大量的实际问题 , 四阶的龙格 – 库塔公式已可满足对精度的要求 :


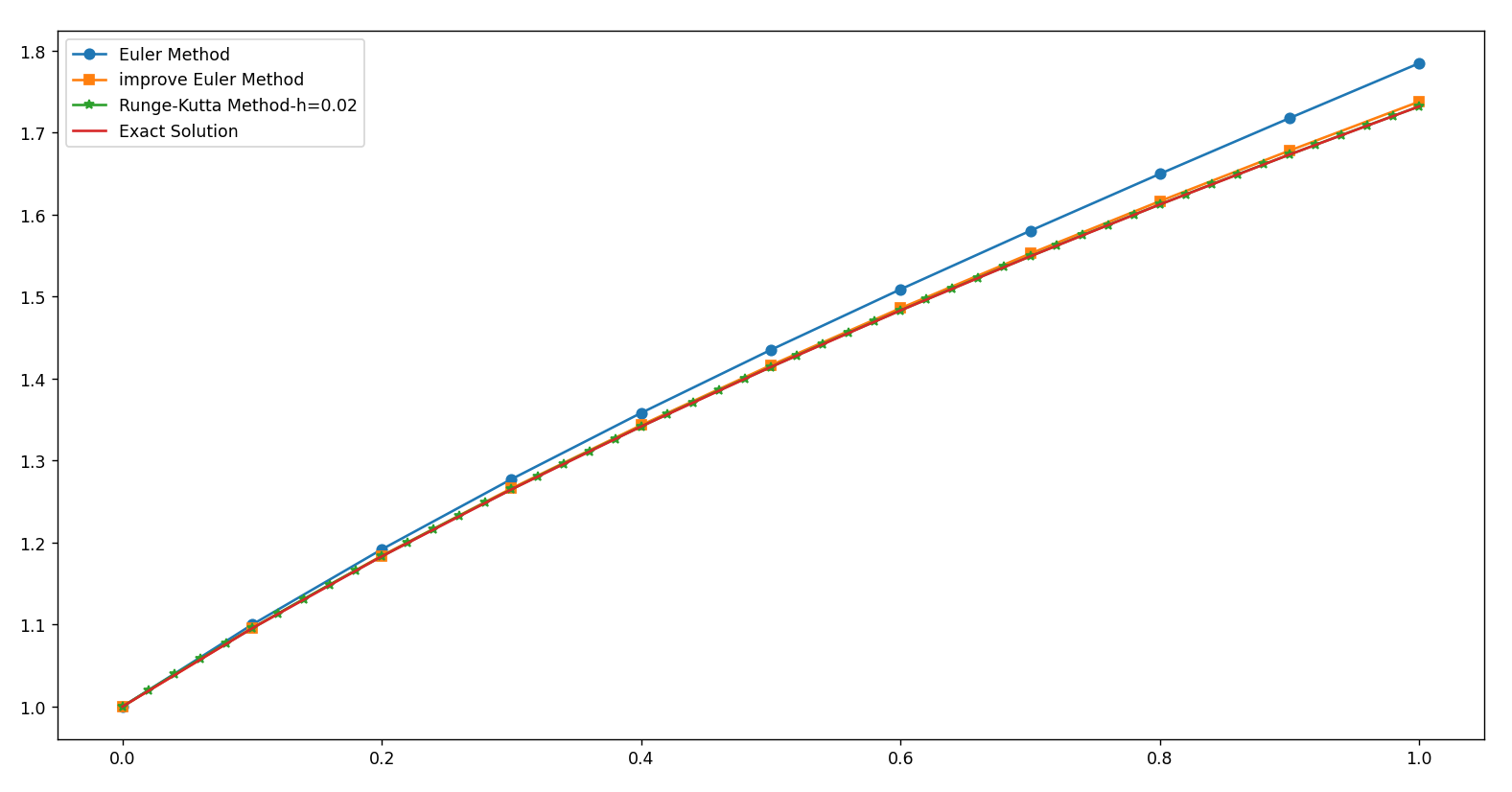
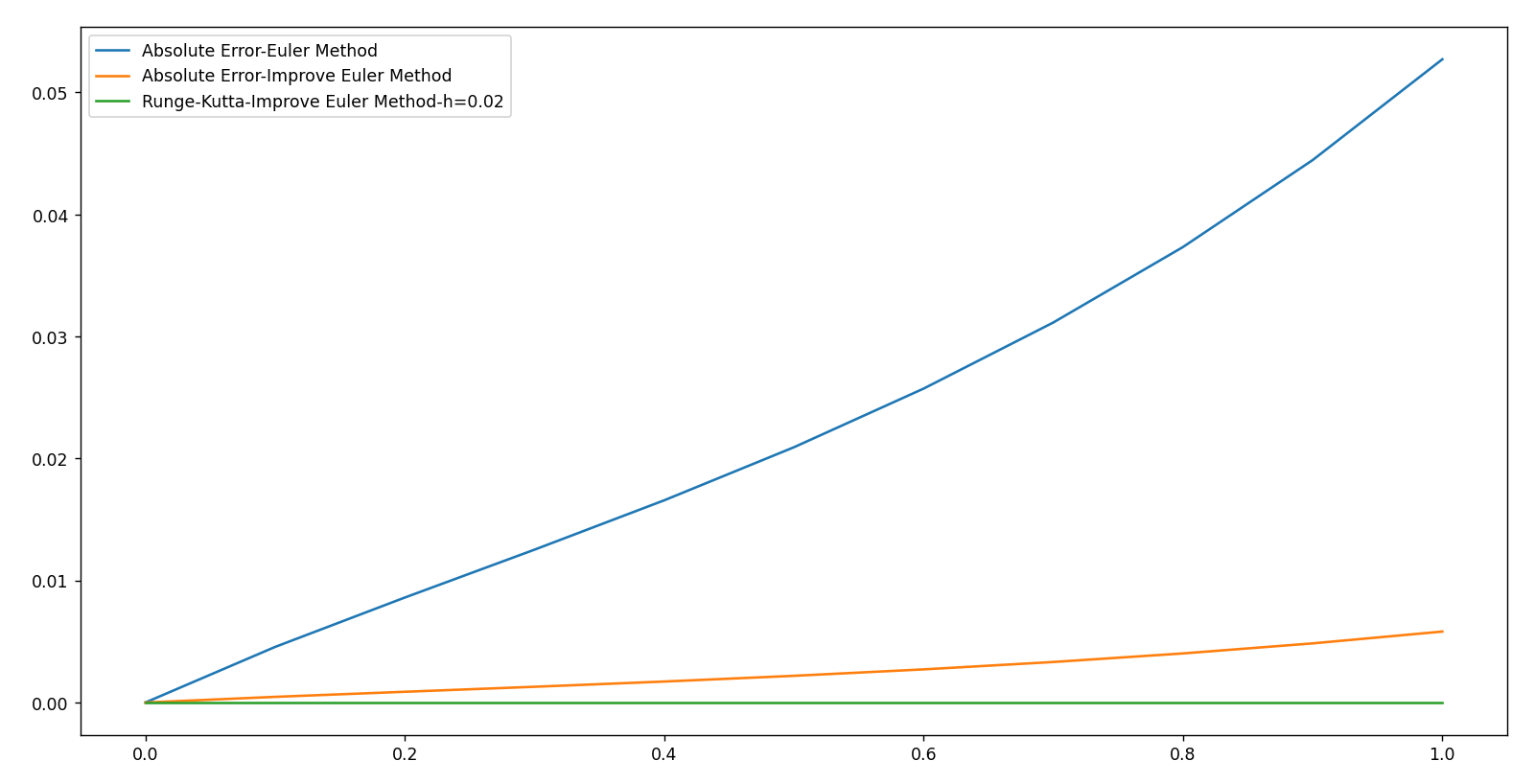
- RK44计算例题9.1.2
4.2龙格 – 库塔公式的优缺点
- 在求解范围较大而精度要求较高时是比较好的方法
- 显示格式且自启动.
- R-K公式基于泰勒展开,因此要求解函数y(x)具有较好的光滑性质
- 如果解y(x)光滑性差 , 那么四阶龙格 – 库塔公式求得的数值解精度可能反而不如改进的欧拉公式
5. 收敛性与稳定性
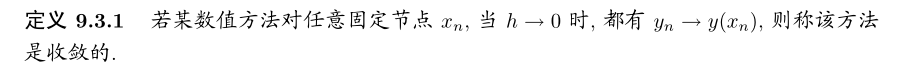


6. 微分方程组和刚性问题
本节讨论常微分方程组的数值解法
6.1 一阶常微分方程组
前面在未知函数个数 m = 1情况下得到的大部分结论都可平行地推广到 m > 1 的情况 ;前文介绍的梯形公式、预估校正格式和龙格 – 库塔公式均可应用于一阶常微分
方程组的求解 . 只是在进行理论分析时 , 需要将绝对值替换为向量范数
例如,考虑以下方程组:
( u ′ v ′ ) = ( 0 1 − x 2 − x ) ( u v ) + ( 0 x + 1 ) , x ∈ ( 0 , 10 ) , \left.\left(\begin{array}{c}u'\\v'\end{array}\right.\right)=\left(\begin{array}{cc}0&1\\-x^2&-x\end{array}\right)\left(\begin{array}{c}u\\v\end{array}\right)+\left(\begin{array}{c}0\\x+1\end{array}\right),\quad x\in(0,10), (u′v′)=(0−x21−x)(uv)+(0x+1),x∈(0,10),
( u ( 0 ) v ( 0 ) ) = ( a b ) . \left.\left(\begin{array}{c}u(0)\\\\v(0)\end{array}\right.\right)=\left(\begin{array}{c}a\\b\end{array}\right). u(0)v(0) =(ab).
将区间 [0,10] 进行 N 等分 , 记 h = 10 / N h =10/N h=10/N.将欧拉公式 (1.1) 应用于该问题 , 则有:
( u n + 1 v n + 1 ) = ( u n v n ) + h ( ( 0 1 − x n 2 − x n ) ( u n v n ) + ( 0 x n + 1 ) ) \left.\left(\begin{array}{c}u_{n+1}\\v_{n+1}\end{array}\right.\right)=\left(\begin{array}{c}u_{n}\\v_{n}\end{array}\right)+h\left(\left(\begin{array}{cc}0&1\\-x_{n}^{2}&-x_{n}\end{array}\right)\left(\begin{array}{c}u_{n}\\v_{n}\end{array}\right)+\left(\begin{array}{c}0\\x_{n}+1\end{array}\right)\right) (un+1vn+1)=(unvn)+h((0−xn21−xn)(unvn)+(0xn+1))
( u 0 v 0 ) = ( a b ) . \left.\left(\begin{array}{c}u_0\\v_0\end{array}\right.\right)=\left(\begin{array}{c}a\\b\end{array}\right). (u0v0)=(ab).
判断欧拉方法求解的绝对稳定性.可知方程组扰动表达式为:
( δ u n + 1 δ v n + 1 ) = ( 0 1 − x 2 − x ) ( δ u n δ v n ) , \left.\left(\begin{array}{c}\delta_u^{n+1}\\\delta_v^{n+1}\end{array}\right.\right)=\left(\begin{array}{cc}0&1\\-x^2&-x\end{array}\right)\left(\begin{array}{c}\delta_u^n\\\delta_v^n\end{array}\right), (δun+1δvn+1)=(0−x21−x)(δunδvn),
矩阵 ( 0 1 − x 2 − x ) \left(\begin{array}{cc}0&1\\-x^2&-x\end{array}\right) (0−x21−x)的特征值为 λ 1 , 2 = e ± 2 π 3 i x \lambda_{1,2}=\mathrm e^{\pm\frac{2\pi}{3}\mathrm i}x λ1,2=e±32πix. 可以证明当 ∣ h λ i ∣ < 1 ( 或 h < 0.1 ) |h\lambda_i|<1(\text{或 }h<0.1) ∣hλi∣<1(或 h<0.1)时,有:
∥ ( δ u n + 1 δ v n + 1 ) ∥ ⩽ ∥ ( δ u n δ v n ) ∥ , \left.\left\|\left(\begin{array}{c}\delta_u^{n+1}\\\delta_v^{n+1}\end{array}\right.\right)\right\|\leqslant\left\|\left(\begin{array}{c}\delta_u^n\\\delta_v^n\end{array}\right)\right\|, (δun+1δvn+1) ⩽ (δunδvn) ,
即该方法是绝对稳定的
6.2 高阶常微分方程初值问题
{ y ( n ) = f ( x , y ( x ) , y ′ ( x ) , ⋯ , y ( n − 1 ) ( x ) ) , x ∈ [ a , b ] , y ( a ) = y ~ 0 , y ′ ( a ) = y ~ 0 ′ , ⋯ , y ( n − 1 ) ( a ) = y ~ 0 ( n − 1 ) , (14) \left\{\begin{matrix}\begin{aligned}&y^{(n)}=f(x,y(x),y'(x),\cdots,y^{(n-1)}(x)),\quad x\in[a,b],\\&y(a)=\tilde{y}_{0}, y'(a)=\tilde{y}_{0}^{\prime},\cdots, y^{(n-1)}(a)=\tilde{y}_{0}^{(n-1)},\end{aligned}\end{matrix}\right.\tag{14} {y(n)=f(x,y(x),y′(x),⋯,y(n−1)(x)),x∈[a,b],y(a)=y~0,y′(a)=y~0′,⋯,y(n−1)(a)=y~0(n−1),(14)
记:
u = ( y ( x ) , y ′ ( x ) , ⋯ , y ( n − 1 ) ) T , y 0 = ( y ~ 0 , y ~ 0 ′ , ⋯ , y ~ 0 ( n − 1 ) ) T , \boldsymbol{u}=(y(x),y'(x),\cdots,y^{(n-1)})^\mathrm{T},\quad\boldsymbol{y_0}=(\tilde{y}_0,\tilde{y}_0',\cdots,\tilde{y}_0^{(n-1)})^\mathrm{T}, u=(y(x),y′(x),⋯,y(n−1))T,y0=(y~0,y~0′,⋯,y~0(n−1))T,
则可将高阶微分方程化为一阶微分方程组:
{ u ′ = f ( x , u ) u ( 0 ) = y 0 \left\{\begin{matrix}\boldsymbol{u}'=f(x,\boldsymbol{u}) \\\boldsymbol{u}(0)=y_0 \end{matrix}\right. {u′=f(x,u)u(0)=y0
例如,考虑初值问题:
{ y ′ ′ = − x y ′ − x 2 y + x + 1 , x ∈ [ 0 , 10 ] , y ( 0 ) = a , y ′ ( 0 ) = b . \left.\left\{\begin{array}{ll}y''=-xy'-x^2y+x+1,\quad x\in[0,10],\\y(0)=a,\quad y'(0)=b.\end{array}\right.\right. {y′′=−xy′−x2y+x+1,x∈[0,10],y(0)=a,y′(0)=b.
令 y = u , y ′ = v , y=u,y^{\prime}=v, y=u,y′=v,该初值问题转化成一阶常微分方程组:
( u ′ v ′ ) = ( 0 1 − x 2 − x ) ( u v ) + ( x + 1 0 ) \begin{pmatrix}u'\\v'\\\end{pmatrix}=\begin{pmatrix}0 &1\\-x^2 &-x\\\end{pmatrix}\begin{pmatrix}u\\v\\\end{pmatrix}+\begin{pmatrix}x+1\\0\\\end{pmatrix} (u′v′)=(0−x21−x)(uv)+(x+10)
( u 0 v 0 ) = ( a b ) \begin{pmatrix}u_0\\v_0\\\end{pmatrix}=\begin{pmatrix}a\\b\\\end{pmatrix} (u0v0)=(ab)
6.3 刚性方程组

例如 , 考虑常微分方程组
( u ′ v ′ ) = ( 9 24 − 24 − 51 ) ( u v ) + ( 5 cos x − 1 3 sin x − 9 cos x + 1 3 sin x ) , x ∈ ( 0 , 1 ) , \left(\begin{array}{c}u'\\v'\end{array}\right)=\left(\begin{array}{cc}9&24\\-24&-51\end{array}\right)\left(\begin{array}{c}u\\v\end{array}\right)+\left(\begin{array}{c}5\cos x-\frac{1}{3}\sin x\\\\-9\cos x+\frac{1}{3}\sin x\end{array}\right),\quad x\in(0,1), (u′v′)=(9−2424−51)(uv)+ 5cosx−31sinx−9cosx+31sinx ,x∈(0,1),
( u ( 0 ) v ( 0 ) ) = ( 4 3 2 3 ) . \left.\left(\begin{array}{c}u(0)\\v(0)\end{array}\right.\right)=\left(\begin{array}{c}\frac{4}{3}\\\frac{2}{3}\end{array}\right). (u(0)v(0))=(3432).
这就是一个刚性方程组 , 其雅可比矩阵为 ( 9 24 − 24 − 51 ) , \left(\begin{array}{cc}9&24\\-24&-51\end{array}\right), (9−2424−51),刚性比 s = ∣ − 39 ∣ ∣ − 3 ∣ = 13 s={\frac{|-39|}{|-3|}}=13 s=∣−3∣∣−39∣=13,存在唯一解:
u = 2 e − 3 x − e − 39 x + 1 3 cos x , v = − e − 3 x + 2 e − 39 x − 1 3 cos x . u=2\mathrm{e}^{-3x}-\mathrm{e}^{-39x}+\frac13\cos x,\quad v=-\mathrm{e}^{-3x}+2\mathrm{e}^{-39x}-\frac13\cos x. u=2e−3x−e−39x+31cosx,v=−e−3x+2e−39x−31cosx.
求解刚性问题的困难之处:为保证算法的稳定性 , 必须将步长限制在较小的范围内.若需要计算到某一个较长的区间 , 则需要迭代非常多的时间步 . 这导致计算量大 , 并且由于舍入误差的累计 , 结果也很不准确
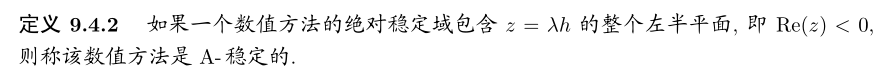
对于刚性问题 , 如果扩大数值方法的绝对稳定区域,步长的限制讲大大减少.若某数值方法是 A- 稳定的 , 则应用该方法时步长可随意选取 , 不再受稳定性限制
显式多步法和显式龙格 – 库塔法不可能是 A- 稳定的 , A- 稳定的隐式线性多步法的阶不超过 2, 而梯形公式是二阶隐式线性多步法中精度最高的一个
实际计算时 , 常采用隐式或半隐式的龙格 – 库塔公式求解刚性方程组
以下是 A- 稳定的的常用计算格式:
一段二阶隐式龙格 – 库塔方法
{ y n + 1 = y n + h k 1 , k 1 = f ( x n + h 2 , y n + h 2 k 1 ) . \begin{cases}&y_{n+1}=y_n+hk_1,\\&k_1=f\left(x_n+\frac{h}{2},y_n+\frac{h}{2}k_1\right).\end{cases} {yn+1=yn+hk1,k1=f(xn+2h,yn+2hk1).
二段二阶隐式龙格 – 库塔方法
{ y n + 1 = y n + h 2 ( k 1 + k 2 ) , k 1 = f ( x n , y n ) , k 2 = f ( x n + h , y n + h 2 ( k 1 + k 2 ) ) . \begin{cases}&y_{n+1}=y_{n}+\frac{h}{2}(k_{1}+k_{2}),\\&k_{1}=f(x_{n},y_{n}),\\&k_{2}=f\left(x_{n}+h,y_{n}+\frac{h}{2}(k_{1}+k_{2})\right).\end{cases} ⎩ ⎨ ⎧yn+1=yn+2h(k1+k2),k1=f(xn,yn),k2=f(xn+h,yn+2h(k1+k2)).
二段四阶隐式龙格 – 库塔方法
y n + 1 = y n + h 2 ( k 1 + k 2 ) , k 1 = f ( x n + ( 1 2 + 3 6 ) h , y n + h 4 ( k 1 + ( 1 + 2 3 3 k 2 ) ) , 2 = f ( x n + ( 1 2 − 3 6 ) h , y n + h 4 ( ( 1 − 2 3 3 ) k 1 + k 2 ) ) . \begin{aligned}&y_{n+1}=y_{n}+\frac{h}{2}(k_{1}+k_{2}),\\&k_{1}=f \left(x_{n} + \left(\frac{1}{2} + \frac{\sqrt{3}}{6}\right) h,y_{n} + \frac{h}{4} \left(k_{1} + \left(1 + \frac{2\sqrt{3}}{3}k_{2}\right)\right),\\_{2}=f \left(x_{n} + \left(\frac{1}{2} - \frac{\sqrt{3}}{6}\right)h,y_{n} + \frac{h}{4} \left(\left(1-\frac{2\sqrt{3}}{3}\right)k_{1} + k_{2}\right)\right) .\right.\end{aligned} yn+1=yn+2h(k1+k2),k1=f(xn+(21+63)h,yn+4h(k1+(1+323k2)),2=f(xn+(21−63)h,yn+4h((1−323)k1+k2)).
半隐式龙格 – 库塔方法
y n + 1 = y n + k 2 , y_{n+1}=y_n+k_2, yn+1=yn+k2,
k 1 = f ( x n , y n ) + ( 1 − 2 2 ) h 2 ∂ f ∂ x ( x n , y n ) + ( 1 − 2 2 ) h ∂ f ∂ y ( x n , y n ) k 1 , k_1=f(x_n,y_n)+\left(1-\frac{\sqrt{2}}{2}\right)h^2\frac{\partial f}{\partial x}(x_n,y_n)+\left(1-\frac{\sqrt{2}}{2}\right)h\frac{\partial f}{\partial y}(x_n,y_n)k_1, k1=f(xn,yn)+(1−22)h2∂x∂f(xn,yn)+(1−22)h∂y∂f(xn,yn)k1,
k 2 = h f ( x n + 2 − 1 2 h , y n + 2 − 1 2 k 1 ) + ( 1 − 2 2 ) h 2 ∂ f ∂ x ( x n , y n ) + ( 1 − 2 2 ) h ∂ f ∂ y ( x n , y n ) k 2 . \begin{aligned}k_{2}&=hf\left(x_{n}+\frac{\sqrt{2}-1}{2}h,y_{n}+\frac{\sqrt{2}-1}{2}k_{1}\right)+\left(1-\frac{\sqrt{2}}{2}\right)h^{2}\frac{\partial f}{\partial x}(x_{n},y_{n})\\&+\left(1-\frac{\sqrt{2}}{2}\right)h\frac{\partial f}{\partial y}(x_{n},y_{n})k_{2}.\end{aligned} k2=hf(xn+22−1h,yn+22−1k1)+(1−22)h2∂x∂f(xn,yn)+(1−22)h∂y∂f(xn,yn)k2.
7. 有限差分法
简单介绍该方法的基本思想
有限差分法离散微分方程包含两步:
- 第一步是将求解区域进行网格剖分 ;
- 第二步是将微分方程在节点处进行离散化 .
建立差分格式的离散化方法有多种 , 这里仅介绍以差商代替微商的方法
以第二类常微分问题(两阶常微分方程边值问题为例子):
{ − y ′ ′ + q ( x ) y = f ( x ) , x ∈ [ a , b ] , y ( a ) = α , y ( b ) = β , (16) \left.\left\{\begin{array}{c}-y''+q(x)y=f(x),\quad x\in[a,b],\\y(a)=\alpha, y(b)=\beta,\end{array}\right.\right.\tag{16} {−y′′+q(x)y=f(x),x∈[a,b],y(a)=α,y(b)=β,(16)
对于内部节点 x n ( n = 1 , 2 , ⋅ ⋅ ⋅ , N − 1 ) x_n (n = 1,2,··· ,N − 1) xn(n=1,2,⋅⋅⋅,N−1), 由泰勒展开公式得
y ( x n + 1 ) − 2 y ( x n ) + y ( x n − 1 ) h 2 = [ d 2 y d x 2 ] n + h 2 12 [ d 4 y d x 4 ] n + O ( h 3 ) . \frac{y(x_{n+1})-2y(x_n)+y(x_{n-1})}{h^2}=\left[\frac{\mathrm{d}^2y}{\mathrm{d}x^2}\right]_n+\frac{h^2}{12}\left[\frac{\mathrm{d}^4y}{\mathrm{d}x^4}\right]_n+O(h^3). h2y(xn+1)−2y(xn)+y(xn−1)=[dx2d2y]n+12h2[dx4d4y]n+O(h3).
[ ] n [ ]_n []n 表示方括号内的函数在点 x n x_n xn 取值,所以方程(16)在 x n x_n xn写成:
− y ( x n + 1 ) − 2 y ( x n ) + y ( x n − 1 ) h 2 + q ( x n ) y ( x n ) = f ( x n ) + R n ( y ) , R n ( y ) = − h 2 12 [ d 4 y d x 4 ] n + O ( h 3 ) . -\frac{y(x_{n+1})-2y(x_{n})+y(x_{n-1})}{h^{2}}+q(x_{n})y(x_{n})=f(x_{n})+R_{n}(y),\\R_{n}(y)=-\frac{h^{2}}{12}\left[\frac{\mathrm{d}^{4}y}{\mathrm{d}x^{4}}\right]_{n}+O(h^{3}). −h2y(xn+1)−2y(xn)+y(xn−1)+q(xn)y(xn)=f(xn)+Rn(y),Rn(y)=−12h2[dx4d4y]n+O(h3).
h 充分小时 , R n ( y ) R_n (y) Rn(y) 是的二阶无穷小量,因此差分方程为, R n ( y ) R_n (y) Rn(y) 为截断误差:
{ − y n + 1 − 2 y n + y n − 1 h 2 + q n y n = f n , q n = q ( x n ) , f n = f ( x n ) . \left\{\begin{matrix} -\frac{y_{n+1}-2y_n+y_{n-1}}{h^2}+q_ny_n=f_n,\\q_n=q(x_n), f_n=f(x_n).\\\end{matrix}\right. {−h2yn+1−2yn+yn−1+qnyn=fn,qn=q(xn),fn=f(xn).
对于边界节点 , 由边界条件知 y 0 = α , y N = β . y_{0}=\alpha, y_{N}=\beta. y0=α,yN=β.
可得到关于 y_n 的线性代数方程组:
{ − y n + 1 − 2 y n + y n − 1 h 2 + q n y n = f n , n = 1 , ⋯ , N − 1 y 0 = α , y N = β . \left\{\begin{array}{ll}-\frac{y_{n+1}-2y_n+y_{n-1}}{h^2}+q_ny_n=f_n,\quad n=1,\cdots,N-1\\\\y_0=\alpha,\quad y_N=\beta.\end{array}\right. ⎩ ⎨ ⎧−h2yn+1−2yn+yn−1+qnyn=fn,n=1,⋯,N−1y0=α,yN=β.
记方程组的未知向量 y h = ( y 1 , y 2 , ⋯ , y N − 1 ) T , y_h = (y_1,y_2,\cdots,y_{N-1})^\mathrm{T}, yh=(y1,y2,⋯,yN−1)T, 右端向量为 g = ( f 1 + α h 2 , f 2 , ⋯ , f N − 1 + β h 2 ) g = \left(f_{1} + \frac{\alpha}{h^{2}},f_{2},\cdots,f_{N-1} +\frac{\beta}{h^2}\right) g=(f1+h2α,f2,⋯,fN−1+h2β),系数矩阵为:
H = ( 2 h 2 + q 1 − 1 h 2 0 ⋯ 0 − 1 h 2 2 h 2 + q 2 − 1 h 2 ⋯ 0 0 − 1 h 2 2 h 2 + q 3 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ 2 h 2 + q N − 1 ) , \left.\boldsymbol{H}=\left(\begin{array}{ccccc}\frac{2}{h^{2}}+q_{1}&-\frac{1}{h^{2}}&0&\cdots&0\\\\-\frac{1}{h^{2}}&\frac{2}{h^{2}}+q_{2}&-\frac{1}{h^{2}}&\cdots&0\\\\0&-\frac{1}{h^{2}}&\frac{2}{h^{2}}+q_{3}&\cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&\frac{2}{h^{2}}+q_{N-1}\end{array}\right.\right), H= h22+q1−h210⋮0−h21h22+q2−h21⋮00−h21h22+q3⋮0⋯⋯⋯⋱⋯000⋮h22+qN−1 ,
则有:
H y h = g . Hy_{h}=g. Hyh=g.
易知 , H 为对称正定矩阵 , 故该方程组有唯一解 . 此外 , 由于矩阵 H 为三对角阵