题意
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
1 <= num1.length, num2.length <= 200
难度
中等
示例
输入: num1 = "2", num2 = "3"
输出: "6"
输入: num1 = "123", num2 = "456"
输出: "56088"分析
来回忆一下小学阶段,我们是怎么做乘法运算的:
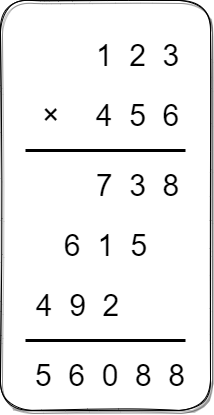
列竖式,计算每一位的乘积,然后错位相加。这也是我们解决这道题的 “灵丹妙药”。
假如输入是 123 * 456,我们来看一下:
7 3 8的 第0位——8 是由123的 第0位——3 和456的 第0位——6 相乘并向第 1 位进 1 后得到的;7 3 8的 第1位——3 是由123的 第1位——2 和456的 第0位——6 相乘,再加上一次的进位1,并向第 2 位进 1 得到的;7 3 8的 第2位——7 是由123的 第2位——1 和456的 第0位——6 相乘,再加上一次的进位1得到的(不需要再进位);6 1 5的 第1位——5 是由123的 第0位——3 和456的 第1位——5 相乘并进位得到的;6 1 5的 第2位——1 是由123的 第1位——2 和456的 第1位——5 相乘并进位得到的;- ...
有没有看出来一点端倪?
两个乘数的长度分别是 m 和 n,那么乘积的长度最多是 m + n。
两个乘数的第 i 位和第 j 位相乘的结果会出现在乘积的第 i + j 位。
我们可以用一个数组来存储每一位的乘积,然后再将数组中的每一位错位相加,最后得到结果。
当输入是 123 * 456 的时候,我们来简单模拟一下前三个步骤:
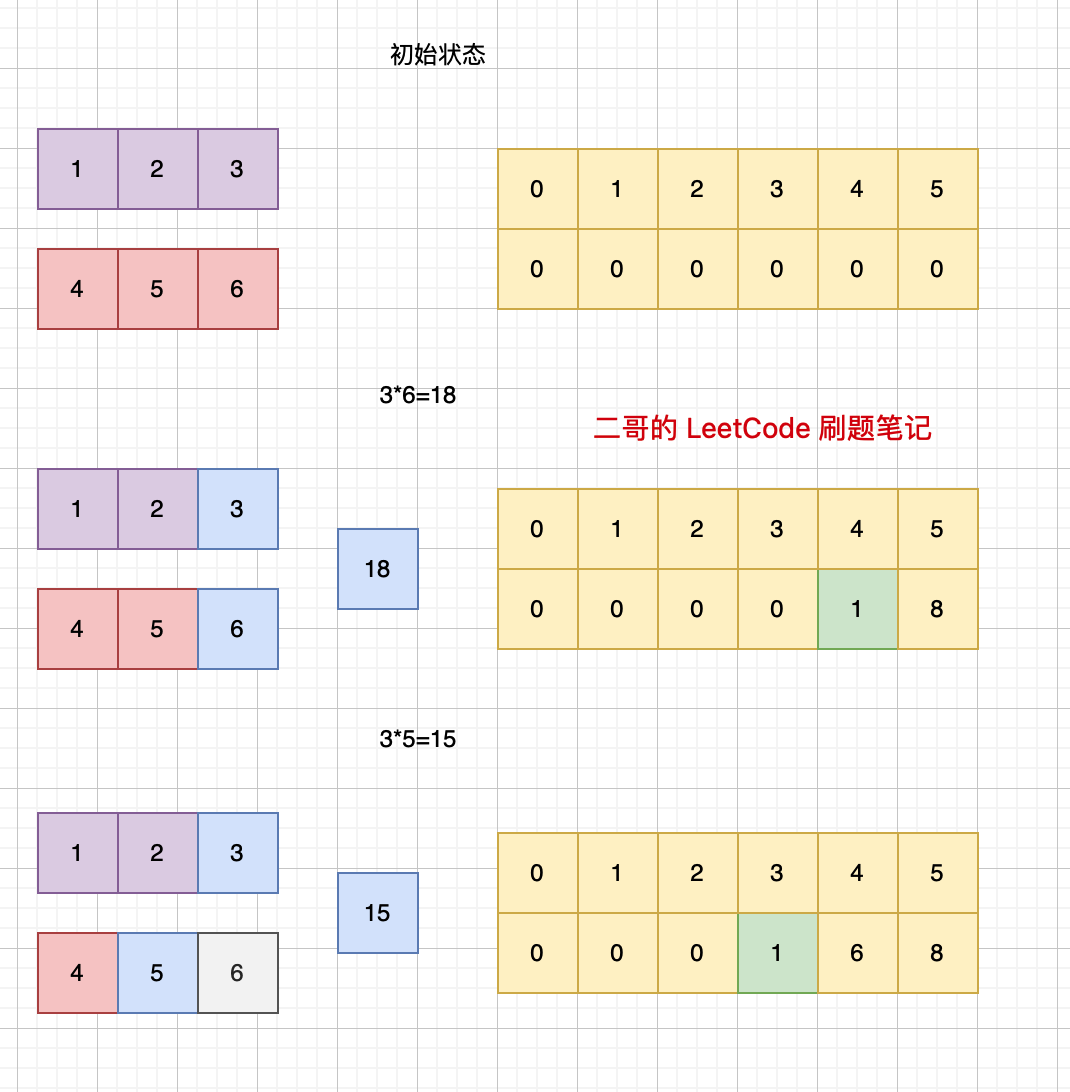
初始状态的时候,我们可以看到,result 数组的长度是 m + n,每一位都是 0。
第一步,我们计算 3 * 6,得到 18,然后将 8 存储在 result[5],1 进位存储在 result[4]。
第二步,我们计算 3 * 5,得到 15,加上之前进位的 1 是 16,然后将 6 存储在 result[4],1 进位存储在 result[3]。
依次类推,我们可以得到最终的结果 56088。来看题解代码:
/**
* @ClAssName StringMultiply
* @Description 字符串相乘,给定数字字符串,返回两个数字的乘积
* @Author 欧妮甲是神仙
* @Date 2024/8/9 21:{MINUTE}
*/
public class StringMultiply {
public static void main(String[] args) {
String multiply = new StringMultiply().multiply("123", "456");
System.out.println("两数的沉积为:" + multiply);
System.out.println("%%%%%%%%%%%%%%%%%");
String s1 = "123";
String s2 = "456";
int i = Integer.parseInt(s1);
int i1 = Integer.parseInt(s2);
System.out.println("两数的乘积为:" + i * i1);
System.out.println("**************************");
String num1 = new StringMultiply().multiply1("123", "456");
System.out.println("两数的沉积为:" + num1);
}
public String multiply1(String num1, String num2)
{
BigInteger n1 = new BigInteger(num1);
BigInteger n2 = new BigInteger(num2);
return n1.multiply(n2).toString();
}
public String multiply(String num1, String num2) {
//定义一个数组,用于存储结果
int[] res = new int[num1.length() + num2.length()];
//遍历两个字符串,将字符串的每一位取出来相乘,从右到左依次相乘
for (int i= num1.length()-1; i >=0 ; i--) {
for (int j = num2.length()-1; j >=0 ; j--) {
//取出每一位将其·转化为数字并相乘
int n1 = (num1.charAt(i) - '0') * (num2.charAt(j) - '0');
//将得到的乘积拆分,分别存储到对应位置
int p1 = i+j+1;
int p2 = i+j;
//将乘积的每一位放到相应的位置
int sum = n1 + res[p1];
res[p1] = sum%10; //个位
res[p2] += sum/10; //进位。十位数
}
}
// 将结果数组转换为字符串
StringBuilder builder = new StringBuilder();
for (int i = 0; i < res.length; i++) {
if (!(builder.length() == 0 && res[i] == 0)){//去掉前导0
builder.append(res[i]);
}
}
return builder.length() == 0? "0" : builder.toString();//处理为0的情况
}
}
- 双重循环遍历 num1 和 num2 的每一位,计算乘积 mul。
int p1 = i + j + 1,p2 = i + j:确定乘积在结果数组中的位置。int sum = mul + res[p1]:当前乘积加上当前位置已有的值(注意进位)。result[p1] = sum % 10:存储当前位。result[p2] += sum / 10:处理进位。
这里有三个小技巧:
- 我们可以从字符串的最后一位开始遍历,这样就省去了反转字符串的操作。
- 最后注意要去掉结果数组中的前导零,因为最后一次计算不需要进位的话,会在结果数组的最高位存储 0。
char - '0'可以将字符转换为数字,这个知识点之前应该也讲过。
好,我们来看一下在Leetcode上面跑的效率。
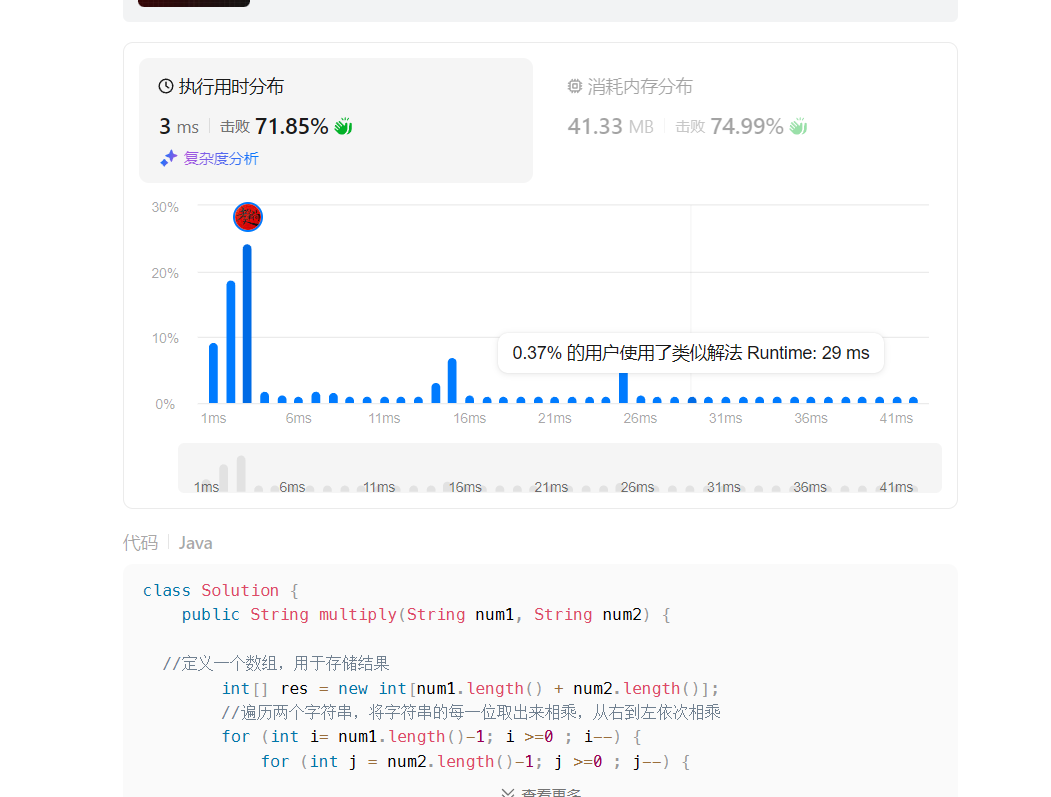
总结
讲真心话,我对这种题目不是很感冒,觉得已有乘法运算的话,直接调用就好了呀。😄
但是有时候,算法考察的就是我们的思维能力,或者叫造轮子能力,一道乘法运算的题目,最终考察的还是我们对数组、for 循环和进位的理解。
以及一些细节处理,比如说去掉前导零。99*99 的结果是 9801,不用考虑 0 的问题;但 11*11 的结果是 121,按照我们的题解方法数组的千位就是 0,所以我们要去掉。
力扣链接:. - 力扣(LeetCode)

![[io]进程间通信 -信号函数 —信号处理过程](https://i-blog.csdnimg.cn/direct/e1829f8ce9314f39a01f76f7a9a3f557.png)













![[BSidesCF 2019]Kookie1](https://i-blog.csdnimg.cn/direct/0d7a0cb6275840c8878f4ee7a4e7266f.png)