🍃作者介绍：双非本科大三网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发、数据结构和算法，初步涉猎人工智能和前端开发。
🦅个人主页：@逐梦苍穹
📕所属专栏：人工智能
🌻gitee地址：xzl的人工智能代码仓库
✈ 您的一键三连，是我创作的最大动力🌹

1、简介

学习目标：

• 掌握RNN网络原理
• 掌握PyTorch RNN api

---

上一篇讲了词嵌入层，可以将文本数据映射为数值向量，进而能够送入到网络进行计算。

不清楚的可以复习一下：https://xzl-tech.blog.csdn.net/article/details/140942295

但是，还存在一个问题，文本数据是具有序列特性的，如果颠倒了顺序，那么可能就会表达不同的意思。
为了能够表示出数据的序列关系我们需要使用循环神经网络(Recurrent Nearal Networks, RNN) 来对数据进行建模，RNN 是一个 具有记忆功能的网络，它作用于处理带有序列特点的样本数据。
本文将会带着大家深入学习 RNN 循环网络层的原理、计算过程，以及在 PyTorch 中如何使用 RNN 层。

2、RNN 网络原理

当我们希望使用循环网络来对 “我爱你” 进行语义提取时，RNN 是如何计算过程是什么样的呢？

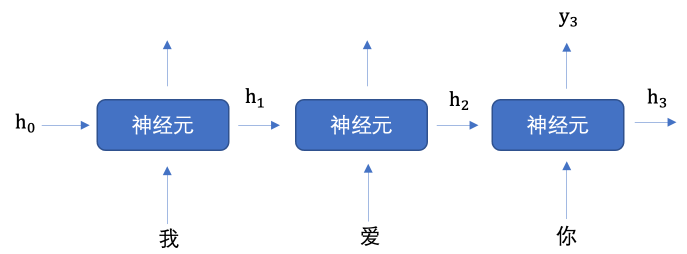
上图中 h 表示隐藏状态, 每一次的输入都会有包含两个值：上一个时间步的隐藏状态、当前状态的输入值，输出当前时间步的隐藏状态。
上图中，为了更加容易理解，虽然我画了 3 个神经元, 但是实际上只有一个神经元，

“我爱你” 三个字是重复输入到同一个神经元中。
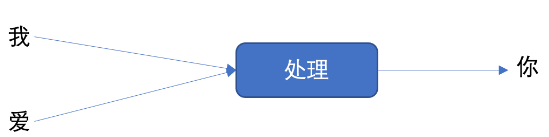
接下来，我们举个例子来理解上图的工作过程，假设我们要实现文本生成，也就是输入 “我爱” 这两个字，来预测出 “你”，其如下图所示:

我们将上图展开成不同时间步的形式，如下图所示:

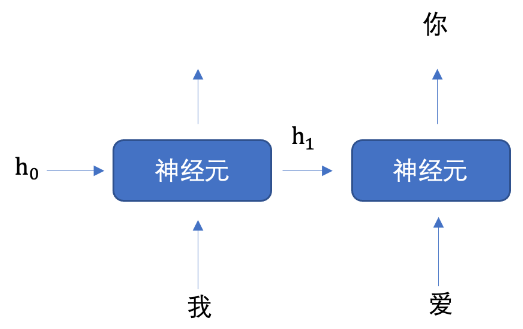
我们首先初始化出第一个隐藏状态，一般都是全0的一个向量，然后将 “我” 进行词嵌入，转换为向量的表示形式，送入到第一个时间步，然后输出隐藏状态 h1，
然后将 h1 和 “爱” 输入到第二个时间步，得到隐藏状态 h2,
将 h2 送入到全连接网络，得到 “你” 的预测概率。
那么，你可能会想，循环网络只能有一个神经元吗？
我们的循环网络网络可以有多个神经元，如下图所示：

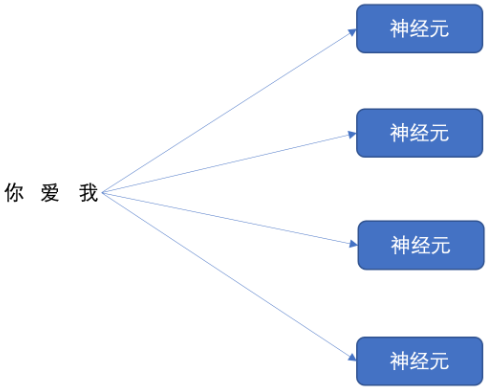
我们依次将 “我爱你” 三个字分别送入到每个神经元进行计算，
假设 词嵌入时，“我爱你” 的维度为 128，经过循环网络之后，“我爱你” 三个字的词向量维度就会变成 4
所以, 我们理解了循环神经网络的的神经元个数会影响到输出的数据维度。
每个神经元内部是如何计算的呢？
隐藏状态$h_t$的更新公式：$h_t=\tanh (W_{ih}{x}_t+b_{ih}+W_{hh}{h}_{(t-1)}+b_{hh})$
上述公式中：

1. $W_{ih}$ 表示输入数据的权重
2. $b_{ih}$ 表示输入数据的偏置
3. $W_{hh}$ 表示输入隐藏状态的权重
4. $b_{hh}$ 表示输入隐藏状态的偏置

最后对输出的结果使用 tanh 激活函数进行计算，得到该神经元 的输出。

3、PyTorch RNN 层的使用

接下来，我们学习 PyTorch 的 RNN 层的用法。
先牢记一下RNN的图：

注意：RNN 层输入的数据为三个维度：(seq_len, batch_size, input_size)【下文详解】
下面是代码的操作，首先先导包：

3.1、RNN送入单个数据

代码：

# 1. RNN 送入单个数据
def test01():  # 定义一个名为test01的函数，用于测试RNN输入单个数据样本
    # 输入数据维度 128, 输出维度 256
    rnn = nn.RNN(input_size=128, hidden_size=256)  # 创建一个RNN实例，指定输入特征维度为128，隐藏层维度为256

    # 第一个数字: 表示句子长度
    # 第二个数字: 批量个数
    # 第三个数字: 表示数据维度
    inputs = torch.randn(1, 1, 128)  # 生成一个形状为(1, 1, 128)的随机张量，表示单个时间步长、批量大小为1的数据输入
    print("inputs: ", inputs)
    print('-' * 82)
    hn = torch.zeros(1, 1, 256)  # 生成一个形状为(1, 1, 256)的零张量，初始化RNN的初始隐藏状态
    print("hn: ", hn)
    print('-' * 82)
    output, hn = rnn(inputs, hn)  # 将输入数据和隐藏状态传递给RNN，获取输出和更新后的隐藏状态
    print(output.shape)  # 打印输出张量的形状
    print(hn.shape)  # 打印更新后的隐藏状态张量的形状

输出：

E:\anaconda3\python.exe D:\Python\AI\神经网络\17-RNN.py 
inputs:  tensor([[[-0.0542,  1.3374,  0.6276,  1.6742, -1.6218,  1.4523, -0.5415,
           0.3223, -0.3032, -0.8091, -0.0138, -0.5916,  1.4253, -1.8918,
           1.2403, -1.2810,  0.3545, -0.8638,  0.1027, -0.2377,  1.1074,
           0.2798, -0.1968,  0.2442, -0.2380,  0.7400, -0.2120, -0.9833,
          -0.2811,  1.2074,  0.7339, -1.0456,  0.0399,  0.0785, -0.4130,
          -0.0441,  1.3400,  0.2237, -0.1764,  0.6922,  1.9262, -0.5288,
          -1.4500, -0.7859, -0.5073, -0.5422, -1.5230,  0.5099, -1.6504,
           0.1390,  1.6283, -0.4893, -2.3036,  1.0457, -0.2375, -0.9426,
           1.0307, -0.6329, -1.1034,  0.5635, -0.7559, -0.7063, -2.2348,
          -0.3007, -0.1424,  0.1728, -0.9499,  0.5152, -0.1789, -0.5752,
          -1.5950,  1.5423, -1.0990, -0.2535,  0.8160,  1.7046, -1.0907,
          -0.1915,  0.3198,  1.6223, -0.9377, -0.0530,  0.0468,  1.5816,
           0.2329,  1.0485,  1.2564, -0.7583,  1.1509,  0.1335,  0.2903,
          -0.8026,  0.1386,  1.0963,  0.0977, -0.1860,  1.6175,  0.7091,
          -0.7990,  0.3834, -0.9230,  0.2036, -0.3008,  1.2413,  0.1448,
          -0.0353,  1.7380, -0.3530, -0.7767,  0.6136, -0.6987,  0.4963,
          -1.3560, -1.8029, -1.2748, -0.3501,  0.5846, -1.4234, -0.7564,
           0.6593, -0.6481, -0.7269, -0.1935,  1.7772,  1.9999,  0.8682,
          -2.1852, -0.2099]]])
----------------------------------------------------------------------------------
hn:  tensor([[[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
          0., 0., 0.]]])
----------------------------------------------------------------------------------
torch.Size([1, 1, 256])
torch.Size([1, 1, 256])

Process finished with exit code 0

3.2、RNN层送入批量数据

代码：

# 2. RNN层送入批量数据
def test02():  # 定义一个名为test02的函数，用于测试RNN输入批量数据样本
    # 输入数据维度 128, 输出维度 256
    rnn = nn.RNN(input_size=128, hidden_size=256)  # 创建一个RNN实例，输入特征维度为128，隐藏层维度为256

    # 第一个数字: 表示句子长度
    # 第二个数字: 批量个数
    # 第三个数字: 表示数据维度
    # TODO 32批, 每批128
    inputs = torch.randn(1, 32, 128)  # 生成形状为(1, 32, 128)的随机张量，表示单个时间步长、批量大小为32的数据输入
    print("inputs.shape: ", inputs.shape)
    print("inputs: ", inputs)
    print('-' * 82)
    hn = torch.zeros(1, 32, 256)  # 生成形状为(1, 32, 256)的零张量，初始化RNN的初始隐藏状态
    print("hn.shape: ", hn.shape)
    print("hn: ", hn)
    print('-' * 82)

    output, hn = rnn(inputs, hn)  # 将批量输入数据和隐藏状态传递给RNN，获取输出和更新后的隐藏状态
    print(output.shape)  # 打印输出张量的形状
    print(hn.shape)  # 打印更新后的隐藏状态张量的形状

输出：

E:\anaconda3\python.exe D:\Python\AI\神经网络\17-RNN.py 
inputs.shape:  torch.Size([1, 32, 128])
inputs:  tensor([[[-0.3927, -1.7682,  0.7539,  ...,  0.7423,  0.6973, -1.1517],
         [-0.5867, -2.2071,  1.6128,  ..., -0.0758,  0.3444,  1.2695],
         [ 1.7433,  0.4850,  1.2588,  ..., -0.8928,  0.0400, -0.9688],
         ...,
         [-0.2075, -0.6588, -0.4446,  ...,  0.9307,  0.4107,  0.1857],
         [ 0.6601, -1.3952,  0.5381,  ...,  1.3603,  1.4538,  0.6282],
         [ 0.5128, -0.1883, -0.8761,  ..., -0.5208,  1.4437,  0.4713]]])
----------------------------------------------------------------------------------
hn.shape:  torch.Size([1, 32, 256])
hn:  tensor([[[0., 0., 0.,  ..., 0., 0., 0.],
         [0., 0., 0.,  ..., 0., 0., 0.],
         [0., 0., 0.,  ..., 0., 0., 0.],
         ...,
         [0., 0., 0.,  ..., 0., 0., 0.],
         [0., 0., 0.,  ..., 0., 0., 0.],
         [0., 0., 0.,  ..., 0., 0., 0.]]])
----------------------------------------------------------------------------------
torch.Size([1, 32, 256])
torch.Size([1, 32, 256])

Process finished with exit code 0

4、RNN三个维度

在使用循环神经网络（RNN）时，输入数据的维度通常是一个非常重要的考虑因素。RNN层期望的数据格式通常为三维张量 (seq_len, batch_size, input_size)。以下是对这三个维度的详细解释：

4.1、解释

1. seq_len（序列长度）：
   • 定义：seq_len 是每个输入序列中的时间步数，或者说每个输入序列包含的元素数量。
   • 例子：在文本处理中，seq_len 可能表示句子或文本的长度（例如，一个句子有多少个词）。在时间序列数据中，它表示时间步的数量（例如，股票价格的每日记录数）。
2. batch_size（批次大小）：
   • 定义：batch_size 是同时处理的序列数量。神经网络通常会批量处理数据，以提高计算效率。
   • 例子：如果您的数据集一次性处理10个序列，batch_size 就是10。这意味着网络会同时处理这10个序列的输入，进行并行计算。
3. input_size（输入大小）：
   • 定义：input_size 是每个时间步的输入特征数，表示每个输入向量的维度。
   • 例子：在文本处理中，input_size 通常是词嵌入的维度。例如，如果每个词用一个128维的向量表示，input_size 就是128。在多变量时间序列中，这可能是每个时间步的特征数量。

4.2、输入数据的组织

RNN层输入的数据组织方式使得网络可以有效处理批量数据和序列数据。具体来讲：

• 批处理：通过批处理多个序列，模型能够利用硬件的并行计算能力，提升训练和预测速度。
• 序列处理：通过在序列的每个时间步上操作，RNN可以捕捉到输入序列中的时间依赖性和顺序信息。

4.3、示例

假设有一个包含5个单词的句子，每个单词用300维的词向量表示，并且您一次处理20个句子。
则输入张量的维度为 (5, 20, 300)：

• seq_len = 5：表示每个句子有5个单词。
• batch_size = 20：表示同时处理20个句子。
• input_size = 300：表示每个单词的词向量是300维。

4.4、为什么需要这种格式？

• 时间序列特性：RNN的结构设计是为了在时间序列中处理数据，因此要求输入数据在第一个维度上具有时间依赖性（序列长度）。
• 批处理效率：通过 batch_size 维度，RNN可以同时处理多个样本，提高训练速度和资源利用效率。
• 灵活的输入：input_size 使得RNN可以适应不同维度的输入特征（例如，不同任务中词向量的维度）。

4.5、小结

理解输入数据的三维格式对于成功应用RNN至关重要。这种格式不仅确保了RNN能够处理和学习数据的时序信息，还能够提高模型在大型数据集上的计算效率。构建RNN模型时，确保数据的预处理步骤符合这一输入格式是关键的一步。