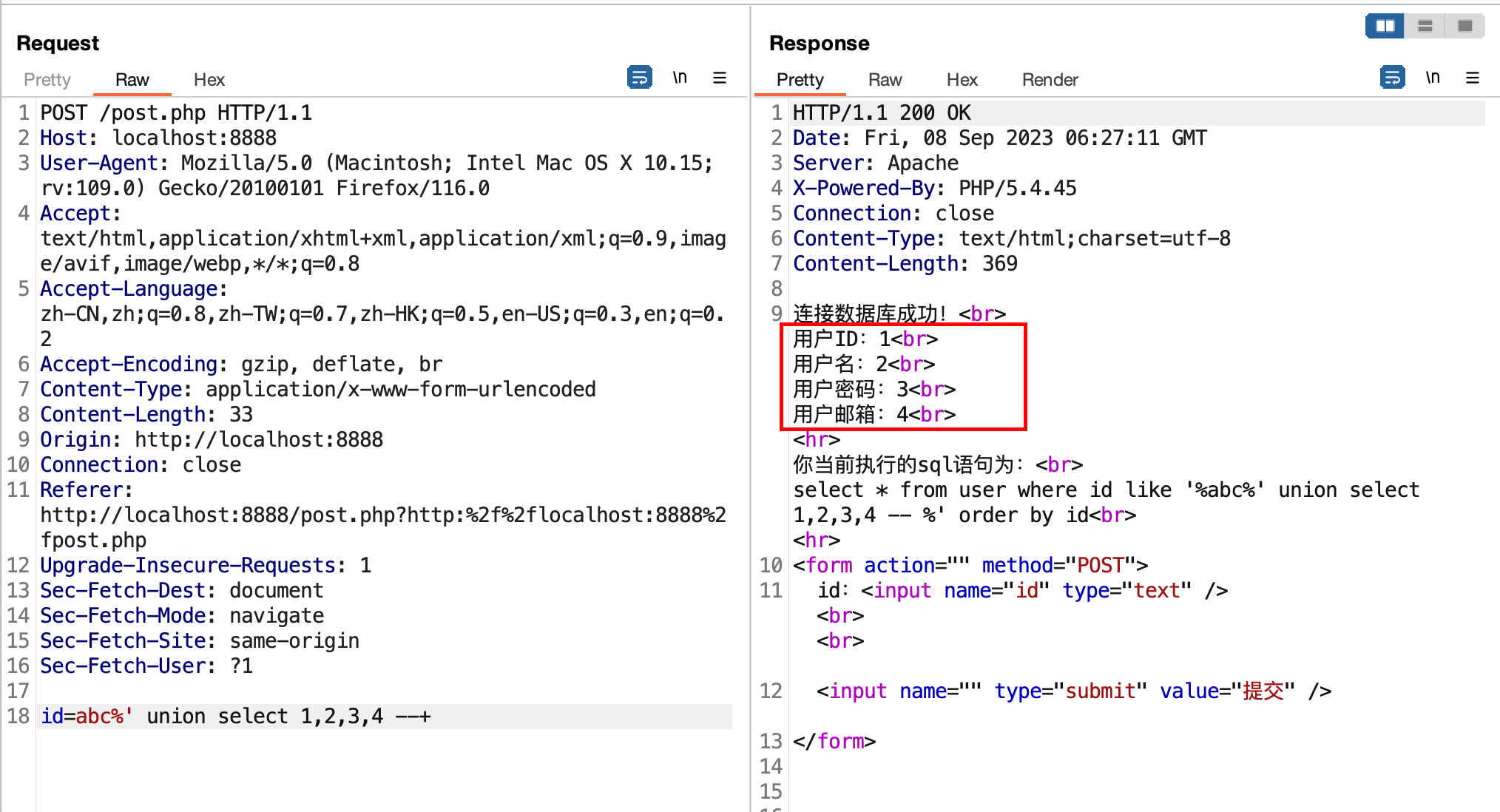
C++日常刷题积累
- 今日刷题汇总 - day028
- 1、游游的重组偶数
- 1.1、题目
- 1.2、思路
- 1.3、程序实现
- 2、体操队形
- 2.1、题目
- 2.2、思路
- 2.3、程序实现 -- 递归(dfs) + 剪枝
- 3、二叉树中的最大路径和
- 3.1、题目
- 3.2、思路
- 3.3、程序实现 -- 递归+树形dp
- 4、题目链接
今日刷题汇总 - day028
1、游游的重组偶数
1.1、题目

1.2、思路
读完题,知道让处理q组数据,让其重新排位,让这个数变成偶数,且不能有前导零,且重排后可与原数相等,如果重排后能成为偶数则输出,若无法成为偶数,则输出-1即可。那么,这个问题就成为如何判断偶数的问题,第一个方式就是判断这个数能够被2整除,第二个方法判断个位上的数是不是偶数即可。此外,由于我们老实的输入数字去摸得到每一位上的数比较麻烦,所以这里就利用string转数字提取每一位即可,再然后还有一些细节需要注意处理,那么接下来,就是程序实现。
1.3、程序实现
首先,按照思路和题目要求利用string输入每一组的数据number,然后遍历字符串如果是偶数就与最后的和个位交换,然后如果交换成功最后一位就是偶数,则满足条件,如果遍历完都没有执行交换说明就不是偶数,则输出-1。其中值得注意的细节就是,遍历选择从末尾开始遍历解决,这个数本身就是偶数如24时,然后如果从前遍历也会交换变成42,输出42与题目输出不匹配通过不了。所以就直接采用从末尾判断交换即可。
#include <iostream>
#include <string>
using namespace std;
int main()
{
int q;
cin >> q;
string number;
while (q--)
{
cin >> number;
int len = number.size();
int flag = 0;
for(int i = len - 1;i >= 0;i--)
{
if((number[i]-'0') % 2 == 0)
{
swap(number[i],number[len-1]);
flag = 1;
break;
}
}
if(flag)
cout << number << endl;
else
cout << -1 << endl;
}
return 0;
}

2、体操队形
2.1、题目

2.2、思路
读完题知道,就是让处理体操队员的排队问题,需要满足位置与队员需求,其中对于第 i 个队员的需求a[i]表示想要排在a[i]队员位置的前面,比如2号队员的需要a[3]表示想要排在a[2]位置,如果2号需求正好就是a[2]那么表示该队员没有位置需求,可任意分配即可。最后求满足所有队员的排队的方案有多少种?那么为了直观的理解画个图:

综上所述就是:根据题目中的队员位置需求与位置是否被占进行递归减治策略,采用dfs依次搜索合法位置就入队,知道所有队员全部放入即可。那么,接下来就是程序实现。
2.3、程序实现 – 递归(dfs) + 剪枝
根据思路分析的递归思想和减治策略实现,首先按照题目要求输入这里采用全局方便使用和输出结果,然后主要是完善dfs,这里同样是利用全局的特性,可以理解为直接一位一位的判断处理,所以主函数直接给第一个位置即可,然后dfs函数体中,如果当前位置越界那么就直接返回输出ret即可。其中题目中2 <= n <= 10;接着,遍历递归剩余位置,且利用bool vis数组判断队员是否已入队,且判断vis[arr[i]]队员的需求是否已经被满足了,如对于上图中第二个情况的第四组情况中,4号要求在2号前面,但是2号已经入队了就不满足,则都采用剪枝减去多余重复的操作,最后是合法的就进入标记,继续第二个位置递归。值得注意的是,执行恢复现场,因为上图思路分析中对于情况二发现到后面属于都不满足条件,无法有方案的,所以需要恢复到情况3的形式继续递归判断,搜索是否具有合法方案。
#include <iostream>
using namespace std;
const int N = 15;
int n,ret;
int arr[N];
bool vis[N];
void dfs(int pos)
{
if(pos == n+1)//说明遍历完,所有队员都合法入队
{
ret++;//方案+1
return;
}
for(int i = 1;i <= n;i++)
{
//剪枝
if(vis[i])//当前队员已入队了
continue;
if(vis[arr[i]])//当前队员的需求不满足,因为vis说明arr[i]需求的队员已经入队。
return;
//说明当前合法,则进行标记
vis[i] = true;
dfs(pos + 1);//继续下个位置
//注意:恢复现场,因为当前位置不合法时,需要将当前位置腾出来,才能让下一个队员进行递归判断
vis[i] = false;
}
}
int main()
{
cin >> n;
for(int i = 1;i <= n;i++)
cin >> arr[i];
dfs(1);
cout << ret << endl;
return 0;
}

3、二叉树中的最大路径和
3.1、题目

3.2、思路
读完题知道,二叉树里面的路径被定义为:从该树的任意节点出发,经过父=>子或者子=>父的连接,达到任意节点的序列。
注意:
1.同一个节点在一条二叉树路径里中最多出现一次
2.一条路径至少包含一个节点,且不一定经过根节点
那么给定一个二叉树的根节点root,请你计算它的最大路径和。
通过题目和示例分析,总结题目的概念就是一句话,就是将这棵树中画一条不会回溯的路线,求路线中最大路径和。如图:

那么由于路径是不定长且存在负数的情况,思考和分析以下几个要点:
(1)、要明白如何遍历树更适用?采用后序遍历,由左右子树汇集根节点更方便统计;
(2)、由于不不能回溯的所以这里的左右子树的路径和,实际上是一条单链和;
(3)、返回分为四种情况:
a、左右子树都是正数,则左+右+根的总和为最大路径和;
b、左子树和为负数,右子树和为正数,则返回右子树的和 + 根的和与只要右子树的路径相比的最大值,即max(右+根,右);因为根结点的值可能为负数;
c、同理,左子树和为正数数,右子树和为负数,则max(左+根,左);
d、左右子树都为负数,则返回与根结点的比较,max(根,max(左,右));
接下来,就是程序实现。
3.3、程序实现 – 递归+树形dp
综上所述总结为树形dp:
a. 左⼦树收集:以左⼦树为起点的最⼤单链和;
b. 右⼦树收集:以右⼦树为起点的最⼤单链和;
c. 根节点要做的事情:整合左右⼦树的信息,得到经过根节点的最⼤路径和;
d. 向上返回:以根节点为起点的最⼤单链和
class Solution
{
public:
int ret = -1010;
int dfs(TreeNode* root)
{
if (root == nullptr)
return 0;
int left = max(0, dfs(root->left));// 左⼦树的最⼤单链和,max 0去除负数
int right = max(0, dfs(root->right)); // 右⼦树的最⼤单链和
// 经过root的最⼤路径和
ret = max(ret, root->val + left + right);
return root->val + max(left, right);
}
int maxPathSum(TreeNode* root)
{
dfs(root);
return ret;
}
};


4、题目链接
🌟游游的重组偶数
🌟体操队形
🌟二叉树中的最大路径和