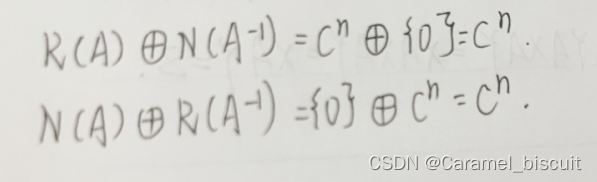
1. A为正规矩阵时，A的奇异值是A的特征值的模。
2. A为半正定Hermite矩阵时，A的奇异值是A的特征值。

最佳逼近解
最小二乘解

矩阵的单边逆

A是左可逆的充要条件是A为列满秩矩阵

A是左可逆的充要条件是NA={0}

投影矩阵N(A)=R(I-A),N(I-A)=R(A)

A是右可逆的充要条件是R(A)=C^m

求A的一个左逆矩阵

求A的一个右逆矩阵

单边逆矩阵不唯一

左逆矩阵与求解方程组Ax=b之间的关系

右逆矩阵与求解Ax=b之间的关系

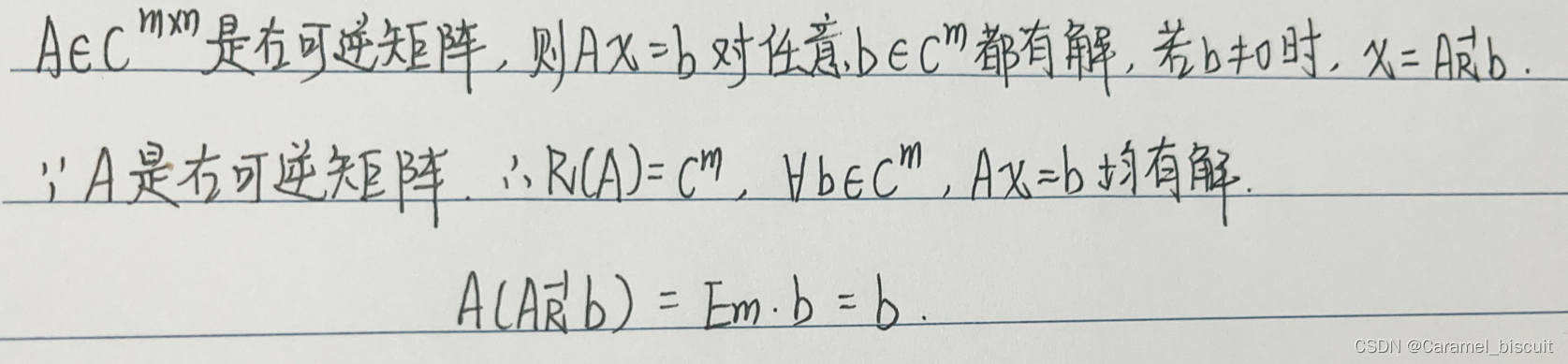
可逆矩阵相乘不改变矩阵的秩

广义逆矩阵

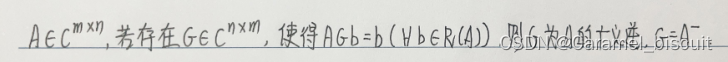
广义逆矩阵不唯一

G为广义逆矩阵的充要条件AGA=A

广义逆矩阵的秩大于等于矩阵的秩

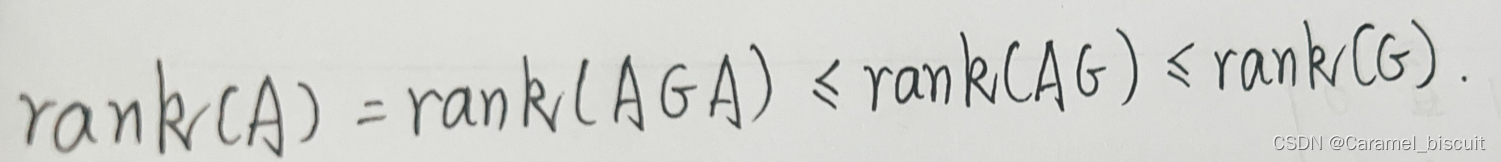
广义逆矩阵的性质

1. 矩阵的转置的广义逆=矩阵的广义逆的转置
   
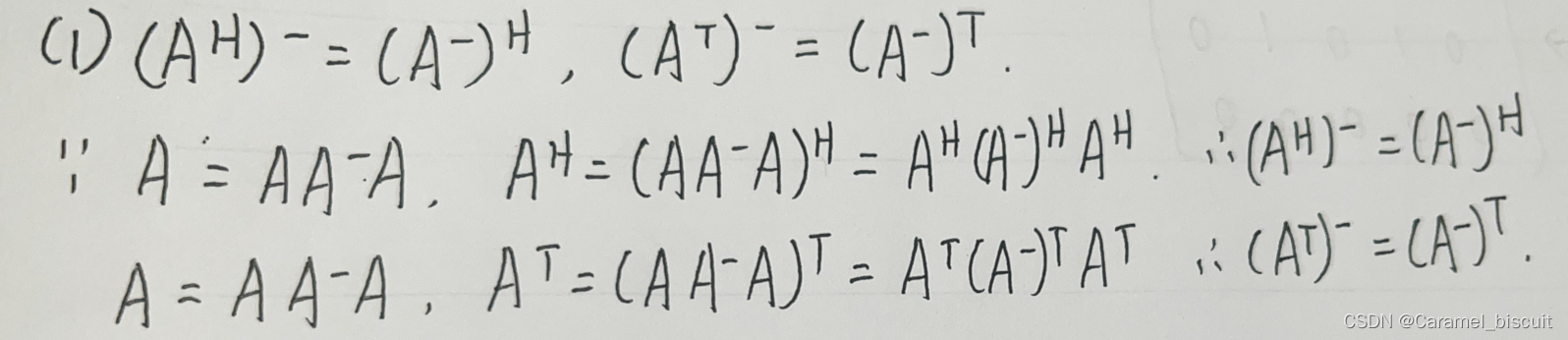
2. 矩阵与其广义逆矩阵的乘积为幂等矩阵，且秩相等
   
3. 特征值与广义逆
   
4. 广义逆矩阵的构造
   
5. R(AA^-)=R(A) N(A^-A)=N(A)
   
6. 广义逆与投影
   

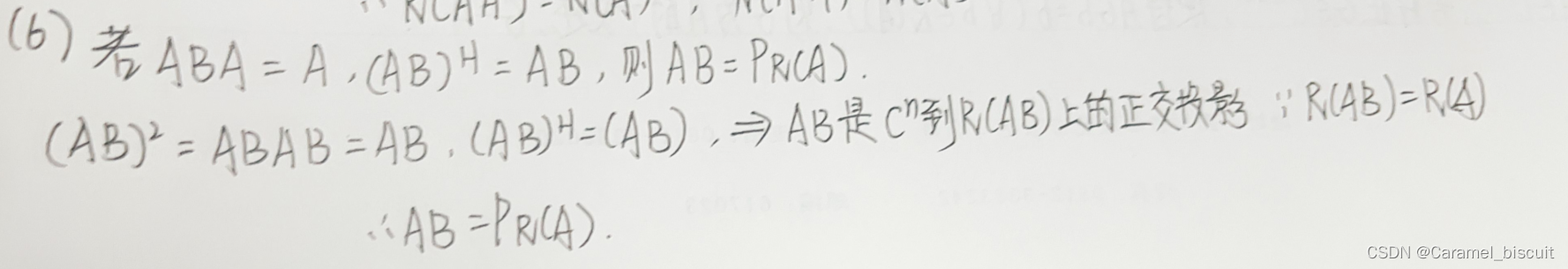
rank(A)=n的充要条件是A^-A=En

自反广义逆矩阵

A的自反广义逆矩阵是同时满足Pernose第一、二两个矩阵方程


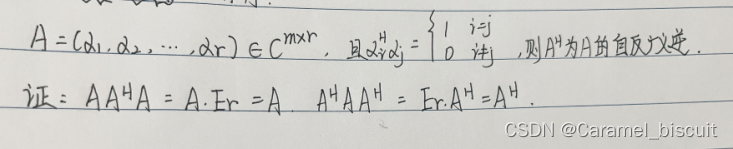
A是行满秩矩阵，则A的右逆矩阵也是A的自反广义逆矩阵。

任何矩阵都有自反广义逆。

自反广义逆矩阵比单边逆矩阵更具有一般性（因为单边逆有时不存在）
自反广义逆不是唯一的

构造自反广义逆

A的自反广义逆一定是A的广义逆，而A的广义逆不一定是A的自反广义逆。

下列任意两个等式成立都能推出第三个等式成立。

1. rank(A) = rank(X)
2. AXA = A
3. XAX = X

当A是可逆矩阵时，A的值域和零空间的关系